Чем отличаются картографические проекции друг

НАВИГАЦИЯ. Глава 3. §19 Классификация картографических проекций.

§19 Классификация картографических проекций.

Картографические проекции можно классифицировать по различным признакам. Однако с точки зрения построения и практического использования карт, наиболее употребительными признаками их классификации служат:

• характер искажений проекций, обусловливающий возможности практического использования карт;

• вид меридианов и параллелей нормальной сетки.

По характеру искажений

все картографические проекции делятся на четыре группы:

• равноугольные, или конформные;

• равновеликие, или эквивалентные (равноплощадные);

Равноугольные проекции

Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых фигур на карте соответствующим фигурам на поверхности Земли.

Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом.

Однако, при сохранении неискаженными углов и направлений, в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки.

Постоянство частного масштаба в данной точке по всем направлениям облегчает производство измерений на карте, составленной в равноугольной проекции. Для учета изменения масштаба при измерении больших отрезков их следует измерять на карте по частям.

Свойство конформности позволяет на картах, составленных в таких проекциях, измерять углы и азимуты непосредственно с помощью транспортира. Эти свойства обусловили широкое применение равноугольных проекций для построения морских карт. Отметим, что равноугольные проекции сохраняют равными углы, но не кривизну линий, поэтому подобие сохраняется только для малых фигур.

К равноугольным проекциям относятся проекции Меркатора, Гаусса, стереографическая и некоторые другие.

Равновеликие проекции

Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте.

Бесконечно малый на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе.

На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.

Равнопромежуточные проекции

Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных направлений.

Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга.

Произвольные проекции

Проекции, не относящиеся ни к одной из рассмотренных групп, но обладающие какими-либо другими, важными для практики свойствами, называются произвольными.

К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.

По виду меридианов и параллелей нормальной картографической сетки

проекции делятся на следующие основные группы:

Из всех перечисленных здесь рассматриваются лишь те виды проекций, которые используются или могут использоваться для построения морских карт.

Конические проекции

Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов.

Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса.

Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса. т. е. меньше главного масштаба.

Азимутальные проекции

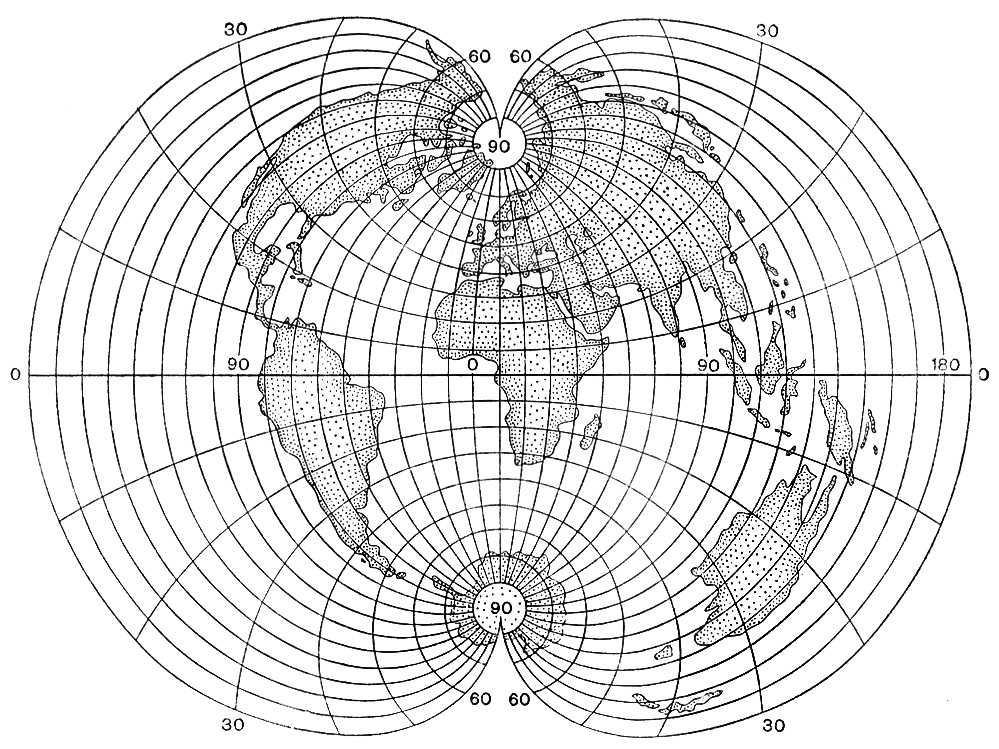
Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов

Из приведенного определения видно, что азимутальные проекции являются частным случаем конических проекций.

Точка схождения меридианов в азимутальных проекциях является изображением полюса нормальной системы координат. Свойствами азимутальных проекций являются: равноугольность, равновеликость или равнопромежуточность.

К классу азимутальных проекций относятся перспективные проекции, получающиеся путем проектирования точек поверхности глобуса (шара) на картинную плоскость лучами, исходящими из постоянной точки.

Эта точка называется точкой зрения.

Картинная плоскость может или касаться поверхности проектируемого глобуса, или находиться от него на некотором удалении, или пересекать ее. Точка зрения выбирается на перпендикуляре к картинной плоскости, проходящем через центр проектируемого глобуса.

В зависимости от расположения точки зрения относительно центра глобуса перспективные проекции делятся:

— на ортографические, когда точка зрения удалена в бесконечность;

— на внешние, когда точка зрения находится на конечном расстоянии от центра проектируемого глобуса, но далее точки, представляющей антипод полюса нормальной системы координат;

— на стереографические, когда расстояние от центра глобуса до точки зрения равно радиусу глобуса, т.е. когда точка зрения помещается в точке шара, противоположной полюсу нормальной системы координат (в точке — антиподе полюса нормальной системы координат);

— на центральные (гномонические), когда точка зрения помещена в центре глобуса.

Цилиндрические проекции

Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых изображаются взаимно перпендикулярными прямыми.

Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот.

Общие уравнения цилиндрических проекций имеют вид:

x = f (φ); y = C λ

Вид функции x = f (φ) и коэффициент С определяют важнейшие свойства цилиндрической проекции. Изменяя их, можно получить равноугольную, равнопромежуточную, равновеликую или произвольную проекцию. Цилиндрические проекции могут быть получены путем проектирования поверхности глобуса на касательный или секущий глобус цилиндр. При проектировании на касательный по экватору цилиндр масштаб вдоль экватора сохраняет равенство главному масштабу, т.е. экватор глобуса изображается на проекции без искажений. При проектировании на секущий цилиндр линиями нулевых искажений будут являться параллели сечения.

Из цилиндрических наиболее употребительны в кораблевождении прямая и поперечная проекции Меркатора и поперечная проекция Гаусса.

Источник

Ликбез по картографическим проекциям с картинками

Визуализация данных самого разного рода, имеющих некое географическое распределение, в последнее время получает все большее и большее распространение. Тут, на Хабре, статьи с картами встречаются чуть ли не каждую неделю. Карты в статьях очень разные, но роднит их одно: как правило, в них используются всего две картографические проекции, при том — не самые удачные из существующих. Мне бы хотелось дать несколько наглядных примеров проекций, которые выглядят более эстетично и лучше приспособлены для разных видов визуализации. В этой статье будут рассмотрены общемировые проекции и проекции большей части Земли, так как визуализация чего-либо на карте мира, пожалуй, является наиболее распространенной из подобных задач.

Легкое введение

Поскольку статья ориентирована на вопросы визуализации данных, я не буду касаться глубоко теории проекций (датумов, конформности, равноугольности и тому подобного), кроме общих принципов их построения. Также, я буду говорить тут о «проекциях», формально подразумевая «систему координат», coordinate reference system, потому что для карт таких масштабов не имеет смысла отдельно рассматривать проекцию и датум. Математики здесь тоже практически не будет, кроме простой геометрии. Желающие ознакомиться с математическими принципами, могут это сделать по статьям на Wolfram MathWorld. Так что изучающим программирование в области геоинформационных систем или их опытным пользователям, эта статья, возможно, будет не очень полезна.

Перед началом, объясню пару вещей. Все примеры будут даваться с использованием набора данных государственных границ с вот этого сайта и набора данных Blue Marble Next Generation с сайта NASA. Последний включает в себя синтезированные безоблачные снимки земной поверхности за каждый из двенадцати месяцев 2004-го года, что позволит внести некоторое разнообразие в иллюстрации.

Я очень люблю открытый софт, но использовать GDAL в данном случае мне показалось неэффективно — некоторых не очень ходовых, но полезных проекций в его реализации на данный момент либо нет, либо я плохо смотрел исходники, а потому иллюстрации я готовил в коммерческой программе GlobalMapper, которой пользуюсь уже много лет, и которая славится поддержкой внушительного списка систем координат.

Названия проекций и некоторые термины я буду давать и англоязычные, потому что если кому-то захочется поискать материалы по этой теме, русскоязычных источников в сети найдется несколько меньше (объем статей в Википедии на русском меньше в несколько раз). Для большинства проекций я постараюсь дать не только названия, но и коды EPSG и/или WKID, а также название проекции в библиотеке PROJ.4, широко используемой в открытом софте (например, в пакете R) для поддержки систем координат.

Некоторые проекции, возможно, окажутся кому-то знакомыми по картинке с xkcd, но все из них тут рассмотрены не будут.

Проблема

Начнем с того, что же это за самые распространенные проекции, и что с ними не так.

Первая проекция — так называемая «Географическая», она же – Geographic projection, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго говоря, она даже не совсем является проекцией, потому что получается путем интерпретации полярных угловых координат, как линейных прямоугольных, без всяких вычислений. Эту проекцию используют, потому что она способна отобразить всю поверхность Земли целиком и потому, что она самая простая математически, а данные очень часто распространяются не спроецированными, то есть именно в географических координатах (градусах широты и долготы).

Другая весьма популярная проекция — «проекция Меркатора», Mercator projection PROJ.4:merc. Она также используется для визуализации данных, покрывающих весь мир, но ее популярность продиктована не только простотой — ее варианты являются стандартом де-факто для глобальных картографических сервисов, таких как Google Maps, Bing Maps, Here. С ней глубоко связаны картографические библиотеки OpenLayers, Leaflet, API упомянутых выше сервисов. В варианте Google и OpenStreetMap она носит название Web Mercator и имеет код EPSG/WKID:3857, иногда на нее также ссылаются, как на EPSG:900913. Принцип ее построения не сильно сложнее Географической – это проекция на цилиндр, чья ось совпадает с географической осью Земли, проецирование происходит линиями, выходящими из центра планеты, от чего ошибка растяжения приполярных областей по горизонтали оказывается скомпенсирована пропорциональным растяжением по вертикали. Проблема с этим только в том, что карта получится слишком большой по вертикали, если попытаться отобразить и север Гренландии. Потому обычно отбрасывают 16° полярных областей (в равной пропорции или больше — с юга).

На чей-то взгляд выглядит чуть лучше, чем Географическая, но одну проблему мы уже упомянули, а вторая — чем ближе объект к полюсам, тем он кажется больше, хотя его форма уже не так искажена. Потому, если предмет визуализации — плотность маркеров на единицу территории или расстояния, такой способ отображения будет вводить в заблуждение. При грамотном выборе способа визуализации, конечно, это можно скомпенсировать, а для каких-то случаев это вообще не проблема: например, если величина какого-то показателя в целой стране соотнесена с цветом этой страны на карте, эффект растяжения площадей не сказывается. Эта проекция сохраняет только форму объектов, потому очертания континентов и стран выглядят довольно узнаваемо. И, как я уже сказал, она — ваш первый и самый простой вариант при создании интерактивных веб-карт.

Варианты решения

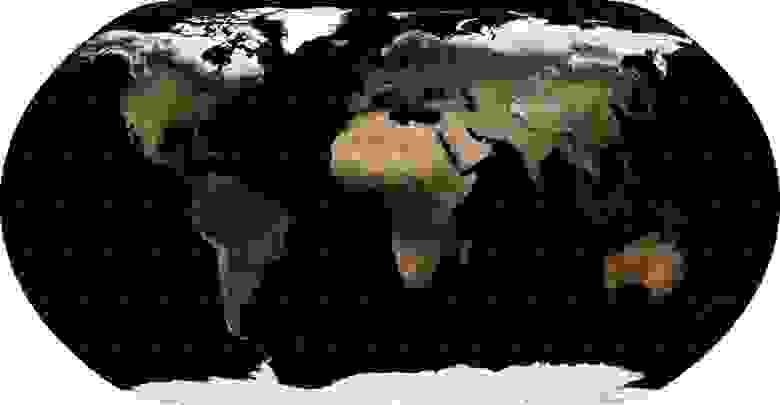
Что же делать с глобальными данными, если нам по какой-то причине понадобилась проекция, лучше сохраняющая такие свойства объектов, как форма, площадь, расстояния и углы? Законы геометрии не дают нам сохранить все эти свойства сразу, развернув круглую поверхность Земли на плоскость. Однако, для визуализации данных более всего важна эстетика и восприятие, а не сохранение свойств, как для навигационных или измерительных задач. Потому становится возможным подобрать такую проекцию, искажения в которой были бы равномерно распределены по свойствам. И таких проекций существует довольно много. Существуют три самых известных, обладающих сходными свойствами: «Тройная проекция Винкеля» Winkel Tripel WKID:54042 PROJ.4:wintri, «проекция Робинсона» Robinson projection WKID:54030 PROJ.4:robin, «проекция Каврайского» (Kavrayskiy projection). Первая и последняя имеют визуально минимальные искажения, а неспециалисту, не видя градусной сетки, вообще весьма сложно различить их, потому я приведу иллюстрацию для Winkel Tripel, как той, которая лично мне нравится больше всего.

Вот так описание этой проекции выглядит в формате ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,0],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]

Как легко видеть, хотя искажение контуров и некоторое увеличение площади стран к полюсам здесь также наблюдаются, но это нельзя даже сравнивать с растяжением Географической проекции и пропорциональным увеличением проекции Меркатора.

Тут стоит сделать небольшое отступление и обратить внимание на то, что вид этой проекции по умолчанию страдает одним недостатком, который касается и других общемировых проекций. Дело в том, что если за центральный меридиан — линию, соединяющую северный и южный полюс через центр карты (longitude of origin) — принять нулевой меридиан, то карта будет разрезана по 180-му. Но при этом треть Чукотки окажется на левом краю карты, а две трети — на правом. Чтобы сделать карту красивее, разрез должен проходить где-то в районе 169-го западного меридиана восточнее острова Ратманова, для чего за центральный должен быть принят 11-й. Вот иллюстрация того, что получается:

А вот измененное для этого случая описание в ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,11],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]

В формате определения системы координат для PROJ.4 долгота центра проекции задается параметром +lon_0=.

11-й меридиан — «магическое» число: практически все мировые проекции, имеющие равномерный масштаб вдоль экватора, могут быть разрезаны по Берингову проливу, если за центральный принять именно его, а не нулевой.

Замечу, что задумываясь о выборе проекции, стоит принимать во внимание все существующие реальные требования к визуализации. Например, если данные касаются климата, то может иметь смысл либо нанести на карту линии широты, либо использовать проекцию, где они горизонтальны, а не загибаются к краям карты (то есть, отказаться от Тройной Винкеля в пользу, например, Робинсона). В данном случае, это позволит легче и точнее оценить относительную близость разных мест к полюсам и экватору. Еще один весомый плюс проекции Робинсона — то, что она поддерживается множеством софта, в том числе открытого, тогда как про некоторые другие этого сказать нельзя.

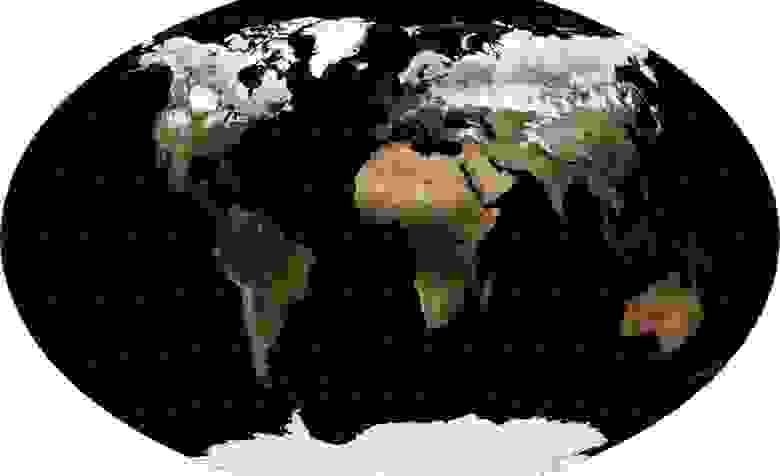
Иногда, когда требуется максимально сохранить какое-то свойство, например — соотношение площадей объектов (стран) — эстетическая сторона страдает. Но поскольку это все же может для чего-то понадобиться, я приведу один пример такой проекции — «проекцию Моллвейде», Mollweide projection WKID:54009 PROJ.4:moll.

Как видно, она довольно сильно напоминает проекцию Робинсона, но с той разницей, что полюса все же стянуты в точки, от чего форма приполярных областей выглядит сильно искаженной. Но пропорции площадей стран, как и требовалось, сохраняются куда лучше.

Самым молодым конкурентом этих проекций является проекция Natural Earth PROJ.4:natearth — она представляет из себя гибрид проекций Каврайского и Робинсона, а ее параметры были подобраны группой американских, швейцарских и словенских специалистов в 2007 году, тогда как возраст большинства картографических проекций — не менее полувека.

Для перепроецирования данных в нее существует некоторое количество инструментов, которые были написаны специально для этого, но ее поддержка еще далека от повсеместной.

Немного экзотики и специальных случаев

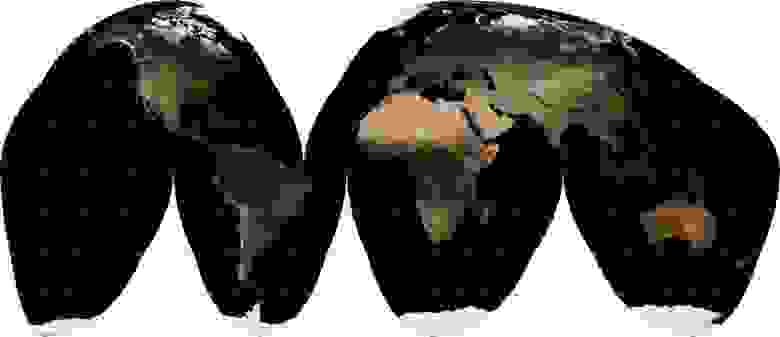
Конечно, все многообразие проекций на этом не заканчивается. Их изобретено немало. Некоторые просто выглядят странно (скажем, проекция Бонне изображает Землю в виде фигуры, напоминающей разрезанное яблоко или стилизованное сердце), некоторые — предназначены для особых ситуаций. Например, готов поспорить, что очень многие видели на картинках карту мира, которая похожа на корку мандарина, которую сняли и расплющили. Это, наверняка, была «Разрывная гомолосинусоидальная проекция Гуда» Interrupted Goode Homolosine projection WKID:54052.

Вид ее вполне достоин названия. Ее назначение — отображать размер объектов (и в некоторой степени — форму) близко к естественным пропорциям. Ее главная проблема, кроме названия и странного вида, состоит в том, что путем подбора центрального меридиана невозможно добиться того, чтобы ни один крупный кусок суши не был разрезан. Обязательно пострадает что-то из списка: Гренландия, Исландия, Чукотка, Аляска. Лично на мой взгляд, проще привести отдельно изображения стран, чем использовать такую карту, если вы не хотите стилизовать свою работу под середину XX века.

На иллюстрации эта проекция имеет широту и долготу центра, равные широте и долготе Москвы, а высоту — 5000000 метров. Чем больше это расстояние, тем сильнее изображение Земли становится похоже на ее изображение в проекции, которую мы рассмотрим последней.

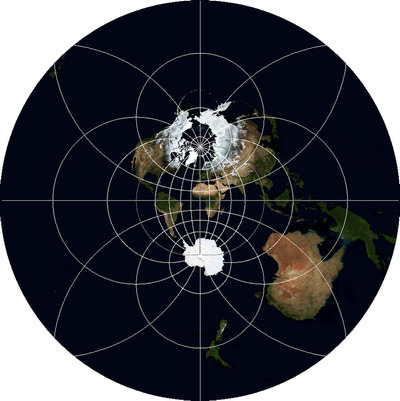
Проекция, которая показывает вид на Землю в параллельной перспективе, то есть как-бы с бесконечного расстояния, называется «Ортографическая проекция» Orthographic projection WKID:43041 PROJ.4:ortho. В каком-то смысле, она знакома всем, кто когда-либо пользовался Google Earth. Я говорю, что в каком-то смысле, потому что «направление взгляда» в этой проекции всегда перпендикулярно поверхности Земли, тогда как в Google Earth его можно наклонять как угодно.

Для нее, как и для предыдущей проекции, можно задать центральные широту и долготу, чтобы ориентировать Землю желаемым образом. Например, можно показать полушарие с центром в какой-то точке, о которой идет речь — скажем, иллюстрируя транспортные потоки континентального масштаба, исходящие от одного предприятия. Сделав две карты с противоположными значениями координат, можно получить карту всего мира (правда, на краях искажения будут очень велики). Генерация последовательности карт с плавным изменением центральной точки даст кадры для анимации вращающейся планеты без всякой трехмерной графики.

Если статья окажется интересной, постараюсь написать продолжение о проекциях, используемых для отображения отдельных стран или регионов, ориентированную, как и эта статья, на базовые свойства этих проекций для задачи визуализации данных, инфографики и тому подобного.

Источник

Чем отличаются картографические проекции друг от друга

Картографическая проекция – это математически определенный способ изображения поверхности эллипсоида на плоскости, устанавливающий аналитическую зависимость между географическими координатами точек земного эллипсоида и прямоугольными координатами тех же точек на плоскости. Друг от друга они могут отличаться по характеру искажений, виду нормальной сетки или по ориентировке геометрической поверхности по отношению к элементам земного эллипсоида. Попробуем разобраться, в чем разница между картографическими проекциями подробнее.

По характеру искажений проекции делятся на равноугольные, равновеликие и произвольные. Первые можно выявить по отсутствию искажений углов и форм бесконечно малых фигур на карте. Масштаб длин в каждой точке постоянен по всем направлениям и зависит только от положения точки. Эллипсы искажений – окружности, увеличивающие радиус по мере удаления от места нулевых искажений. Равновеликие проекции отличаются тем, что на карте искажения площадей отсутствуют. Увеличение масштаба длин по одной оси эллипса искажений компенсируется уменьшением масштаба длин по другой оси, что вызывает сильное искажение углов и форм. Произвольные картографические проекции имеют искажения и углов, и площадей. Однако искажений углов в них меньше, чем в равновеликих, в то время как искажение площадей меньше, чем в равноугольных.

По виду вспомогательной геометрической поверхности различают цилиндрические, конические и азимутальные проекции. Картографические проекции первого вида характеризуются тем, что сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного или секущего цилиндра, затем цилиндр разрезается по образующей и развертывается в плоскость. В зависимости от ориентировки цилиндра относительно земной оси цилиндрические проекции бывают нормальными, косыми и поперечными. Конические картографические проекции характеризуются тем, что в них сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного или секущего конуса, затем конус разрезается по образующей и развертывается в плоскость. В зависимости от ориентировки конуса относительно земной оси их делят также на нормальные, косые и поперечные. Косые и поперечные конические проекции встречаются очень редко. Азимутальными называют картографические проекции, в которых сеть параллелей и меридианов переносится с поверхности эллипсоида на касательную (или секущую) картинную плоскость. Точка касания плоскости и земного эллипсоида является точкой нулевых искажений. Делят такие проекции в зависимости от положения точки касания на простые и перспективные.

Выводы:

Источник