Чем отличаются графики функций

Построение графиков функций

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

x	y
0	-1
1	2

x	y
0	2
1	1

x	y
0	0
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Сдвигаем график вправо на 1:

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Источник

Чем отличается график функции от графика производной

Знание — сила. Познавательная информация

График производной функции

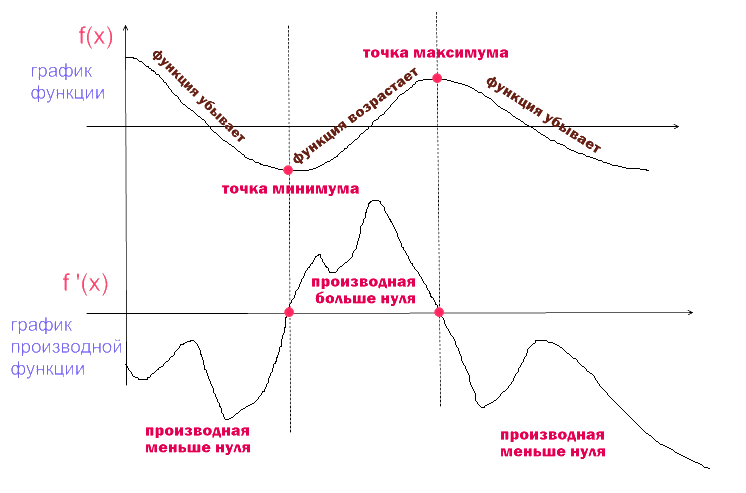
Задания, в которых на рисунке изображен график производной функции y=f ‘(x), и нужно определить точки экстремума и промежутки монотонности функции y=f(x), решаются очень просто.

Достаточно помнить, что

1) функция y=f(x) возрастает на промежутках, где производная y=f ‘(x)>0;

2) функция y=f(x) убывает на промежутках, где производная y=f ‘(x) внутренних точек области определения, то есть точки на концах области определения не рассматриваем);

4) функция y=f(x) имеет точки экстремума там, где производная y =f ‘(x) меняет свой знак.

В частности, функция y=f(x) имеет точки максимума там, где производная меняет знак с плюса на минус;

функция y=f(x) имеет точки минимума там, где производная меняет знак с с минуса на плюс.

На рисунке изображен график производной функции. С помощью графика найти промежутки монотонности функции, критические точки, критические точки и точки экстремума.

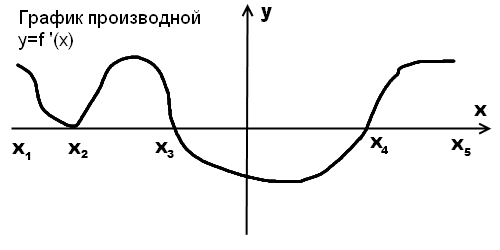
рис.1. По графику производной исследовать функцию.

Функция y=f(x) возрастает на промежутках (x1;x3) и (x4;x5) (то есть там, где производная y=f ‘(x) положительна, а значит, ее график расположен выше оси оx). Точку x2 не исключаем из промежутка возрастания — производная в этой точке равна нулю, но знак не меняет.

Функция y=f(x) убывает на промежутке (x3;x4) (то есть там, где производная y=f ‘(x) отрицательна, а значит, ее график расположен ниже оси оx).

Критические точки: x2, x3, x4. В этих точках производная обращается в нуль (а график производной, соответственно, пересекает ось ox).

x=x3 — точка максимума функции y=f(x), поскольку производная y=f ‘(x) в этой точке меняет знак с плюса на минус (график производной пересекает ox в направлении сверху вниз).

x=x4 — точка минимума функции y=f(x), так как производная y=f ‘(x) в этой точке меняет знак с минуса на плюс (график производной пересекает ox в направлении снизу вверх).

Точки экстремума: x3 и x4. В них производная не только обращается в нуль, но и меняет свой знак. Точка x=x2 — критическая, но точкой экстремума не является поскольку нет смены знака производной. То есть точки экстремума на графике производной — это те точки в которых график не касается, а пересекает ось ox.

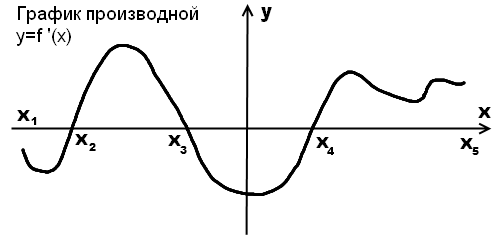
рис.2. По графику производной исследовать функцию

Функция y=f(x) возрастает на промежутках (x2;x3) и (x4;x5).

Функция y=f(x) убывает на промежутках (x1;x2) и (x3;x4).

Критические точки: x2, x3, x4.

Точка максимума — x=x3.

Точки минимума — x=x2 и x=x4.

С помощью графика производной y=f ‘(x)также можно сравнивать значения функции y=f(x). Такие задания рассмотрим позже.

9 комментариев на «График производной функции»

Неплохо, все просто и понятно!

Превосходно!
Напишите пожалуйста аналогичную статью о второй производной!

Спасибо!
Постараюсь о второй производной написать на следующей неделе.

Рассмотрим и сравним график функции и ее производной (рис.1)

Рисунок 1. График производной

Свойства графика производной

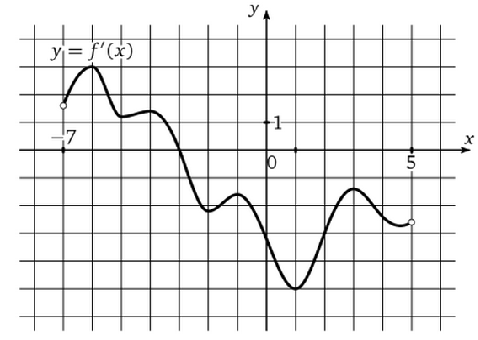
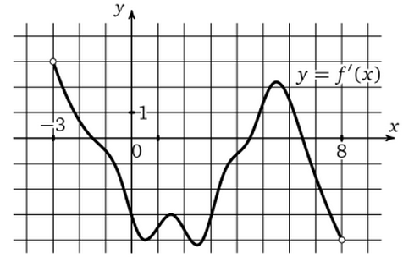
По графику (рис.2) производной определить, в какой точке на отрезке [-3; 5] функция максимальна.

Рисунок 2. График производной

Попробуй обратиться за помощью к преподавателям

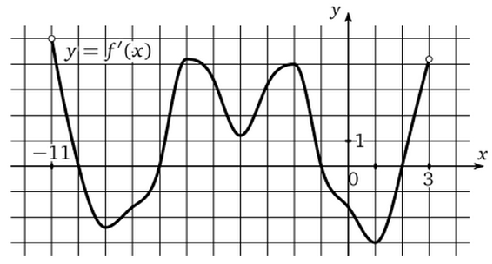
По графику (рис.3) производной определить количество точек максимума на отрезке [-11; 3].

Рисунок 3. График производной

По графику (рис.3) производной определить количество точек экстремума.

Решение: Экстремумом являются точки как минимума, так и максимума. Найдем количество точек, в которых производная меняет знак:

Функция содержит 4 экстремума.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

По графику (рис.4) производной определить количество целых точек на промежутке убывания.

Рисунок 4. График производной

Решение: Интервалам убывания соответствуют (-3,-1.5) и (4.5,6.5). Количество целых точек по прямой х: 2(на первом промежутке) и 2 (на втором промежутке).

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Производная характеризует скорость изменения функции Если функция возрастает – производная положительна (касательная наклонена вправо) Если функция убывает – производная отрицательна (касательная наклонена влево) Если функция имеет максимум или минимум, либо «точку перегиба» – производная равна нулю (касательная лежит горизонтально) Чем больше скорость возрастания (или убывания) функции, тем больше по модулю производная, и тем круче (ближе к вертикали) наклон касательной В точках А и D функция возрастает – производная положительна. В точке А наклон касательной круче, значит, и производная больше, чем в точке D. В точках В и С функция убывает – производная отрицательны. В точке В функция наклон касательной круче, значит, производная меньше, чем в точке C (ПО МОДУЛЮ – больше)

Геометрический смысл производной

Производная – это тангенс угла наклона касательной (или угловой коэффициент касательной)

Как найти угловой коэффициент касательной (или производную)

Пример: На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .

1. Найти точки на линии касательной, которые точно попадают в пересечение клеточек (обычно на рисунке эти точки отмечены).

2. Через одну из точек провести горизонтальную линию, через другую – вертикальную. Получится треугольник.

3. Сосчитать (в клеточках) длины вертикальной и горизонтальной сторон треугольника. Разделить длину вертикалной стороны на длину горизонтальной

4. Если наклон касательной вправо («подъем») – ставим знак «плюс», если наклон влево («спуск») – ставим знак «минус»

Вертикаль: 2 клетки Горизонталь: 8 клеток Здесь «подъем», знак «плюс».

Ответ: Значение производной в точке х равно 0,25

Нахождение точек, где касательная параллельна прямой

Если требуется определить точки, где касательная параллельна прямой , то надо искать точки, где производная равна k (числу перед иксом). А если касательная должна быть параллельна прямой (или оси абсцисс), то производная должна быть равна 0)

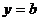
Пример: Дан график производной функции f(x). Указать количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=x Решение: для прямой y=x угловой коэффициент равен 1, значит, производная должна быть равна 1. Таких точек на графике две.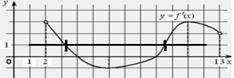

Физический смысл производной

Пример: Материальная точка движется по закону 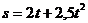. Найти мгновенную скорость в момент

Скорость v – производная от перемещения s: 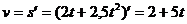. При t=5

Связь графиков функции и производной

Производная	Функция	Касательная к графику функции
Положительна	Возрастает	Наклонена вправо (острый угол с осью Х)
Отрицательна	Убывает	Наклонена влево (тупой угол с осью Х)
Равна нулю (с вариантами)	Стационарная точка

Горизонтальна (параллельна оси Х)

=0, меняет знак с мИнуса на плюсМинимум (экстремум)=0, меняет знак с плюСа на минусМакСимум (экстремум)=0, но знак не меняетТочка перегиба

Дата добавления: 2018-06-01 ; просмотров: 1093 ; ЗАКАЗАТЬ РАБОТУ

Источник

Функции и графики

Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике – функции полезности, издержек, функции спроса, предложения и потребления. в радиотехнике – функции управления и функции отклика, в статистике – функции распределения. Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций». и/или по ссылке Построение графиков, содержащих модуль аргумента или модуль функции, а также сумму или разность нескольких модулей.

С 17.04.21 до экзаменв просмотр по кнопке ОТКРЫТ.

В школьном курсе математики изучаются следующие
элементарные функции.

Степеннаяy = x 3Кубическая параболаСамый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Движение графиков функций».Степеннаяy = x 1/2График функции
y = √xСамый простой случай для дробной степени (x 1/2 = √x). Случаи с коэффициентами изучаются в разделе «Движение графиков функций».Показательнаяy = a xГрафик показательной функцииПоказательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5 x (a = 1/2 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log₂x (a = 2 > 1).Логарифмическаяy = log_axГрафик логарифмической функцииЛогарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log_0,5x (a = 1/2

На сервере youtube.com открыт канал Mathematichka, на котором размещаются видео, связанные с изучением графиков функций и экзаменационными задачами на эту тему. Подписывайтесь и пишите в комментариях свои вопросы и пожелания.

Пример такого видео.

Перейти на главную страницу.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

Источник