Чем отличаются числовые и буквенные выражения
Числовые и буквенные выражения. Порядок действий.
теория по математике 📈 алгебраические выражения
Числовое выражение – это выражение, состоящее из чисел и знаков действий, а также скобок.
Пример №1. В каждом из этих выражений содержатся числа, между которыми есть знаки действий, а также бывают скобки. Это и есть числовые выражения.
Если выполнить по порядку все действия, которые есть в числовом выражении, то получится определенное число, которое называют значением числового выражения. Порядок действий в числовых выражениях определяется правилами.
Действия сложение и вычитание принято называть действиями первой ступени, а умножение и деление – действиями второй ступени. Возведение в степень – это действие третьей ступени.
Порядок действий в выражении, не содержащем скобки
890 – 567 + 2340 – 124
в данном выражении действия одной ступени (сложение и вычитание), поэтому выполняем их по порядку слева направо:
в этом выражении также действия одной ступени (умножение и деление), поэтому выполняем их по порядку слева направо:
здесь присутствуют действия всех ступеней. Поэтому начинаем выполнять их с наивысшей ступени – возведения в степень. Затем слева направо выполняем деление и умножение, а затем слева направо – сложение и вычитание:
Порядок действий в выражении, содержащем скобки
Если числовое выражение содержит скобки, то выполняют сначала действия в скобках, следуя правилу, а затем – действия за скобками.
(3245 + 67,92:2)×3 + (126×2 – 321:3) – 125
здесь числовое выражение содержит скобки, поэтому действия выполняем в скобках слева (деление, затем сложение), затем в скобках справа (умножение, деление, вычитание):
Теперь выполняем действия за скобками слева направо (умножение, сложение, вычитание):
Буквенные выражения. Числовое значение буквенного выражения.
Выражения, содержащие не только числа и знаки действий, но и буквы, называют буквенными. Буквы также можно называть «переменная». Обращаем внимание на то, что знак «умножить» между числом и буквой не пишется.
Пример №6. Примеры буквенных выражений:
Числовое значение буквенного выражения – это значение числового выражения, полученного при подстановке конкретных значений переменной в данное выражение.
Пример №7. Найдем значение выражения с + х при с=23, х=0,17. Для этого подставим вместо с и х их данные числовые значения и получим числовое выражение 23 + 0,17. Теперь вычислим результат и получим 23,17. Таким образом, числовое значение буквенного выражения с + х равно 23,17.
Пример №8. Н айдем значение выражения 11х +(с — d) при х=10, c=178, d=121. Для этого подставляем вместо каждой переменной соответствующие числовые значения и получим числовое выражение 11×10 + (178 – 121). Выполнив действия, получим ответ 167. Это и есть числовое значение буквенного выражения.
Заметим, что и числовые и буквенные выражения можно называть еще как алгебраические выражения.
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5) 2 — x (x — 10) = x 2 + 2 • 5 • x + 25 — x 2 + 10x
Затем приведем подобные слагаемые:
x 2 + 2 • 5 • x + 25 — x 2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24
pазбирался: Даниил Романович | обсудить разбор | оценить
На координатной прямо отмечены числа a и b:
Какое из приведенных утверждений для этих чисел неверно:
Для удобства решения необходимо оценить данные нам числа. Из координатной прямой видно, что a > 0, так как расположено справа от ноля, а b 0
Значит, утверждение неверно.
pазбирался: Даниил Романович | обсудить разбор | оценить
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Числовые, буквенные выражения и выражения с переменными: определения, примеры.
Запись условий задач с помощью принятых в математике обозначений приводит к появлению так называемых математических выражений, которые называют просто выражениями. В этой статье мы подробно поговорим про числовые, буквенные выражения и выражения с переменными: дадим определения и приведем примеры выражений каждого вида.
Навигация по странице.
Числовые выражения – что это?
Можно сделать вывод, что на этом этапе изучения математики числовыми выражениями называют имеющие математический смысл записи, составленные из чисел, скобок и знаков сложения и вычитания.
А в старших классах разнообразие записей числовых выражений разрастается как снежный ком, катящийся с горы. В них появляются обыкновенные и десятичные дроби, смешанные числа и отрицательные числа, степени, корни, логарифмы, синусы, косинусы и так далее.
Обобщим всю информацию в определение числового выражения:
Разъясним все составные части озвученного определения.
В числовых выражениях могут участвовать абсолютно любые числа: от натуральных до действительных, и даже комплексных. То есть, в числовых выражениях можно встретить
Что касается скобок, то имеют место как числовые выражения, в которых есть скобки, так и выражения без них. Если в числовом выражении есть скобки, то они в основном
В качестве специальных математических символов и обозначений, которые можно встретить в числовых выражениях, приведем знак модуля. Для примера покажем числовое выражение с модулем 
Что такое буквенные выражения?
Итак, если допустить в числовом выражении присутствие букв, которыми обозначены некоторые числа, то получится так называемое буквенное выражение. Дадим соответствующее определение.
Выражение, содержащее буквы, которыми обозначены некоторые числа, называется буквенным выражением.
Из данного определения понятно, что принципиально буквенное выражение отличается от числового выражения тем, что может содержать буквы. Обычно в буквенных выражениях используются маленькие буквы латинского алфавита ( a, b, c, … ), а при обозначении углов – маленькие буквы греческого алфавита ( α, β, γ, … ).
Итак, буквенные выражения могут быть составлены из чисел, букв и содержать все математические символы, которые могут встречаться в числовых выражениях, такие как скобки, знаки корней, логарифмы, тригонометрические и другие функции и т.п. Отдельно подчеркнем, что буквенное выражение содержит по крайней мере одну букву. Но может содержать и несколько одинаковых или различных букв.
Выражения с переменными
Если в буквенном выражении буква обозначает величину, которая принимает не какое-то одно конкретное значение, а может принимать различные значения, то эту букву называют переменной и выражение называют выражением с переменной.
Выражение с переменными – это буквенное выражение, в котором буквы (все или некоторые) обозначают величины, принимающие различные значения.
Вообще, переход от понятия буквенного выражения к выражению с переменными происходит в 7 классе, когда начинают изучать алгебру. До этого момента буквенные выражения моделировали какие-то конкретные задачи. В алгебре же начинают смотреть на выражение более общо, без привязки к конкретной задаче, с пониманием того, что данное выражение подходит под огромное число задач.
В заключение этого пункта обратим внимание еще на один момент: по внешнему виду буквенного выражения невозможно узнать, являются ли входящие в него буквы переменными или нет. Поэтому ничто нам не мешает считать эти буквы переменными. При этом разница между терминами «буквенное выражение» и «выражение с переменными» исчезает.
Числовые и буквенные выражения. Формулы
Урок 9. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Числовые и буквенные выражения. Формулы»
Представим себе такую историю.
– Паша, я вчера смотрел чемпионат мира «Формулы-1»! – рассказывал Саша. – Это такое зрелище! Ты только представь себе: болиды «Формулы-1» могут развить скорость аж до четырёхсот километров в час. Вот бы мне так погонять!
– Саша, ты что? – перебил Паша. – Это очень опасная скорость. И чтобы научиться так ездить, нужно многие годы тренироваться. А ты знаешь, что в математике тоже есть формулы?
– Формулы? – удивился Саша. – Ты хочешь сказать, что цифры устраивают гонки?
– Нет, Саша! Ты такой смешной! – засмеялся Паша. – Математические формулы совсем другие. Но лучше всех нам о них расскажет только Электроша.
– Ребята, прежде чем я вам расскажу о формулах, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– Ну а теперь поговорим о формулах, – предложил Электроша, – но прежде вам нужно разобраться в понятиях «числовое выражение» и «буквенное выражение».
Чтобы в них разобраться, ответьте мне на вопрос: как найти периметр прямоугольника, стороны которого равны, например, 4 и 8 см?
– Ну это же все знают, – начал Саша. – Периметр прямоугольника – это сумма длин всех его сторон. Тогда периметр нашего прямоугольника равен 4 + 8 + 4 + 8.
– Саша, – перебил Паша, – но в прямоугольнике же две пары равных сторон. Значит, вычислить периметр нашего прямоугольника можно было следующим образом: 2 умножить на 4 плюс 3 умножить на 8.
– Не спорьте, ребята, – сказал Электроша. – Вы оба правы! Периметр прямоугольника можно вычислить и первым, и вторым способом. Записи, которые вы составили, называют числовыми выражениями.
Запомните! Числовое выражение – это выражение, составленное из чисел, знаков арифметических действий и скобок.
– Электроша, а вот такая запись тоже будет числовым выражением? – решил спросить Саша.
– Нет, Саша, – ответил Электроша. – Важно понимать, что не всякая запись, составленная из чисел, знаков арифметических действий и скобок, будет являться числовым выражением. Запись, которую показал нам Саша, представляет собой бессмысленный набор символов.
В записи выражений никогда не применяются знаки равенств и неравенств.
– А теперь, может, вы мне скажете, чему же равен периметр нашего прямоугольника? – спросил Электроша.
– Периметр прямоугольника равен 24 см, – ответили мальчишки.
– Правильно! – подтвердил Электроша. – Число, которое получают в результате выполнения всех действий в числовом выражении, называют значением этого выражения.
Выражение не имеет значения, если какое-либо из действий в нём нельзя выполнить.
– А теперь скажите, чему равен периметр прямоугольника, стороны которого равны, например, 4 см и а см?
– Периметр этого прямоугольника будет равен 2 умножить на 4 плюс 5 умножить на а, – ответил Паша.
– Молодец! – похвалил Пашу Электроша. – Запись «2 умножить на 4 плюс 2 умножить на а» называют буквенным выражением.
Запомните! Буквенное выражение – это выражение, которое составлено из чисел, букв, знаков арифметических действий и скобок.
Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют ещё переменными. Если в буквенное выражение вместо буквы подставить число и выполнить все действия, то получим значение буквенного выражения.
Давайте вместо а в нашем буквенном выражении подставим число 10. Получим числовое выражение 2 умножить на 4 плюс 2 умножить на 10 равно 28. В этом случае число 28 является значением нашего буквенного выражения при а = 10.
– А буквенные выражения всегда имеют значения? – спросили мальчишки.
– Хороший вопрос! – ответил Электроша. – Буквенное выражение может не иметь значения в случае, если при подстановке значений букв в буквенное выражение получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называют некорректным для натуральных чисел. Говорят также, что значение такого выражения не определено для натуральных чисел, а само выражение не имеет смысла.
Например, найдём значение буквенного выражения а – b при а = 20, b = 25.
– Электроша, но 20 меньше 25, – заметили ребята, – а в вычитании натуральных чисел уменьшаемое всегда должно быть больше вычитаемого.
– Правильно вы заметили, – сказал Электроша. – В таком случае говорят, что выражение не имеет смысла при указанных а и b.
Как правило, в буквенных выражениях числовой множитель (коэффициент) пишут перед буквой, а знак умножения ставят только между числами. Например, вместо 2 умножить на а пишут просто 2а. Или вместо выражения 2 умножить на сумму чисел а и b пишут 2(a + b).
– А теперь скажите, чему равен периметр прямоугольника, стороны которого равны а см и b см?
– Периметр такого прямоугольника можно вычислить выражением 2а + 2b, – сказал Паша.
– Молодец! – похвалил Электроша. – Если мы подставим в это выражение вместо букв а и b соответственно числа 4 и 8, то получим числовое выражение 2 умножить на 4 плюс 2 умножить на 8. Это числовое выражение мы уже записывали для нахождения периметра первого прямоугольника. Если вместо букв а и b мы подставим, например, числа 4 и 10, то получим числовое выражение 1 умножить на 4 плюс 2 умножить на 10. Такое числовое выражение мы тоже уже записывали для вычисления периметра второго прямоугольника.
– Так что, Электроша, вместо чисел а и b можно подставлять разные числа? – спросили ребята.
– Да! – ответил Электроша. – Из одного буквенного выражения можно получить бесконечно много различных числовых выражений.
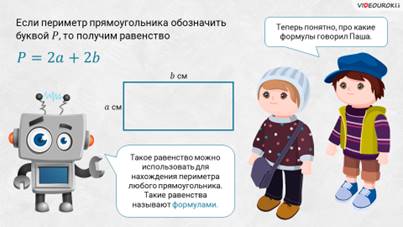
Если периметр прямоугольника обозначить буквой P, то получим равенство P = 2а + 2b. Такое равенство можно использовать для нахождения периметра любого прямоугольника. Такие равенства называют формулами.
– А! – воскликнул Саша. – Теперь понятно, про какие формулы говорил Паша.
Запомните! Правило, записанное в виде равенства двух буквенных выражений, называется формулой.
– Вы уже знакомы с некоторыми формулами, – продолжил Электроша. – Может, назовёте их?
– Если сторона квадрата равна а, то его периметр можно вычислить по формуле P = 4а, – начал Саша.
– А я ещё знаю формулу пути: S = vt, – продолжил Паша. – Здесь S – это пройденный путь, v – скорость движения, а t – время, за которое пройден путь S.
– Какие вы молодцы! – похвалил ребят Электроша. – А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
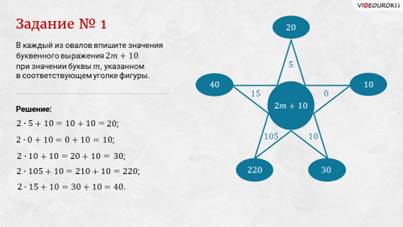
Задание первое: в каждый из овалов впишите значения буквенного выражения два эм плюс десять при значении буквы эм, указанном в соответствующем уголке фигуры.
Решение: начнём с первого уголка фигуры. Здесь m = 5. Подставим число 5 вместо m в буквенное выражение 2m + 10. Посчитаем. Получим 20. В следующем уголке записано число 0. Подставим его вместо буквы m в выражение. Получим 2 умножить на 0 плюс 10. Посчитаем и получим 10. Следующее число 10. Подставим его в выражение вместо буквы m. Получим 30. В следующем уголке записано число 105. Подставим его в выражение. Посчитаем и получим 220. И последнее число 15. Подставим его в выражение и посчитаем. Получим 40.
Следующее задание: заполните таблицу.
Решение: в первой строчке нам известно, что пешеход прошёл 8 минут со скоростью 70 м/мин. Воспользуемся формулой пути. Подставим в неё известные нам скорость и время. Посчитаем и получим, что пешеход прошёл 560 метров. В следующей строчке нам известно, что велосипедист за 2 часа проехал 24 км. Нужно узнать, с какой скоростью он ехал. Из формулы пути выразим скорость. Подставим наши данные в формулу. Посчитаем и получим, что скорость велосипедиста 12 км/ч. И в последней строчке нам известно, что автомобиль ехал со скоростью шестьдесят километров в час и проехал 240 км. Нужно узнать, сколько времени ехал автомобиль. Выразим из формулы пути время. Подставим в формулу известные значения. Посчитаем и получим, что автомобиль ехал 4 часа.
– Ребята, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.
Итак, Наташа купила в подарок своей маме шоколадное сердечко. Сколько весит эта шоколадка, если каждый квадратик весит 10 г?
Решение: сердечко состоит из 32 целых квадратиков и из 16 половинок квадратиков. Так как целый квадратик весит 10 г, то половинка квадратика весит 5 г. А тогда вес всего шоколадного сердечка можно найти так: 32 умножить на 10 + 16 умножить на 5. Посчитаем и получим, что сердечко весит 400 г.