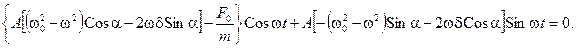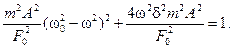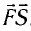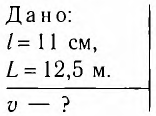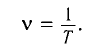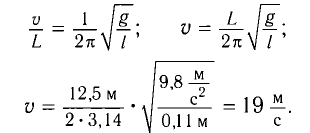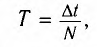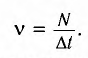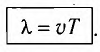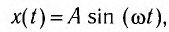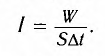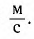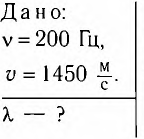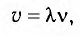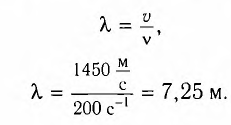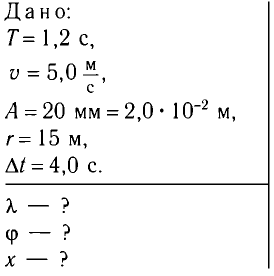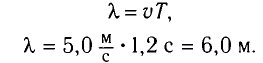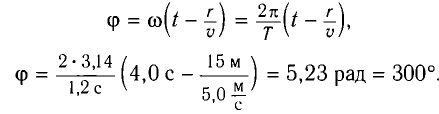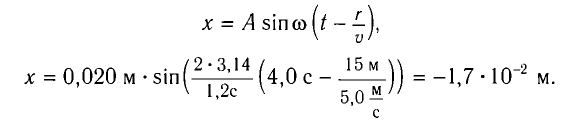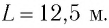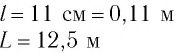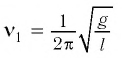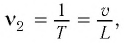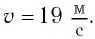Чем определяются частота и амплитуда вынужденных колебаний

Вынужденные колебания. Резонанс. Амплитуда и фаза вынужденных колебаний

Рассмотрим колебания, которые поддерживаются в системе внешней гармонической силой F = F₀Coswt. Такие колебания называются вынужденными.

Обратимся вновь к пружинному маятнику. Вспомним уравнения движения этого осциллятора:

— уравнение собственных незатухающих колебаний. В системе действует одна упругая сила F_упр = –kx;

— собственные затухающие колебания. В системе появилась сила вязкого сопротивления, пропорциональная скорости .

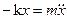
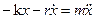
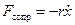
В случае вынужденных колебаний кроме двух названных сил — упругой и силы сопротивления, на систему действует ещё одна сила: F = F₀Coswt.

— дифференциальное уравнение вынужденных колебаний пружинного маятника. Это уравнение движения принято записывать так:

.

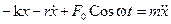
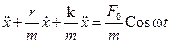
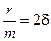
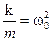
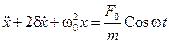
Введя знакомые обозначения и , представим уравнение движения осциллятора окончательно в таком виде:

. (13.14)

Опыт показывает, что под действием гармонического возмущающего усилия F = F₀Coswt осциллятор совершает гармонические колебания с частотой вынуждающей силы w:

Если частота w известна, то задача сводится к определению амплитуды вынужденных колебаний А и начальной фазы a.

Продифференцировав функцию (13.15), подставим ее в уравнение (13.14):

.

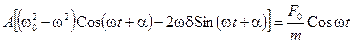
Теперь воспользуемся известными тригонометрическими формулами для косинуса и синуса суммы двух углов:

Это уравнение представляет собой сумму двух гармонических слагаемых

Последнее равенство возможно в единственном случае, если постоянные во времени a и b равны нулю: а = 0, b = 0. Это означает, что справедливы следующие уравнения:

, (13.16)

. (13.17)

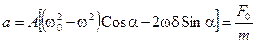
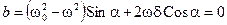
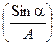
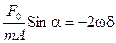
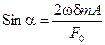
Эти два уравнения содержат только две неизвестные величины: амплитуду А и фазу a вынужденного колебания. Для отыскания амплитуды А можно домножить уравнение (13.16) на , а уравнение (13.17) — на Cosa. Вычтя теперь из первого уравнения второе, получим Sina:

,

. (13.18)

Воспользовавшись этим результатом в уравнении (13.17), найдем Cosa:

. (13.19)

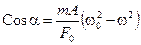
Возведем уравнения (13.18) и (13.19) в квадрат и сложим:

Последнее уравнение решим относительно искомой амплитуды колебаний А:

. (13.20)

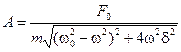
Фазовый сдвиг смещения x относительно возмущающего усилия F найдём непосредственно из уравнения (13.17):

. (13.21)

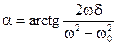
Обратимся к анализу полученных результатов.

1) Амплитуда вынужденных колебаний прямо пропорциональна амплитуде возмущающего усилия F₀.

2) Если w = 0 — случай приложения статической нагрузки F₀, смещение груза будет определяться жёсткостью пружины k:

.

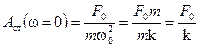
3) При высоких частотах внешнего усилия (w→¥), амплитуда колебаний А→0.

4) Для отыскания частоты w_рез, при которой амплитуда достигает наибольшего значения А_рез, нужно найти минимум выражения, стоящего под корнем в знаменателе уравнения (13.20). Продифференцировав это выражение по w, и приравняв результат нулю, получим условие, определяющее w_рез:

.

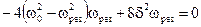
Отсюда следует, что резонансная частота w_рез меньше частоты собственных незатухающих колебаний w₀:

. (13.22)

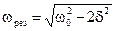
Используя это значение в (13.20), рассчитаем резонансную амплитуду:

. (13.23)

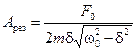
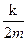
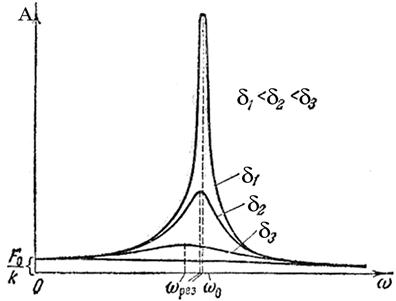
5) Если вязкое сопротивление отсутствует, коэффициент затухания d = = 0 и резонансная амплитуда устремляется в бесконечность. При этом условии резонансная частота, как следует из (13.22), равна частоте собственных незатухающих колебаний осциллятора w_рез = w₀.

6) С увеличением коэффициента затухания d, резонансная частота и амплитуда колебаний уменьшаются.

Все эти закономерности графически представлены на рис. 13.4.

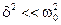
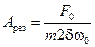
7) При слабом затухании, когда , резонансная амплитуда равна

.

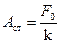
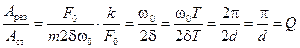
Разделим это выражение на — смещение под действием постоянной силы:

.

Таким образом, добротность осциллятора численно равна отношению резонансной амплитуды к смещению под действием постоянной силы.

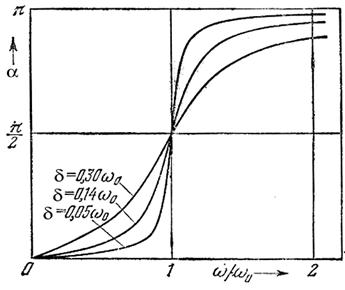
8) На рис. 13.5 представлена зависимость фазового сдвига вынужденных колебаний и вынуждающей силы — график функции (13.21). С увеличением частоты вынуждающего усилия a растет, меняясь от 0 до p. В резонансе фазовый сдвиг равен . Эта зависимость a = a(w) меняется с изменением коэффициента затухания.

Лекция 14 «Элементы специальной теории относительности»

1. Постулаты специальной теории относительности. Преобразования Лоренца.

2. Динамика релятивистского движения.

3. Закон эквивалентности массы и энергии.

В классической механике Ньютона мы изучали законы движения макротел со скоростями, далекими от скорости света (с = 3 × 10 8 м/с). Такие движения называются нерелятивистскими (классическими), в отличие от релятивистских движений, скорость которых соизмерима со скоростью света. Теоретической основой релятивистской механики является специальная (частная) теория относительности (СТО). Предваряя рассмотрение основных положений этой теории, отметим два важных момента:

1) Релятивистская механика включает в себя и классическую механику как предельный случай движения с малыми скоростями.

2) Все положения СТО имеют сегодня надежное экспериментальное подтверждение.

Источник

11 класс

§ 28. Вынужденные колебания. Резонанс

Вынужденные колебания.

Наиболее простой способ возбуждения незатухающих колебаний состоит в том, что на колебательную систему действует внешняя периодически изменяющаяся сила. Колебания под действием такой силы называют вынужденными.

Работа вынужденной силы над системой обеспечивает приток энергии к системе извне, который и не даёт колебаниям затухать, несмотря на действие сил трения.

Исследования физических явлений опытным путём

Рассмотрим вместо маятника груз, подвешенный на пружине. Но теперь верхний конец пружины будет прикреплён к «колену» изогнутой оси (рис. 5.16).

Если вращать ось с помощью рукоятки, то на груз, прикреплённый к пружине, начнёт действовать периодически изменяющаяся внешняя сила. Ещё лучше вращать ось с помощью электродвигателя. Это обеспечит большую стабильность частоты внешней силы.

Груз начнёт раскачиваться, амплитуда его колебаний будет увеличиваться. Спустя некоторое время колебания приобретут установившийся характер: их амплитуда со временем перестанет изменяться. При этом можно обнаружить, что частота колебаний груза будет в точности равна частоте колебаний точки подвеса пружины, т. е. частоте изменения внешней силы.

Установившиеся вынужденные колебания происходят с частотой ω и амплитудой х_m по гармоническому закону:

где φ_c — разность (сдвиг) фаз между колебаниями координаты и внешней силы.

Внешне вынужденные установившиеся колебания выглядят так же, как и свободные колебания в системе без трения. Но если при свободных колебаниях амплитуда х_m и начальная фаза φ₀ определяются начальными условиями, то при вынужденных колебаниях х_m и φ_c определяются параметрами самой системы и внешней силой.

Выясним, от чего и как зависят амплитуда х_m вынужденных колебаний и сдвиг фаз φ_c. Для этого запишем и исследуем уравнение движения для вынужденных колебаний.

1 При малых скоростях движения тела силу сопротивления можно считать пропорциональной скорости.

Тогда уравнение движения запишется следующим образом:

Перенеся в левую часть уравнения все силы, кроме внешней, получим

Разделим правую и левую части данного уравнения на т и обозначим собственную частоту системы через :

Если частота ω внешней периодической силы много меньше частоты собственных колебаний системы (ω ≪ ω₀), происходит почти то же самое, что и при действии на пружину постоянной силы. Согласно закону Гука, смещение увеличивается пропорционально внешней силе, и в любой момент времени внешняя сила почти точно уравновешивается силой упругости пружины. C энергетической точки зрения условия для перекачки энергии в колебательную систему от внешних тел, действующих на систему с периодической силой, в данном случае неблагоприятны.

Рассмотрим случай, при котором ω » ω₀. Амплитуда колебаний будет мала. Внешняя сила столь быстро меняет направление, что груз на пружине, обладающий инертностью, не успевает заметно сдвинуться относительно положения равновесия. Половину периода внешняя сила совершает положительную работу, а другую половину — отрицательную. Половину периода сила и перемещение направлены в одну сторону, а другую его половину — в противоположные стороны. Энергия опять почти не поступает в систему.

Резонанс.

Самый интересный случай вынужденных колебаний наблюдается при совпадении частоты колебаний внешней периодически изменяющейся силы с собственной частотой колебаний системы (ω ≈ ω₀).

2 Если собственная частота колебательной системы и частота внешней силы существенно различаются, то внешняя сила совершает положительную работу лишь в течение части периода, а в другой его части — отрицательную работу.

Тем самым создаются оптимальные условия для перекачки энергии от внешних тел к колебательной системе: положительная работа внешней силы равна по модулю отрицательной работе силы сопротивления. Из-за этого механическая энергия системы за счёт работы силы сопротивления переходит во внутреннюю энергию (пружина с грузом и окружающий воздух нагреваются).

Амплитуда колебаний при ω ≈ ω₀ равна

При k₁ → 0 x_m → ∞, т. е. очевидно, что при ω ≈ ω₀ амплитуда максимальна.

Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний называют резонансом.

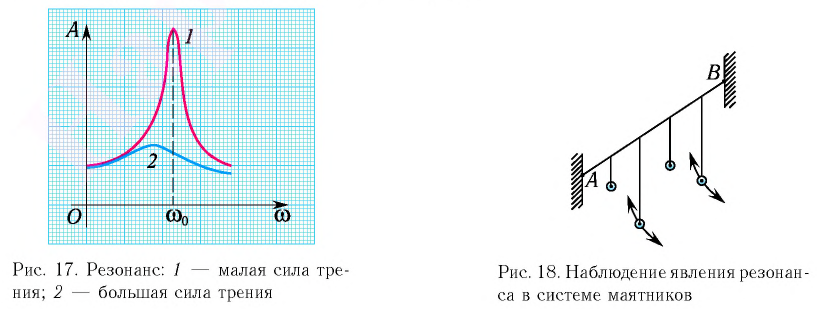
Явление резонанса можно наблюдать с помощью установки, изображённой на рисунке 5.16. Плавно увеличивая частоту внешней силы, мы заметим, что амплитуда колебаний растёт. Она достигает максимума, когда внешняя сила действует в такт со свободными колебаниями (ω ≈ ω₀). При дальнейшем увеличении частоты амплитуда установившихся колебаний опять уменьшается (рис. 5.17).

Существенное влияние на резонанс оказывает сопротивление в системе. Если коэффициент сопротивления k₁ имеет достаточно большое значение, то, согласно уравнению (2), резонансная амплитуда колебаний невелика. Чем меньше сила сопротивления, тем больше амплитуда установившихся вынужденных колебаний.

Изменение амплитуды колебаний в зависимости от частоты при различных коэффициентах сопротивления (k₁ 1 с двумя выступами по краям. C помощью анкера маятник управляет вращением храпового колеса и связанной с ним стрелки часов. При этом энергия от гири порциями поступает к маятнику. В изображённом на рисунке положении зубец давит на скос выступа b анкера и толкает маятник влево.

1 Немецкое слово «анкер» означает «якорь».

После прохождения маятником положения равновесия выступ b соскальзывает с зубца, но почти сразу же анкер внешним скосом выступа а упирается в другой зубец храпового колеса, и маятник испытывает толчок в другую сторону. В результате дважды за период маятник получает энергию, сам открывая и закрывая доступ энергии от источника. Незатухающие колебания маятника происходят с частотой, почти точно равной частоте его свободных колебаний, если трение в системе мало. Именно поэтому часы обладают регулярным ходом.

Системы, подобные часам, в которых генерируются незатухающие колебания за счёт поступления энергии от источника, называют автоколебательными системами. Незатухающие колебания, которые могут существовать в системе без воздействия на неё внешних периодических сил, называются автоколебаниями.

Автоколебания отличаются от свободных колебаний тем, что, во-первых, они не затухают с течением времени и, во-вторых, их амплитуда не зависит от начального кратковременного воздействия («толчка»), которое возбуждает колебания. Частота и амплитуда автоколебаний определяются свойствами самой системы.

К автоколебательным системам относят также электрический звонок с прерывателем, органную трубу, свисток и многое другое. Наше сердце и лёгкие тоже можно рассматривать как автоколебательные системы.

Вопросы:

1. Какие колебания называют вынужденными?

2. Как записывается уравнение движения для вынужденных колебаний?

3. В чём состоит явление резонанса?

4. Почему при резонансе создаются оптимальные условия для перекачки энергии от внешних тел к системе?

5. Какое влияние оказывает сопротивление в системе на резонанс?

6. Какие колебания называют автоколебаниями? Чем они отличаются от свободных колебаний?

Вопросы для обсуждения:

1. Если длину математического маятника уменьшать, когда он проходит положение равновесия, и увеличивать в те моменты, когда его отклонение максимально, то амплитуда колебаний маятника начинает возрастать. Как это можно объяснить?

2. Почему при некоторой скорости движения оконные стёкла в пассажирском автобусе начинают дребезжать?

3. Для того чтобы отвести качели с сидящим на них человеком на больший угол, необходимо приложить значительную силу. Почему же раскачать качели до такого же угла отклонения можно с помощью значительно меньшего усилия?

Упражнения:

1. Груз массой 200 г на пружине с жёсткостью 100 Н/м совершает колебания, график которых представлен на рисунке 5.20.

Почему при этом уменьшается амплитуда колебаний?

Чему равна механическая энергия колебательной системы в начальный момент времени?

Через какое время эта энергия уменьшится в 4 раза?

2. На рисунке 5.21 приведена резонансная кривая для балки, на которой укреплён электродвигатель.

При какой частоте вращения ротора будут наблюдаться сильные колебания балки?

3. При какой скорости поезда возникает резонанс, если длина железнодорожного рельса между стыками равна 25 м, а период собственных колебаний вагона составляет 1,25 с?

Источник

I. Механика

Тестирование онлайн

Колебательное движение

Колебательная система

Это система взаимодействующих тел (минимум два тела), которые способны совершать колебания. Простейшими колебательными системами являются маятники.

Характеристика колебаний

Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.

Циклическая частота характеризует скорость изменения фазы колебаний.

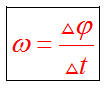
Начальное состояние колебательной системы характеризует начальная фаза

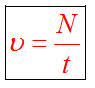
Частота, циклическая частота и период колебаний соотносятся как

Виды колебаний

Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными. Встречаются также автоколебания (вынуждаются автоматически).

Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические, затухающие, нарастающие (а также пилообразные, прямоугольные, сложные).

При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.

Вынужденные колебания. Резонанс

Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.

Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.

Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.

Примеры резонанса

Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать

Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.

Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.

Источник

Содержание:

Свободные и вынужденные колебания:

Работа силы вычисляется по формуле А =

Как Вам уже известно, механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды его колебаний. Колебания, происходящие с постоянной во времени амплитудой, называются незатухающими колебаниями.

Незатухающие колебания, вызванные кратковременным внешним воздействием, называются свободными или собственными. Они происходят под действием внутренних сил, возникающих в самой системе. Свободные колебания — это колебания, происходящие в отсутствие внешних воздействий на систему, со строго определенной частотой, называемой частотой собственных колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения.

В любой реальной системе всегда присутствуют силы трения (сопротивления), поэтому механическая энергия системы с течением времени уменьшается, переходя во внутреннюю энергию. Вместе с тем убыль механической энергии означает и уменьшение амплитуды колебаний.

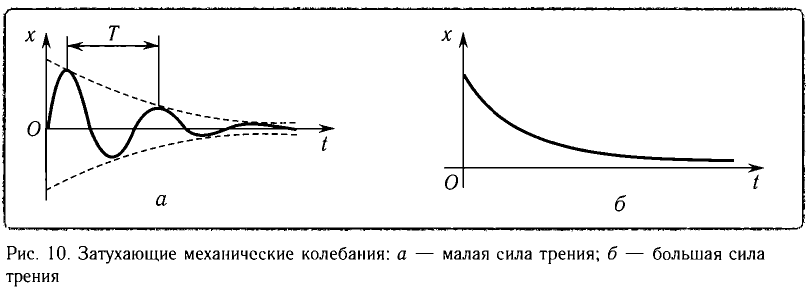
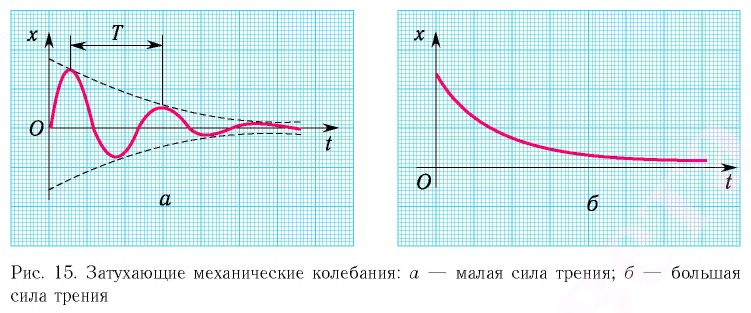
Колебания, амплитуда которых уменьшается с течением времени вследствие потери энергии колебательной системой, называются затухающими колебаниями (рис. 10, а, б).

Уменьшение механической энергии системы (превращение ее во внутреннюю энергию) происходит вследствие трения и сопротивления окружающей среды. Такие системы называют диссипативными (от латинского слова dissipation — рассеяние).

При малых потерях энергии колебания можно считать периодическими и пользоваться такими понятиями, как период и частота колебаний. Так, например, период — промежуток времени между двумя последовательными максимумами колеблющейся физической величины (см. рис. 10, а).

Любые собственные колебания в реальной системе рано или поздно затухают. Чтобы колебания не затухали, необходимо воздействие внешней силы. Однако не всякая внешняя сила заставляет систему двигаться периодически. Например, невозможно раскачать качели, если действовать на них с постоянной по модулю и направлению силой. Внешняя сила тоже должна быть периодической.

Колебания тел под действием внешней периодической силы называются вынужденными, а сила — вынуждающей. В случае гармонической силы 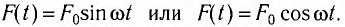. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.

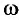
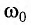
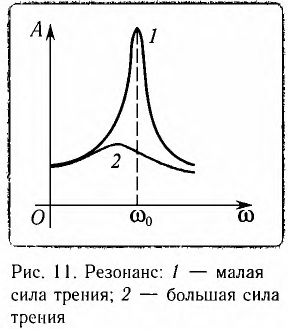
Амплитуда колебаний и энергия, передаваемая системе за период вынужденных колебаний, зависят от того, насколько различаются частота вынуждающей силы и частота собственных колебаний , а также от величины трения в системе.

При вынужденных колебаниях возможно явление, называемое резонансом (от латинского слова resono — откликаюсь, звучу в ответ).

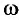
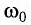
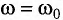
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при действии на колебательную систему внешней силы с частотой , совпадающей с собственной частотой системы (() (рис. 11).

При резонансе создаются оптимальные условия для передачи системе энергии от внешнего источника, так как в течение всего периода работа внешней силы над системой положительна. Вспомните процесс раскачивания на качелях — если качели толкать с большой частотой или с малой, то их практически невозможно раскачать. Если же подобрать частоту толчков, близкую к частоте собственных колебаний качелей, то раскачивание будет эффективным.

Пример №1

Определите модуль скорости v движения поезда, при которой маятник длиной l=11 см, подвешенный в вагоне, особенно сильно раскачивается. Длина рельса L = 12,5 м.

Решение

Маятник начинает сильно раскачиваться, когда частота его собственных колебаний совпадает с частотой вынуждающей

Частотой вынуждающей силы является частота ударов колес вагона о стыки рельс. Промежуток времени между двумя последовательными ударами (период)

(1)

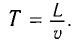
Поскольку частота — величина, обратная периоду, то можно записать частоту вынуждающей силы

Частота собственных колебаний математического маятника

(2)

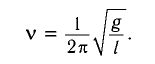
Приравняв формулы (I) и (2), получим

Ответ: о = .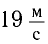

Распространение колебаний в упругой среде. Продольные и поперечные волны

Опыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. Так от камня, брошенного в спокойную воду озера, кругами расходятся волны, которые со временем достигают берега. Колебания сердца, расположенного внутри грудной клетки, можно ощутить на запястье, что используется для определения пульса.

Перечисленные примеры связаны с явлением распространения механических колебаний в среде.

Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.

Механические волны не могут распространяться в вакууме.

Источником механических волн является колеблющееся тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в ней с определенной скоростью, зависящей от плотности и упругих свойств среды.

Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц относительно положения равновесия за большой промежуток времени равно нулю.

Механизм образования волны можно представить следующим образом. Источник волны — колеблющееся тело — воздействует на частицы упругой среды, соприкасающиеся с ними, и заставляет их совершать вынужденные колебания. Среда вблизи источника деформируется, и в ней возникают силы упругости, препятствующие деформации. Если частицы среды сближаются, то возникают силы отталкивания, а если они удаляются друг от друга, то — силы притяжения. Постепенно эти силы будут действовать на все более удаленные от источника частицы среды, приводя их в колебательное движение, которое будет распространяться в виде волны.

Рассмотрим основные характеристики волны.

Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени.

Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны.

Основные характеристики волны:

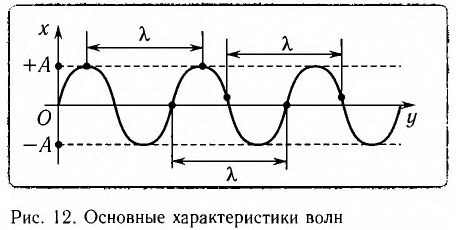
Амплитуда (А) — модуль максимального смещения точек среды из положений равновесия при колебаниях (рис. 12).

Период (Т) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны):

где 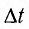— промежуток времени, в течение которого совершаются N колебаний.

Частота (v) — число полных колебаний, совершаемых в данной точке в единицу времени:

Частота волны определяется частотой колебаний источника.

Скорость (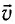) — скорость перемещения гребня волны (это не скорость частиц! ).

Длина волны (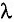) — наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника (см. рис. 12):

Рассмотрим колебания источника волны, происходящие с циклической частотой 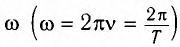и амплитудой А:

где x(t) — смещение источника от положения равновесия.

В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна у, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии г от источника, описывается уравнением

(1)

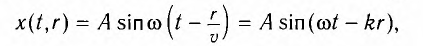
где k — волновое число 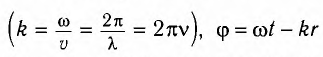— фаза волны.

Выражение (1) называется уравнением распространяющейся (бегущей) волны.

Бегущую волну можно наблюдать при следующем эксперименте: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна.

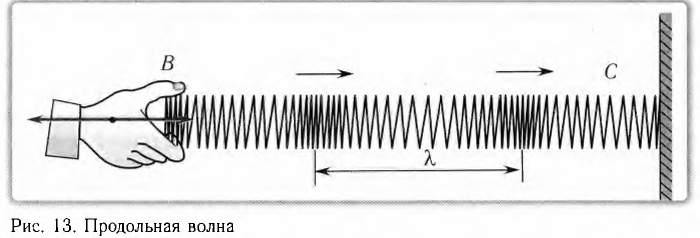
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Упругие волны в газах и жидкостях возникают только при сжатии или разрежении среды. Поэтому в таких средах возможно распространение только продольных волн.

Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 13). При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в газе и жидкости.

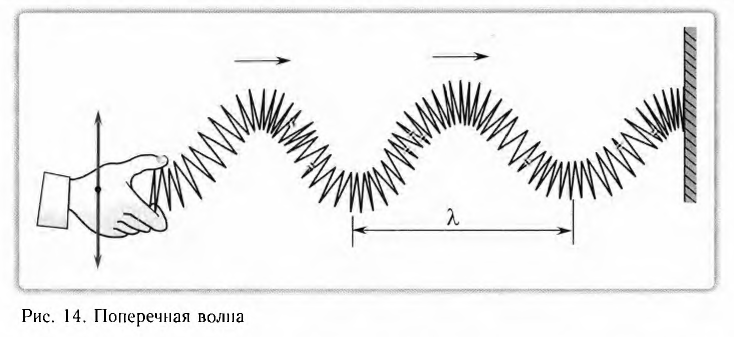
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. Используя длинную пружину, можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно продольной оси пружины (рис. 14). В твердых телах упругие волны могут возникать также и при смещении или сдвиге одних слоев среды относительно других. Поэтому в отличие от жидкостей и газов в твердых телах возможно распространение и поперечных волн.

Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.

Для характеристики энергии, переносимой волнами, используется понятие интенсивности волны (l), определяемое как энергия (W), переносимая волной в единицу времени (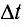= 1с) через поверхность площадью S= I м2, расположенную перпендикулярно к направлению распространения волны:

Другими словами, интенсивность представляет собой мощность, переносимую волнами через поверхность единичной площади, перпендикулярно к направлению распространения волны. Единицей интенсивности в СИ является
ватт на метр в квадрате ().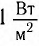

Волны могут распространяться не только в среде, но и вдоль границы раздела двух сред. Такие волны получили название поверхностных волн. Примером данного типа волн служат хорошо знакомые всем волны на поверхности воды.

Пример №2

Определите длину X волны, излучаемой источником колебаний с частотой v = 200 Гц, если модуль скорости распространения волны v = 1450

Решение

Модуль скорости распространения волны можно вычислить по формуле

где 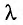— длина волны, v — частота колебаний. Откуда находим

Ответ: 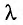= 7,25 м.

Пример №3

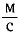
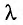
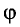
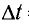
Поперечная волна распространяется вдоль упругого шнура со скоростью, модуль которой v = 5,0/ Период колебания точек шнура Т= 1,2 с, амплитуда колебаний A = 20 мм. Определите длину волны , фазу колебаний и смещение х точки, находящейся на расстоянии г= 15 м от источника колебаний, через промежуток времени = 4,0 с.

Решение

Длина волны находится из выражения

Волна пройдет расстояние г за время 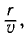следовательно, фаза колебаний определится по формуле

Подставив вычисленное значение фазы в уравнение колебаний, получим:

Определение свободных и вынужденных колебаний

Силы взаимодействия тел системы называют внутренними. Тела, не входящие в систему, называют внешними телами. Силы, которые действуют на тела системы со стороны внешних тел, называют внешними силами.

Как вам уже известно, механическая энергия гармонического осциллятора (например, груза на пружине) пропорциональна квадрату амплитуды его колебаний. Колебания, происходящие с постоянной во времени амплитудой, называются незатухающими колебаниями.

Колебания, которые совершает система около положения устойчивого равновесия под действием внутренних сил после того, как она была выведена из состояния равновесия и предоставлена самой себе, называются свободными (собственными) колебаниями.

Свободные колебания происходят со строго определенной частотой 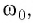называемой частотой свободных (собственных) колебаний системы. Эта частота зависит только от параметров системы. Примерами таких колебаний могут служить колебания математического и пружинного маятников, происходящие в отсутствие сил трения. Амплитуда свободных колебаний определяется начальными условиями, т. е. тем начальным отклонением или толчком, которым маятник или груз на пружине приведен в движение. Свободные колебания являются самым простым видом колебаний.

В любой реальной колебательной системе всегда присутствуют силы трения (сопротивления), поэтому механическая энергия системы с течением времени уменьшается, переходя во внутреннюю энергию. Вместе с тем убыль механической энергии означает и уменьшение амплитуды колебаний.

Колебания, амплитуда которых уменьшается с течением времени вследствие потери энергии колебательной системой, называются затухающими колебаниями (рис. 15). Уменьшение механической энергии системы (превращение ее во внутреннюю энергию) происходит вследствие трения и сопротивления окружающей среды.

Систему называют диссипативной (от лат. dissipation — рассеяние), если ее механическая энергия с течением времени уменьшается за счет превращения ее во внутреннюю энергию.

При малых потерях энергии колебания можно считать периодическими и пользоваться такими понятиями, как период и частота колебаний. Так, например, период — промежуток времени между двумя последовательными максимумами колеблющейся физической величины (см. рис. 15, а).

Колебания в любой реальной системе рано или поздно затухают. Чтобы колебания не затухали, необходимо воздействие внешней силы. Однако не всякая внешняя сила заставляет систему двигаться периодически. Например, невозможно раскачать качели, если действовать на них постоянной силой. Внешняя сила тоже должна быть периодической.

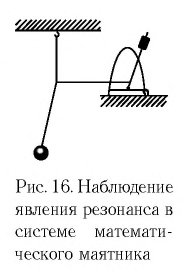
Проведем следующий эксперимент. Соединим математический маятник с метрономом (рис. 16). Изменяя частоту колебаний маятника метронома, добиваемся увеличения амплитуды колебаний математического маятника. Оказывается, что его амплитуда будет максимальной при совпадении собственной частота колебаний маятника и маятника метронома.

Колебания тел под действием внешней периодической силы называются вынужденными, а сила — вынуждающей. В случае гармонической силы: 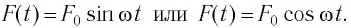Вначале действия внешней силы наблюдается достаточно сложное движение тела. Спустя некоторое время после начала действия внешней силы колебания приобретают стационарный характер и не зависят от начальных условий. Таким образом, при вынужденных колебаниях система полностью «забывает» свое начальное состояние. Частота установившихся вынужденных колебаний всегда равна частоте вынуждающей силы.

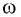
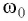
Амплитуда колебаний и энергия, передаваемая системе за период вынужденных колебаний, зависят от того, насколько различаются частота вынуждающей силы и частота собственных колебаний, а также от величины трения в системе.

При вынужденных колебаниях возможно явление, называемое резонансом (от лат. resono — откликаюсь, звучу в ответ).

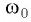
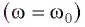
Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний при действии на колебательную систему внешней силы с частотой со, совпадающей с собственной частотой системы (рис. 17).

Подвесим на упругой нити 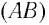четыре математических маятника с одинаковыми грузами, три из которых имеют различную длину, а длина четвертого равна длине второго (рис. 18). Сначала посмотрим, что будет с маятниками, если раскачать первый или третий маятник. Наблюдения показывают, что через некоторое время начнут качаться и остальные маятники. Но амплитуда их колебаний мала, и вскоре колебания затухают. А вот если раскачать второй маятник, то амплитуда колебаний четвертого будет непрерывно возрастать, пока не достигнет наибольшего значения.

Это происходит потому, что частота собственных колебаний четвертого маятника совпадает с частотой колебаний внешней силы (частотой колебаний второго маятника), так как их длины равны. А колебания первого и третьего маятников, как и в первом эксперименте, быстро затухают.

При резонансе создаются оптимальные условия для передачи системе энергии от внешнего источника, так как в течение всего периода работа внешней силы над системой положительна. Вспомните процесс раскачивания на качелях: если качели толкать очень быстро или очень медленно, их практически невозможно будет раскачать. Если же подбирать частоту толчков, близкую к частоте собственных колебаний качелей, то раскачивание будет эффективным.

Большинство сооружений и машин, обладая определенной упругостью, способны совершать свободные колебания. Поэтому при внешних периодических воздействиях в них вследствие явления резонанса могут возбуждаться колебания большой амплитуды, которые могут привести к разрушительным последствиям. Например, для исключения разрушения мостов вследствие явления резонанса при прохождении по ним войсковых частей приказывают идти вольным шагом (не в ногу). Поезда переезжают мосты либо очень медленно, либо с максимальной скоростью.

В 1750 г. цепной мост вблизи г. Анжер (Франция) был разрушен в результате резонанса, во время прохождения по нему отряда солдат, так как частота их шага совпала с частотой свободных колебаний моста.

В 1906 г. в г. Петербурге (Россия) обрушился Египетский мост, по которому проходил кавалерийский эскадрон.

7 ноября 1940 г. сильный порыв ветра вызвал резонансные колебания Такомского моста (США), что привело к его разрушению.

Пример №4

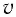
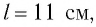
Определите модуль скорости движения поезда, при которой математический маятник, подвешенный в вагоне, особенно сильно раскачивается. Длина маятника длина рельса

Маятник начинает сильно раскачиваться, когда частота его собственных колебаний

совпадает с частотой вынуждающей силы

которая совпадает с частотой ударов колес вагона о стыки рельсов: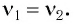
Отсюда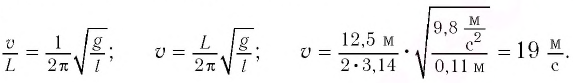

Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник