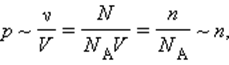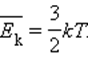Чем определяется температура с точки зрения мкт
Основное уравнение МКТ газов. Температура
Модель идеального газа считается самой простейшей относительно основных положений МКТ. Кинетическая модель идеального газа молекул говорит о том, что при взаимодействии между собой, шарики рассматриваются в качестве идеально упругих. Суммарный объем всех молекул достаточно мал по сравнению с объемом сосуда, в котором находится данный газ. Модель необходима для описания его поведения при различных давлениях и температурах.
Цель молекулярно-кинетической теории – установка связи между макроскопическими и макроскопическими параметрами.
После соударения молекул между собой и стенками сосуда происходит изменение направления движения и времени между интервалами столкновений. Модель идеального газа основывается на законах механики Ньютона, то тесть столкновения соответствуют закону упругого удара.
Распределением Максвелла называют распределение молекул газа по модулю скоростей.
Если растет температура, тогда максимум кривой будет смещен в сторону больших скоростей, то есть υ в и υ к в увеличатся.
Распределение Максвелла
Физика. Температура
Температура связана с понятием теплового равновесия. При контакте тела обмениваются энергией, которая передается и получает название количества теплоты.
Тепловым равновесием называют состояние системы тел, которые находятся в тепловом контакте с теплопередачей и с постоянными макроскопическими параметрами.
Температура измеряется с помощью термометра. Для его создания выбирается термометрическое вещество и величину, которая его характеризует. Разные конструкции подразумевают отличия в их свойствах.
Температура кипения газов при давлении
Температура кипения газов. Шкала Кельвина
Температурная шкала Кельвина считается абсолютной. Она наиболее приемлема для обозначения физических теорий.
Шкала Кельвина может быть не привязана двумя фиксированными точками, а именно: точка плавления льда и кипения воды с нормальным атмосферным давлением.
Нулевое давление называется абсолютным нулем температуры.
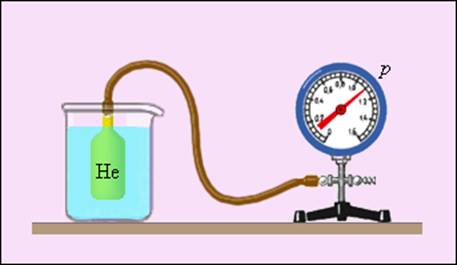
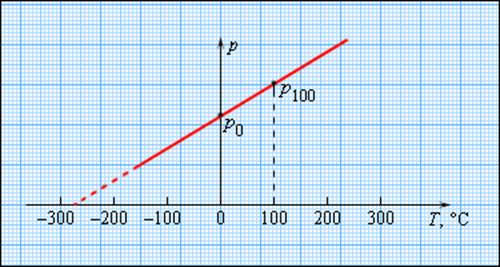
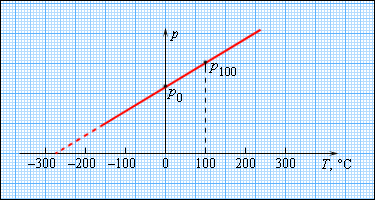
Шкала Кельвина имеет точку, в которой лед, вода и пар будут находиться в тепловом равновесии. Для калибровки других термометров применяют газовые, так как для практики они не подходят в виду своих больших размеров. Отсюда следует, что давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре, то есть p
υ V = N N A V = n N A
Средняя кинетическая энергия беспорядочного движения молекул газа прямо пропорциональна абсолютной температуре.
Температура
Хаотическое тепловое движение на плоскости частиц газа таких как атомы и молекулы
Содержание
Молекулярно-кинетическое определение
Температура с молекулярно-кинетической точки зрения — физическая величина, характеризующая интенсивность хаотического, теплового движения всей совокупности частиц системы и пропорциональная средней кинетической энергии поступательного движения одной частицы.
Связь между кинетической энергией, массой и скоростью выражается следующей формулой:
Ek = 1 /2m • v 2
Таким образом частицы одинаковой массы и имеющие одинаковую скорость имеют и одинаковую температуру.
Средняя кинетическая энергия частицы связана с термодинамической температурой постоянной Больцмана :
Eср = i/2kBT
где:
i — число степеней свободы kB = 1.380 6505(24) × 10 −23 Дж/K — постоянная Больцмана T — температура;
Термодинамическое определение
Температура — величина, обратная изменению энтропии (степени беспорядка) системы при добавлении в систему единичного количества теплоты: 1/T = ΔS/ΔQ.
История термодинамического подхода
Слово «температура» возникло в те времена, когда люди считали, что в более нагретых телах содержится большее количество особого вещества — теплорода, чем в менее нагретых. Поэтому температура воспринималась как крепость смеси вещества тела и теплорода. По этой причине единицы измерения крепости спиртных напитков и температуры называются одинаково — градусами.
В равновесном состоянии температура имеет одинаковое значение для всех макроскопических частей системы. Если в системе два тела имеют одинаковую температуру, то между ними не происходит передачи кинетической энергии частиц ( тепла ). Если же существует разница температур, то тепло переходит от тела с более высокой температурой к телу с более низкой, потому что суммарная энтропия при этом возрастает.
Температура связана также с субъективными ощущениями «тепла» и «холода», связанными с тем, отдает ли живая ткань тепло или получает его.
Некоторые квантовомеханические системы могут находится в состоянии, при котором энтропия не возрастает, а убывает при добавлении энергии, что формально соответствует отрицательной абсолютной температуре. Однако такие состояния находятся не «ниже абсолютного нуля», а «выше бесконечности», поскольку при контакте такой системы с телом, обладающим положительной температурой, энергия передается от системы к телу, а не наоборот (подробнее см. Квантовая термодинамика ).
Свойства температуры изучает раздел физики — термодинамика. Температура также играет важную роль во многих областях науки, включая другие разделы физики, а также химию и биологию.
Измерение температуры
Для измерения температуры выбирается некоторый термодинамический параметр термометрического вещества. Изменение этого параметра однозначно связывается с изменением температуры. На практике для измерения температуры используют
Единицы и шкала измерения температуры
Из того, что температура — это кинетическая энергия молекул, ясно, что наиболее естественно измерять её в энергетических единицах (т.е. в системе СИ в джоулях ). Однако измерение температуры началось задолго до создания молекулярно-кинетической теории, поэтому практические шкалы измеряют температуру в условных единицах — градусах.
Шкала температур Кельвина
Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К).
Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию.
Абсолютный ноль определён как 0 K, что приблизительно равно −273.15 °C.
Температуре замерзания воды при стандартном атмосферном давлении соответствуют 273,15 K. Число градусов Цельсия и кельвинов между точками замерзания и кипения воды одинаково и равно 100. Поэтому градусы Цельсия переводятся в кельвины по формуле K = °C + 273,15.
Шкала Цельсия
Шкала Фаренгейта
В Англии и, в особенности, в США используется шкала Фаренгейта. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а градус Фаренгейта равен 5/9 градуса Цельсия.
Энергия теплового движения при абсолютном нуле
Когда материя охлаждается, многие формы тепловой энергии и связанные с ней эффекты одновременно уменьшаются по величине. Вещество переходит от менее упорядоченного состояния к более упорядоченному. Газ превращается в жидкость и затем кристаллизуется в твёрдое тело (гелий и при абсолютном нуле остается в жидком состоянии при атмосферном давлении). Движение атомов и молекул замедляется, их кинетическая энергия уменьшается. Сопротивление большинства металлов падает из-за уменьшения рассеяния электронов на колеблющихся с меньшей амплитудой атомах кристаллической решётки. Таким образом даже при абсолютном нуле электроны проводимости движутся между атомами со скоростью Ферми порядка 1×10 6 м/с.
Температура, при которой частицы вещества имеют минимальное количество движения, сохраняющееся только благодаря квантовомеханическому движению, — это температура абсолютного нуля (Т = 0К).
Температура с термодинамической точки зрения
Существует множество различных шкал температур. Когда-то температура определялась очень произвольно. Мерой температуры служили метки, нанесённые на равных расстояниях на стенах трубочки, в которой при нагревании расширялась вода. Потом решили измерить температуру ртутным термометром и обнаружили, что градусные расстояния не одинаковы. В термодинамике дается определение температуры, не зависящее от каких-либо частных свойств вещества.


















Поскольку найденная функция возрастает с температурой, то можно считать, что она сама по себе измеряет температуру, начиная со стандартной температуры в один градус. Это означает, что можно найти температуру тела, определив количество тепла, которое поглощается тепловой машиной, работающей в интервале между температурой тела и температурой в один градус. Полученная таким образом температура называется абсолютной термодинамической температурой и не зависит от свойств вещества. Таким образом, для обратимой тепловой машины выполняется равенство:

Для системы, в которой энтропия



Температура и излучение
При повышении температуры растёт энергия, излучаемая нагретым телом. Энергия излучения абсолютно чёрного тела описывается законом Стефана — Больцмана
Шкала Реомюра
Единица — градус Реомюра (°R), 1 °R равен 1/80 части температурного интервала между опорными точками — температурой таяния льда (0 °R) и кипения воды (80 °R)
Переходы из разных шкал
| в\из | Кельвин | Цельсий | Фаренгейт |
|---|---|---|---|
| Кельвин (K) | = K | = С + 273,15 | = (F + 459,67) / 1,8 |
| Цельсий (° C) | = K − 273,15 | = C | = (F − 32) / 1,8 |
| Фаренгейт (°F) | = K · 1,8 − 459,67 | = C · 1,8 + 32 | = F |
Сравнение температурных шкал
| Описание | Кельвин | Цельсий | Фаренгейт | Ранкин | Делиль | Ньютон | Реомюр | Рёмер |
|---|---|---|---|---|---|---|---|---|
| Абсолютный ноль | 0 | −273.15 | −459.67 | 0 | 559.725 | −90.14 | −218.52 | −135.90 |
| Температура таяния смеси Фаренгейта ( соль и лёд в равных количествах) | 255.37 | −17.78 | 0 | 459.67 | 176.67 | −5.87 | −14.22 | −1.83 |
| Температура замерзания воды (Нормальные условия) | 273.15 | 0 | 32 | 491.67 | 150 | 0 | 0 | 7.5 |
| Средняя температура человеческого тела ¹ | 310.0 | 36.6 | 98.2 | 557.9 | 94.5 | 12.21 | 29.6 | 26.925 |
| Температура кипения воды (Нормальные условия) | 373.15 | 100 | 212 | 671.67 | 0 | 33 | 80 | 60 |
| Плавление титана | 1941 | 1668 | 3034 | 3494 | −2352 | 550 | 1334 | 883 |
| Поверхность Солнца | 5800 | 5526 | 9980 | 10440 | −8140 | 1823 | 4421 | 2909 |
Накопительный водонагреватель
Накопительный водонагреватель, или бойлер (от англ. boiler) представляет собой сравнительно большую ёмкость с размещенным в ней или, реже, под ней, источником тепла. Нагрев может производиться при помощи парового или водяного теплообменника — в нём циркулирует горячая вода в замкнутом контуре, нагреваемая, например, с помощью отопительного котла. Такие бойлеры называют бойлерами (водонагревателями) косвенного нагрева. [2]
Некоторые значения в этой таблице были округлены.
Характеристика фазовых переходов
Для описания точек фазовых переходов различных веществ используют следующие значения температуры:
Измерение температуры
Для измерения температуры выбирается некоторый термодинамический параметр термометрического вещества. Изменение этого параметра однозначно связывается с изменением температуры. На практике для измерения температуры используют
Основное уравнение МКТ идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Идеальный газ — газ, удовлетворяющий трем условиям:
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
Если особо важна точность, следует использовать более точную формулу:
Пример №1. Температура воды равна o C. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p — давление идеального газа, n — концентрация молекул газа, − E k — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
m 0 — масса одной молекулы газа;
n — концентрация молекул газа;
− v 2 — среднее значение квадрата скорости молекул газа.
Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:
k — постоянная Больцмана (k = 1,38∙10 –3 Дж/кг)
T — температура газа по шкале Кельвина
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
Температура — мера кинетической энергии молекул идеального газа:
Полная энергия поступательного движения молекул газа определяется формулой:
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
Составим систему уравнений:

Алгоритм решения
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Основное уравнение МКТ газов. Температура
Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).
В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
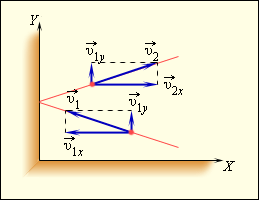
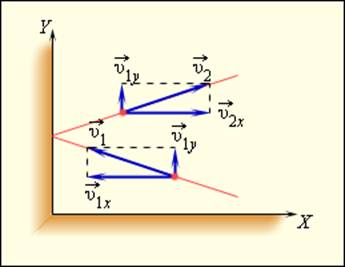
Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной (рис. 3.2.1).
Упругое столкновение молекулы со стенкой
Поэтому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы.
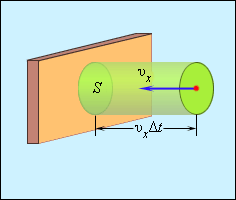
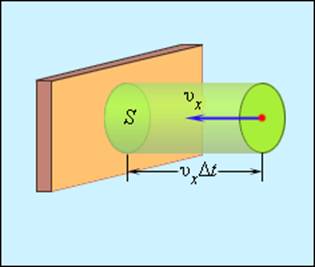
Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υx, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.
Определение числа столкновений молекул с площадкой S
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυxΔt. Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку S за время Δt равно
Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m0υx, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно
По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:
Разделив обе части на SΔt, получим:
где p – давление газа на стенку сосуда.
При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.
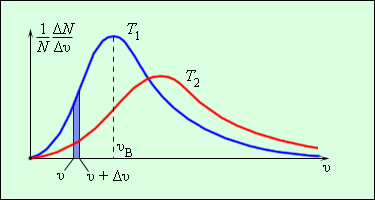
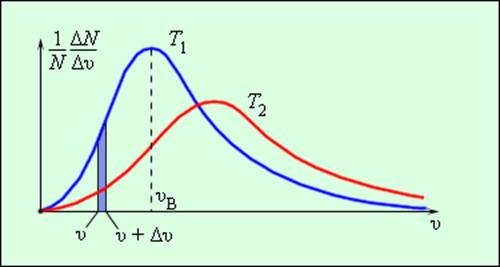
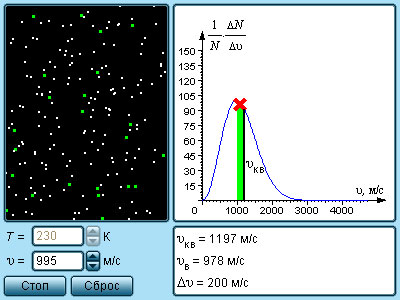
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла. Джеймс Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 3.2.3 столбика.
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υв, соответствующая максимуму кривой распределения, и среднеквадратичная скорость
– среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υв и υкв увеличиваются.


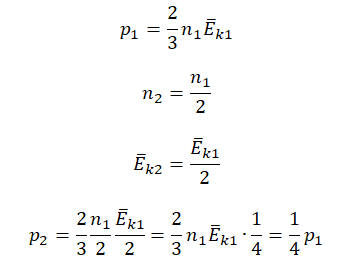
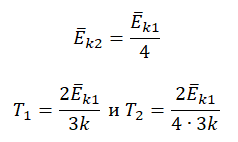
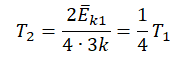
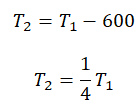
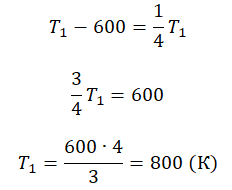
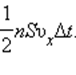
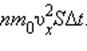
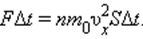
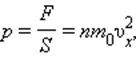
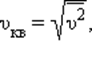

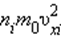

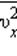 квадрата проекции
квадрата проекции 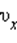 скорости молекул:
скорости молекул:
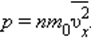
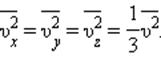
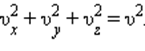
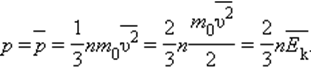
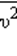 и средней кинетической энергией
и средней кинетической энергией 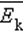 поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.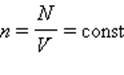
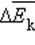 средней кинетической энергии.
средней кинетической энергии.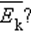 Опыт показывает, что такой величиной является температура.
Опыт показывает, что такой величиной является температура.