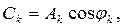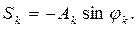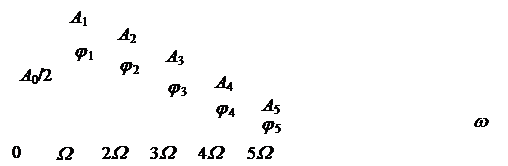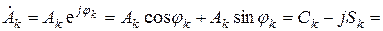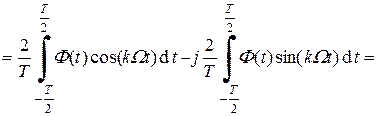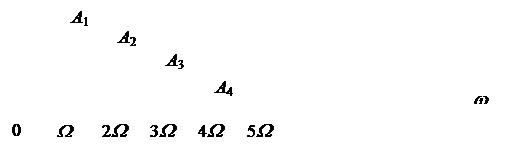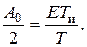Чем определяется спектр периодического сигнала

13.04.202213.04.2022 admin 0 Comments

Спектры периодических сигналов

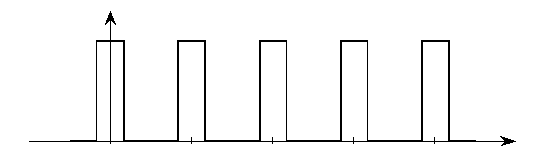
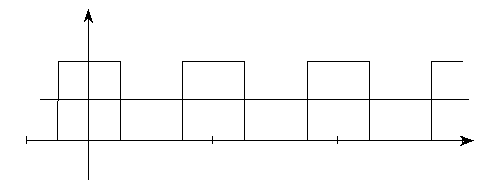
Наиболее просто можно определить спектр периодического сигнала. Напомним, что периодическим называется сигнал Ф(t) (рис. 2.1), удовлетворяющий следующему условию:

Чем определяется спектр периодического сигнала. Смотреть фото Чем определяется спектр периодического сигнала. Смотреть картинку Чем определяется спектр периодического сигнала. Картинка про Чем определяется спектр периодического сигнала. Фото Чем определяется спектр периодического сигнала

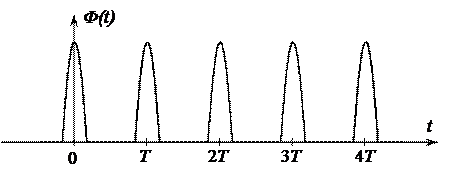Ф(t) = Ф(t + nT), где n – целое число, Т – период повторения.

Рис. 2.1. Периодический сигнал

Из курса математики известно, что всякую периодическую функцию можно представить в виде ряда Фурье:

, (2.1)

, (2.2)

, (2.3)

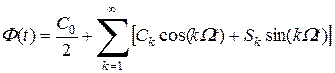
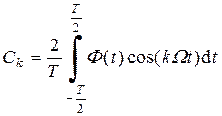
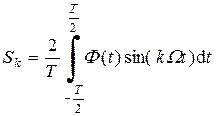
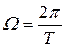
Обычно используется более удобная форма записи ряда Фурье:

(2.4)

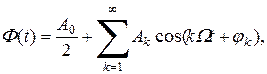
где .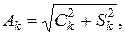

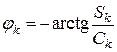
Соответственно,

Рис. 2.2. Спектральная диаграмма периодического сигнала

Составляющая спектра с нулевой частотой называется постоянной составляющей; составляющая с частотой W (основной частотой) – первой гармоникой; составляющая с частотой 2W – второй гармоникой и так далее.

Ряд Фурье может быть записан в комплексной форме. Для этого в выражении (2.4) заменим косинус его представлением по формуле Эйлера:

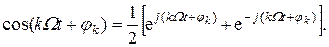
В результате получим

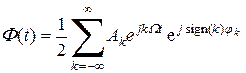
Перейдем к комплексным амплитудам. Обозначим

– для отрицательных значений k.

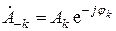
В результате получим окончательное выражение для ряда Фурье в комплексной форме:

(2.5)

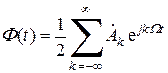
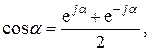
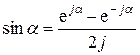
Таким образом, ряд Фурье в комплексной форме также описывает разложение периодической функции на гармонические составляющие, только форма записи здесь иная.

Найдем выражение для определения комплексных амплитуд гармоник A_k. Для этого воспользуемся выражениями (2.2), (2.3):

(2.6)

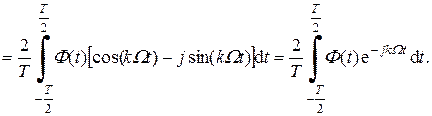
Как будет видно из дальнейших примеров, комплексная форма ряда Фурье часто оказывается предпочтительной для вычисления спектров конкретных периодических сигналов.

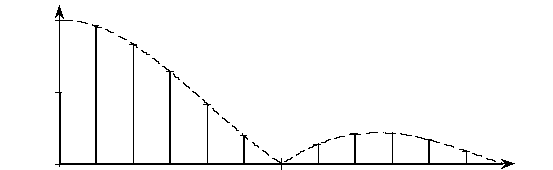
Для удобства построения спектральной диаграммы вводится понятие огибающей спектра:

(2.7)

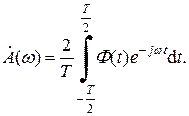
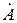
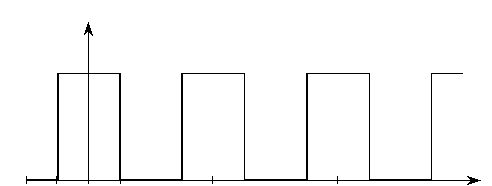
Чтобы построить спектральную диаграмму с помощью огибающей спектра, нужно сначала с помощью формулы (2.7) найти функцию (w), построить ее график, как показано на рис. 2.3, и затем расставить спектральные линии на расстоянии W = 2p/Т друг от друга.

Рассмотрим в качестве примера построение спектральной диаграммы периодической последовательности прямоугольных импульсов, длительностью Т_и и амплитудой Е (рис. 2.4).

Рис. 2.3. Использование огибающей спектра A(w) для построения
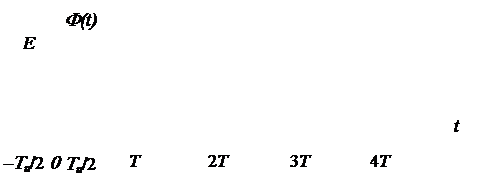
спектральной диаграммы

Рис. 2.4. Периодическая последовательность прямоугольных импульсов

Найдем огибающую спектра:

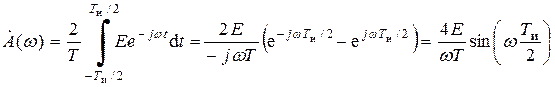
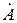
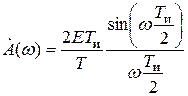
Для удобства построения графика огибающей спектра полученное выше выражение для (w) преобразуем к следующему виду:

. (2.8)

Огибающая спектра А(w) является вещественной функцией, ее график представлен на рис. 2.5 штриховой линией. Характерной точкой графика является значение частоты w, при котором огибающая спектра впервые обращается в нуль. Это происходит, когда аргумент синуса равен p и, следовательно, частота
w = 2p/Т_и.

Рис. 2.5. Спектр периодической последовательности прямоугольных импульсов

Подставив в (2.8) значение частоты первой гармоники W = 2p/Т, найдем амплитуду первой гармоники:

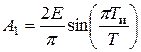
Аналогично для k-й гармоники

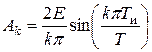
Величина постоянной составляющей А₀/2 вычисляется отдельно по формуле

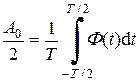
В нашем случае

Нетрудно видеть, что величина постоянной составляющей не равна значению огибающей спектра при w = 0, она выпадает из общей тенденции изменения амплитуд гармоник. Такая особенность спектра характерна для большинства периодических сигналов.

Необходимо отметить, что спектральное представление сигналов – не математическая абстракция, а отражение реально существующего явления. Если взять реальные гармонические сигналы с соответствующими амплитудами и фазами и сложить их, то в результате суммирования получится исходный сигнал, например, периодическая последовательность прямоугольных импульсов.

Это легче всего продемонстрировать на примере периодической последовательности прямоугольных импульсов, у которой интервал между импульсами равен длительности импульсов, т. е. Т = 2Т_и. Такой сигнал, изображенный на рис. 2.6, называется меандром. Найдем амплитуды основных гармонических составляющих меандра:

….

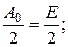
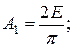
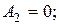
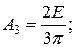
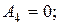
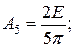
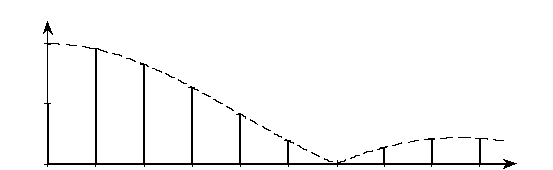
На рис. 2.7, а, б, в последовательно показаны постоянная составляющая плюс первая гармоника; сумма постоянной составляющей и первых трех гармоник; сумма постоянной составляющей и первых пяти гармоник. Хорошо видно, как с увеличением числа гармоник форма сигнала приближается к меандру.

Ф(t)

Рис. 2.7. Представление меандра суммой постоянной составляющей и первой гармоники (а),

суммой постоянной составляющей и первых трех гармоник (б), суммой постоянной

составляющей и первых пяти гармоник (в)

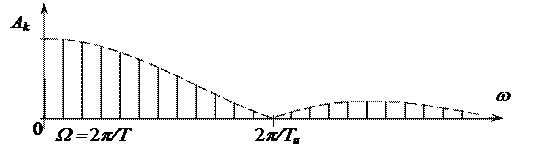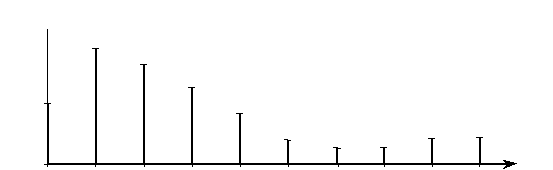
Рассмотрим, как зависит характер спектра от параметров периодической последовательности импульсов. Если увеличить (или уменьшить) длительность импульсов Т_и, то сожмется (или вытянется) по частоте огибающая спектра; положение спектральных линий при этом не изменится. Если же увеличивать расстояние между импульсами, т. е. период повторения Т, не изменяя размеров и формы каждого отдельного импульса, то расстояние между отдельными спектральными составляющими и их высота будут уменьшаться обратно пропорционально периоду повторения Т (рис. 2.8). Эту закономерность мы будем использовать в дальнейшем для определения спектров отдельных импульсов.

Рис. 2.8. Спектр периодического сигнала при увеличенном периоде повторения Т

Источник

2.2. СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

В соответствии со спектральным способом анализа прохождения сигналов через линейные цепи любой случайный сигнал S(T) можно представить в виде бесконечной суммы элементарных аналитически однотипных детерминированных сигналов :

(2.8)

Подавая на вход линейной цепи (рис. 1.14), коэффициент передачи которой равен , элементарный детерминированный сигнал, можно найти элементарный отклик цепи, то есть сигнал на выходе цепи.

Рис.2.3.К определению сигнала на выходе линейной цепи.

Сигнал на выходе линейной цепи равен

(2.9)

Поскольку для линейных цепей справедлив принцип суперпозиции, то результирующий отклик будет равен:

(2.10)

Функции, описывающие элементарные сигналы, называются базисными функциями. Представление сигнала базисными функциями упрощается, если они являются ортогональными и ортонормированными.

Набор функций называется ортогональным, Если в интервале от до

при (2.11)

И ортонормированным, Если для всех Выполняется условие

. (2.12)

Ортогональность базисных функций, с помощью которых представляется исходный сигнал , является гарантией того, что представление сигнала может быть сделано единственным образом. Условию ортогональности отвечают гармонические функции кратных частот, а также функции Уолша, которые на отрезке своего существования от до принимают лишь значения, равные 1, дискретные сигналы Баркера и некоторые другие функции. Спектральный метод анализа сигналов основан на преобразованиях Фурье и состоит в замене сложной функции времени, описывающей сигнал, суммой простых гармонических сигналов, образующих частотный спектр этого сигнала. Знаменитый французский физик и математик Ж. Б. Фурье (1768 – 1830 г. г.) доказал, что любое изменение во времени некоторой функции можно аппроксимировать в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Этой функцией может быть ток или напряжение в электрической цепи.

Рассмотрим вначале представление периодического электрического сигнала (рис. 2.4), отвечающего условию

, (2.13)

где: — период сигнала; =1,2,3,….

Рис. 2.4. Периодический сигнал

Представим этот сигнал бесконечным тригонометрическим рядом:

. (2.14)

Этот ряд называется рядом Фурье.

Возможна запись ряда Фурье в другом виде:

, (2.15)

Где: — модуль амплитуд гармоник;

— фазы гармоник;

— круговая частота;

— коэффициенты косинусоидальных составляющих; — коэффициенты синусоидальных составляющих; — среднее значение сигнала за период (постоянная составляющая).

Отдельные слагаемые рядов называют гармониками. Число является номером гармоники. Совокупность величин в ряде (2.15) называют спектром амплитуд, а совокупность величин — спектром фаз.

Ниже на рис. 2.5 представлены амплитудный и фазовый спектры периодического сигнала. Вертикальные отрезки амплитудного спектра представляют амплитуды гармоник и называются спектральными линиями.

Рис 2.5. Амплитудный и фазовый спектры периодического сигнала

Таким образом, спектр периодического сигнала – Линейчатый. Каждый периодический сигнал имеет вполне определенные амплитудный и фазовый спектры.

Сумма ряда (2.15) является бесконечной, но, начиная с некоторого номера, амплитуды гармоник настолько малы, что ими можно пренебречь и практически реальный периодический сигнал представляется функцией с ограниченным спектром. Интервал частот, соответствующий ограниченному спектру, называется шириной спектра.

Если функция , описывающая периодический сигнал, является четной, то сумма ряда (2.14) будет содержать только косинусоидальные составляющие. Если — нечетная функция, то сумма будет содержать только синусоидальные составляющие.

Возможно также представление периодического сигнала в виде комплексного ряда Фурье:

, (2.16)

— комплексные амплитуды спектра, содержащие информацию, как об амплитудном, так и о фазовом спектрах.

После подстановки значений и , получим:

(2.17)

Если подставить полученное значение в ряд (1.29), то он обращается в тождество. Таким образом, периодический электрический сигнал можно задавать либо функцией времени , либо комплексной амплитудой спектра.

2.2.1. Спектр периодической последовательности прямоугольных импульсов

Рис.2.6.Периодические последовательности импульсов и их спектры.

2.2.2. Спектр непериодического сигнала

При рассмотрении спектра непериодического сигнала воспользуемся предельным переходом от периодического сигнала к непериодическому сигналу, устремив период к бесконечности.

Для периодического сигнала, представленного на рис. 2.4, ранее получено выражение (2.17) для комплексной амплитуды спектра:

(2.18)

(2.19)

Построим модуль спектра :

Рис. 2.7. Модуль спектра периодического сигнала

Рис. 2.8. Спектр непериодического сигнала

При этом комплексная амплитуда равна:

. (2.20)

С учетом предельного перехода при

(2.21)

Подставим полученное выражение в ряд (2.16). При этом сумма трансформируется в интеграл, а значения дискретных частот в значение текущей частоты и непериодический сигнал можно представить в следующем виде:

. (2.22)

Это выражение соответствует обратному преобразованию Фурье. Огибающая сплошного спектра одиночного импульса совпадает с огибающей линейчатого спектра периодической функции, представляющей периодическое повторение этого импульса.

Интеграл Фурье позволяет любую непериодическую функцию представить в виде суммы бесконечного числа синусоидальных колебаний с бесконечно малыми амплитудами и бесконечно малым интервалом по частоте. Спектр сигнала определяется из выражения

. (2.23)

Этот интеграл соответствует прямому преобразованию Фурье.

– комплексный спектр, в нём содержится информация, как о спектре амплитуд, так и о спектре фаз.

Таким образом, спектр непериодической функции сплошной. Можно сказать, что в нём содержатся «все» частоты. Если вырезать из сплошного спектра малый интервал частот , то частоты спектральных составляющих в этом участке будут отличаться сколь угодно мало. Поэтому спектральные составляющие можно складывать так, как будто все они имеют одну и ту же частоту и одинаковые комплексные амплитуды. Спектральная плотность есть отношение комплексной амплитуды малого интервала частот к величине этого интервала.

Спектральный анализ сигналов имеет фундаментальное значение в радиоэлектронике. Информация о спектре сигнала позволяет обоснованно выбирать полосу пропускания устройств, на которые воздействует этот сигнал.

2.2.3. Спектр одиночного прямоугольного видеоимпульса

Рассчитаем спектр одиночного прямоугольного импульса, амплитуда которого равна Е, а длительность — t, представленного на рис. 2.9.

Рис. 2.9. Одиночный прямоугольный импульс

В соответствии с выражением (2.24) спектр такого сигнала равен

=. (2.24)

На рис. 2.10 представлен комплексный спектр одиночного прямоугольного импульса длительностью .

Рис.2.10. Спектр одиночного прямоугольного импульса

Спектральная плотность определяет распределение энергии в спектре одиночного импульса. В общем случае распределение энергии неоднородно. Однородное распределение характерно для хаотического процесса, называемого «белым шумом».

Спектральная плотность импульса на нулевой частоте равна его площади. Приблизительно 90% энергии одиночного прямоугольного импульса сосредоточено в спектре, ширина которого определяется выражением

. (2.25)

Соотношение (1.41) определяет требования к ширине полосы пропускания радиотехнического устройства. В задачах, где форма сигнала имеет второстепенное значение полосу пропускания устройства для этого сигнала можно выбрать равной ширине первого лепестка спектра. При этом неизвестна степень искажения формы сигнала. Двукратное увеличение полосы пропускания лишь на 5% увеличит энергию сигнала при одновременном возрастании уровня шумов.

2.2.4. Спектры неинтегрируемых сигналов

Фурье анализ применим лишь к интегрируемым функциям, то есть к функциям, для которых выполняется условие сходимости интеграла:

(2.26)

К неинтегрируемым относятся такие сигналы, как -импульс, единичный скачок, гармонический сигнал, постоянное напряжение.

Спектр — импульса

Рассчитаем спектр —Импульса с помощью интеграла прямого преобразования Фурье.

(2.27)

На основании стробирующего свойства — функции получим:

. (2.28)

Таким образом, и . При фаза .

Рис.2.11. Спектр — импульса

Итак, — функция имеет сплошной бесконечный спектр с единичной амплитудой на всех частотах. В момент возникновения импульса все гармонические составляющие бесконечного спектра складываются когерентно, поскольку спектр вещественный. В результате этого наблюдается бесконечно большая амплитуда импульса.

Спектр гармонического сигнала

Вычислим спектр гармонического сигнала с единичной амплитудой .