Чем определяется сопротивление металлов при температурах выше температуры дебая
Металлические термометры сопротивления. Для металлов при температурах, близких к температуре Дебая и выше, удельное сопротивление ρ линейно меняется с температурой Т
Для металлов при температурах, близких к температуре Дебая и выше, удельное сопротивление ρ линейно меняется с температурой Т
где ρ0 и αρ – удельное сопротивление и температурный коэффициент удельного сопротивления.
αρ = 1/ρ·(dρ/dT) при температуре Т0. Это объясняется рассеиванием электронов на фононах.
Температурный коэффициент сопротивления (ТКС)
зависит от αρ и от коэффициента линейного расширения материала αL: αR = αρ – αL. Ввиду того, что αL на два порядка меньше, чем αρ, то αR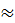 
αρ.
При небольших изменениях температуры ΔТ в окрестности значения Т зависимость сопротивления металлического резистора от температуры линейна
В более широком диапазоне температур
R(T) = R0 (1 + AT + BT 2 + CT 3 ), (3.4)
где Т выражается в градусах Цельсия; R0 – сопротивление при 0 ºС.
Для измерения температуры используются терморезисторы с высокостабильным ТКС, линейной зависимостью R(T), хорошей воспроизводимостью свойств и инертностью к воздействию окружающей среды. К таким материалам в первую очередь относится платина. Из-за дешевизны используются медные терморезисторы, а также применяются вольфрамовые и никелевые. Платину можно получить очень высокой чистоты (99,999 %), химическая пассивность платины и отсутствие структурных изменений обеспечивают стабильность электрических свойств. Платиновые термометры сопротивления используются а диапазоне от –260 до 1100 ºС.
Зависимость сопротивления меди от температуры линейна с очень высокой степенью точности, но химическая активность меди ограничивает верхний температурный предел 180 ºС. Нижний температурный предел составляет –200 ºС. Из-за низкого удельного сопротивления меди приходится использовать длинные проводники.
У терморезисторов из вольфрама наблюдается большая чувствительность к низким температурам ( при менее 100 К), чем у платины. Вольфрам может примеряться при более высоких температурах, чем платина, и имеет лучшую линейность сопротивления. Недостатком его является худшая стабильность электрических характеристик, чем у платины.
Дата добавления: 2015-02-16 ; просмотров: 712 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Температурная зависимость удельного сопротивления металлических проводников
Лабораторная работа № 10
Исследование проводниковых материалов
Цель работы
1. Изучить процессы, протекающие в проводниках в электрическом поле.
2. Исследовать основные свойства проводников по температурным зависимостям проводимости.
Основные теоретические положения
Электроны в металлах
К твердым проводникам относятся металлы (металлические материалы)
По величине удельного сопротивления р металлические проводники делятся на следующие группы:
— металлы и сплавы с высокой удельной проводимостью γ
— металлы и сплавы со средним значением ρ;
— металлы и сплавы с высоким значением ρ.
Металлические проводники – основной тип проводниковых материалов, применяемых в микроэлектронике. Согласно классической электронной теории в металлах есть электронный газ, представленный свободными электронами. Именно электрон в металле переносит электронный заряд. Под действием электрического поля электроны приобретают направление (хаотическое) движение, что получило выражение в законе Ома, законе Джоуля-Ленца.
где, 
– скорость теплового движения электрона
– средняя длина свободного пробега
– масса покоя электрона
– напряженность электрического поля
Электроны обладают определенным значением энергии, тем самым распределяются по энергетическим состояниям (уровням). В квантовой теории максимальное значение энергии, которую может иметь электрон в металле при температуре абсолютного нуля называют энергией Ферми или уровнем Ферми.
При изменении температуры энергия Ферми 
изменяется незначительно, что является спецификой вырожденного состояния электронного газа. Например, при нагревании серебра от 0 до 1000 К энергия Ферми у него уменьшается лишь на 0,2 %. Столь малые изменения в таком широком температурном диапазоне можно не учитывать.
Таким образом, проводимость определяется, в основном, средней длиной свободного пробега электронов, которая, в свою очередь, зависит от структуры проводника, т.е. химической природы атомов, элктронно-ядерной структурной организации и типа кристаллической решетки.
Температурная зависимость удельного сопротивления металлических проводников
В идеальном кристалле длина свободного пробега электронов равна бесконечности, а сопротивление электрическому току равно нулю.
В теории колебаний атомных остовов решетки следует учитывать не только амплитуду колебаний, но и частоту. Так, максимальная частота тепловых колебаний определяется температурой Дебая Ɵд.
Эта температура зависит от длины и энергии связи между атомными остовами в узлах кристаллической решетки и является важным параметром твердого тела.
При Т > Ɵд. удельное сопротивление металлов изменяется линейно с температурой (рис. 1. участок III).
Для большинства металлов характеристическая температура Дебая не превышает 400-450 К. Поэтому линейное приближение обычно справедливо при температурах от комнатной и выше. В низкотемпературной области (Т
( 
, м)
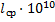
В пределах переходной области II происходит быстрый рост удельного сопротивления ρ (Т), где n может быть до 5 и постепенно убывает с ростом температуры
Линейный участок (область III) в температурной зависимости ρ (T) у большинства металлов простирается до температур, близких к точке плавления. Исключение из этого правила составляют ферромагнитные металлы, в которых имеет место дополнительное рассеяние электронов на нарушениях спинового порядка. Вблизи точки плавления, т.е. в области IV, в обычных металлах может наблюдаться некоторое отступление от линейной зависимости.
Относительное изменение удельного сопротивления при изменении температуры на один кельвин (градус) называют температурным коэффициентом удельного сопротивления:
Правило Маттиссена об аддитивности удельного сопротивления:
т е. полное удельное сопротивление металла есть сумма удельного сопротивления, обусловленного рассеянием электронов на тепловых колебаниях узлов кристаллической решетки, и остаточного удельного сопротивления, обусловленного рассеянием электронов на статических дефектах структуры.
Рис. 2. Температурные зависимости удельного сопротивления сплавов меди типа твердых растворов, иллюстрирующие правило Матиссена: 1 – чистая Cu; 2 – Cu – 1,03 ат. % In; 3 – Cu – 1,12 ат. % Ni
Чем определяется сопротивление металлов при температурах выше температуры дебая
Рис. 10.5. Зависимость удельного сопротивления металла от температуры
Проведем качественный анализ температурной зависимости удельного сопротивления металлов. Электронный газ в металлах является вырожденным и основным механизмом рассеяния электронов в области высоких температур является рассеяние на фононах.
При достижении температуры плавления и переходе в жидкое состояние у большинства металлов наблюдается резкое увеличение удельного сопротивления и у некоторых его уменьшение. Если плавление металла или сплава сопровождается увеличением объема, то удельное сопротивление повышается в два–четыре раза (например, у ртути в 4 раза).
Важной характеристикой металлов является температурный коэффициент удельного электрического сопротивления, показывающий относительное изменение удельного сопротивления при изменении температуры на один Кельвин (градус)
ar— положительно, когда удельное сопротивление возрастает при повышении температуры. Очевидно, что величина ar также является функцией температуры. В области 3 линейной зависимости r ( T ) (см. рисунок 10.3) выполняется соотношение:
Остаточное удельное сопротивление металлов. Как говорилось выше, сопротивление нормальных металлов стремится к постоянному значению — остаточному сопротивлению, по мере снижения температуры до абсолютного нуля. У нормальных металлов (не сверхпроводников) остаточное сопротивление возникает из-за рассеяния электронов проводимости статическими дефектами
Обширный экспериментальный материал содержит многочисленные данные по измерению сопротивления в металлах, вызванному наличием в них примесей. Можно отметить следующие наиболее характерные изменения в металлах, вызываемые легированием. Во-первых, не считая фононных возмущений, примесь является локальным нарушением идеальности решетки совершенное во всех других отношениях. Во-вторых, легирование влияет на зонную структуру, сдвигая энергию Ферми и изменяя плотность состоянии и эффективную массу, т.е. параметры, частично определяющие идеальное сопротивление металла. В-третьих, легирование может менять упругие константы и, соответственно, колебательный спектр решетки, оказывая влияние на идеальное сопротивление.
СВЯЗЬ ПРОЧНОСТНЫХ ХАРАКТЕРИСТИК МЕТАЛЛОВ С ТЕМПЕРАТУРОЙ ДЕБАЯ
Хентов В.Я.
Профессор, доктор химических наук,
Южно-Российский государственный политехнический университет имени М.И. Платова
СВЯЗЬ ПРОЧНОСТНЫХ ХАРАКТЕРИСТИК МЕТАЛЛОВ С ТЕМПЕРАТУРОЙ ДЕБАЯ
Аннотация
Показано, что такие прочностные характеристики металлов, как модуль упругости Юнга, модуль сдвига, сжимаемость и энергия активации разрушения металлов, тесно связаны с температурой Дебая металлического элемента.
Ключевые слова: модуль упругости Юнга, модуль сдвига, сжимаемость элементов, прочность проволоки на разрыв, энергия активации разрушения металлов, температура Дебая.
Khentov V.Ya
South-Russian State Polytechnic University named after M. Platov
COMMUNICATION STRENGTH CHARACTERISTICS METAL DEBYE TEMPERATURE
Abstract
It is shown that the strength properties of metals such as Young’s modulus, shear modulus, compressibility, and the activation energy of fracture of metals are closely related to the Debye temperature of the metal element.
Keywords: Young’s modulus, shear modulus, compressibility elements breaking strength of the wire, the activation energy of fracture of metals, the Debye temperature.
Прочность является важнейшим физическим свойством твердого тела. Представления о прочности тесно связаны со спецификой межатомного и межмолекулярного взаимодействия. Рассчитанные с учетом этого значения прочности заметно превосходят реальную технологическую прочность материалов, что связывают с дефектами кристаллической решетки и наличием микротрещин [1, 2]. Особый интерес вызывает разработка теории разрушения кристаллических твердых тел. Процесс разрушения носит кинетический и статистический характер, а также является многостадийным. Вместе с тем, теория разрушения должна базироваться на физических и химических свойствах твердого тела. В ряде работ [3, 4] была установлена связь физических свойств твердого тела с температурой Дебая. В настоящей работе приведены корреляционные зависимости прочностных характеристик твердого тела с температурой Дебая металла [5]. Основные корреляционные уравнения представлены в табл. 1.
Таблица 1 ‒ Корреляционные зависимости, коэффициенты корреляции R
| Прочностной параметр | Корреляционная зависимость | R | Металлы | |||
| 1 | 2 | 3 | 4 | |||
| Вектор Бергерса b [6] | b=0,2055-0,0001Θ | 0,86 | Pb, Al, Ag,Cu, Ni, [7] | α=710,683-20,391Θ | 0,94 | Fe, Cu, Ni, Sn, Pb, Ag, Zn |
| Коэффициент Пуас-сона μ [7] | μ=1112,7-2339,2Θ | 0,74 | Al, Be, V, Bi, W, Gd, Hf, Dy, Fe, Au, In, Ir, Y, Cd, Co, La, Li, Mg, Cu, Mo, Ni, Nb, Sn, Os, Pd, Pt, Pb, Ag, Ta, Ti, Cr, Zr, Zn | |||
| Cжимаемость элемен-тов k∙10 6 [8] | k=528,406-85,261Θ | 0,93 | Fe, Cd, Mn, Cu, Mo, Ni, Sn, Pb, Ag, Tl | |||
| Предел прочности, σв, МПа [7] | σв=163,53+0,66Θ | 0,87 | V, Fe, Au, Y, Cd, Ca, Co, Mg, Cu, Ni, Nb, Sn, Pd, Pt, Re, Pb, Ag, Sc, Rh, Ru | |||
| Твердость по Бринел-лю, НВ, МПа [7] | НВ=-749,06+4,82Θ | 0,83 | V, Bi, Fe, Au, Ir, Co, Cu, Mo, Ni, Nb, Sn, Pd, Pt, Re, Ru, Ag, Sc, | |||
| Энергия активации разрушения металла, Еа, кДж/моль (рассчитана по данным [9]) | Еа=2,820+0,055Θ | 0,99 | Al, Cd, Fe, Sn, Pb | |||
| Истинная теоретичес-кая прочность, Sпр, ГПа [11] | Sпр=-6,777+0,0731Θ | 0,95 | Fe, Ni, Cu, Ti, Ag, V, Mo, Cd, Na, K | |||
| Характеристика кри-тической деформа-ции* εf [10] | εf=0,4794-0,0003Θ | 0,89 | Fe, W, Mo, Nb, V | |||
| Плотность энергии связи атомов p0 в объеме одного моля V0 вещества p0=Qc/V0, где V0=A/D, А ‒ атомная масса, D ‒ плотность [10] | р0=-10,543+0,0976Θ | 0,98 | Al, Cr, Zn, Cd, K, Na | |||
| Модуль сдвига (экспе-римент) G, Гпа [10] | G=-13,233+0,1808Θ | 0,94 | Fe, Au, Cr, Ti, Zn, K, Na | |||
| Модуль упругости Юнга (эксперимент) Е, ГПа [10] | E=-45,0134+0,5115Θ | 0,94 | Fe, Ni, Ti, Au, Ag, Cr, Zn, Na, K | |||
| Теоретическая проч-ность на сдвиг τтеор, ГПа [10] | τтеор=-3,109+0,043Θ | 0,94 | Fe, Au, Cr, Ti, Zn, K, Na | |||
| Поверхностная энер-гия металла (расчет) γ, Дж/м 2 [10] | γ=0,2386+0,0025Θ | 0,88 | Ag, Ni, Cu, Fe, Ti, Au, Mo, Pb | |||
| Постоянная материала в формуле 1.105 [10], Примечания: *критическая деформация непосредственно связана с разрывом атомных связей. Необходимо отметить, что для узкого ряда металлов могут быть получены идеальные корреляционные зависимости. Рис. 1 иллюстрирует для свинца, серебра, меди, никеля и α-железа зависимость коэффициента Пуассона от температуры Дебая с высоким значением коэффициента корреляции – 0,97. Для свинца, серебра, меди и α-железа коэффициент корреляции достигает значения 0,99. К сожалению этот факт пока не находит объяснения.
Рис. 1 – Зависимость коэффициента Пуассона [6] от температуры Дебая металла. Коэффициент корреляции 0,97 Металлы: 1 – Pb, 2 – Ag, 3 – Cu, 4 – Ni, 5 ‒ α-Fe На рис. 2 приведена зависимость прочности проволоки на разрыв (усредненные значения) [8] от температуры Дебая металла.
Рис. 2 – Зависимость прочности проволоки на разрыв от температуры Дебая металла. Коэффициент корреляции 0,96 На рис. 3 приведена зависимость изотермической сжимаемости химических элементов К (Ba, V, Bi, Hf, Fe, In, Y, Cd, K, Ca, Co, La, Cu, Na, Ni, Nb, β-Sn, Pb, Se, Ag, Sr, Sb, Tl, Tc, Ti, Zn, Zr) [7] от температуры Дебая металла. Рис. 4 демонстрирует зависимость экспериментальной величины всестороннего модуля сжатия Ксж [10] от температуры Дебая металла. Эта зависимость для указанных металлов характеризуется высоким значением коэффициента корреляции – 0,99.
Рис. 3 – Зависимость изотермической сжимаемости химических элементов К от температуры Дебая металла. Коэффициент корреляции 0,87
Рис. 4 – Зависимость экспериментальной величины всестороннего модуля сжатия Ксж от температуры Дебая металла Металлы: 1 – K, 2 – Na, 3 – Cd, 4 – Zn, 5 – Al Литература Температурная зависимость удельного сопротивления металловРассмотрим движение свободных электронов в виде плоских электронных волн, длина которых λ определяется соотношением де Бройля (1.3). Такая электронная волна распространяется в строго периодическом потенциальном поле без рассеяния энергии. Это означает, что в идеальном кристалле длина свободного пробега электронов равна бесконечности, а сопротивление электрическому току равно нулю. Причинами рассеяния электронов в реальных металлах, создающего электрическое сопротивление, являются: • тепловые колебания узлов кристаллической решетки (ρт тепловая составляющая электрического сопротивления); • примеси и дефекты структуры (ρост составляющая ρ, обусловленная нетепловыми факторами). Известно, что эффективное рассеяние энергии электронов происходит в том случае, если размер рассеивающих центров (дефектов) превышает 1/4 длины волны. В металлах энергия электронов проводимости составляет 3…15 эВ, этой энергии соответствует длина электронной волны λ = 0,3…0,7нм. Поэтому любые микронеоднородности и несовершенства кристаллического строения вызывают снижение проводимости. Итак, удельное сопротивление реальных металлов представляет собой сумму двух составляющих: Относительное изменение удельного сопротивления металлов при изменении температуры характеризует температурный коэффициент удельного сопротивления: Металлы имеют положительное значение αρ, т.е. с ростом температуры ρ увеличивается, что связано с увеличением амплитуды тепловых колебаний узлов кристаллической решетки. Причем удельное сопротивление растет пропорционально температуре. Однако линейная зависимость ρ(Т) нарушается при низких температурах из-за снижения амплитуды и частоты тепловых колебаний атомов. Максимальная частота тепловых колебаний определяет характеристическую температуру температуру Дебая где h постоянная Планка; k постоянная Больцмана. Температурная зависимость удельного сопротивления металлов приведена на рис. 3. В области сверхнизких температур, близких к абсолютному нулю, значение ρ практически не зависит от температуры (участок I) и определяется остаточным сопротивлением ρост. В этой области у некоторых металлов наблюдается состояние сверхпроводимости (Тсв критическая температура сверхпроводимости). В узкой переходной области II (до температуры θD) удельное сопротивление растет по степенной зависимости ρ Tn. Экспериментально установлено, что линейная зависимость ρ(Т) справедлива от Т = 2/3 θD и сохраняется у большинства металлов вплоть до температуры плавления. В области линейной зависимости (III) уделное электрическое сопротивление опреляется по формуле где ρ0 удельное сопротивление при начальной температуре (например, при комнатной Т0 = 293 К).
При переходе из твердого состояния в жидкое у большинства металлов наблюдается резкое увеличение удельного сопротивления (в 1,5…2 раза), связанное с нарушением ближнего порядка в расположении атомов. Исключение составляют висмут, сурьма, галлий, объем которых при плавлении уменьшается, что сопровождается уменьшением удельного сопротивления. В табл. 2 приведены основные характеристики некоторых металлов. Значения характеристик некоторых металлов при 20°С
|
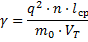
Рис. 3. Температурная зависимость удельного электрического сопротивления металла (1) и сверхпроводника (2)