Чем определяется распределение амплитуд возбуждения поверхности раскрыва зеркала

13.04.202213.04.2022 admin 0 Comments

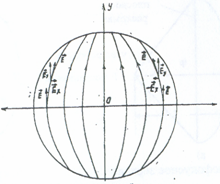
Направленные свойства параболической антенны зависят не только от ее относительных (относительно длины волны) размеров, но и от того, как распределены амплитуды полей в раскрыве. Наиболее высокие направленные свойства реализуются в том случае, когда амплитуда поля по раскрыву постоянна. Однако получить равномерное распределение амплитуды поля по раскрыву нереально. При возбуждении зеркала облучателем наведенные токи текут по вогнутой поверхности. Проекции линий тока на поверхность раскрыва (рис.3) представляют собой семейство кривых. Аналогичную картину в плоскости раскрыва образуют линии напряженности электрического поля. Как видно из рис.3, вектор напряженности электрического поля Е имеет две составляюшие – E_x и E_y, причем составляющие E_x на краях зеркала имеют максимальную амплитуду и диаметрально противоположны по знаку. Поэтому составляющая E_x вдоль фокальной оси не принимает участия в излучении, из–за чего излучающая способность периферии зеркала меньше, чем центральной области.

Рис. 3 Картина поля в раскрыве параболы

Уменьшение амплитуды поля от центра к краям раскрыва эквивалентно уменьшению его размера. Поэтому по сравнению с равноамплитудным распределением ширина главного лепестка ДН увеличивается. Уменьшить неравномерность поля в раскрыве можно за счет увеличения фокусного расстояния зеркала. Однако при этом уменьшается доля энергии облучателя, падающей на зеркало, так как увеличивается « переливание» энергии через край зеркала.

Распределение амплитуды поля по раскрыву зеркала зависит также от направленных свойств облучателя. Чем шире его диаграмма направленности, тем более равномерно поле в раскрыве. При этом неизбежно уменьшается доля энергии, падающая на зеркало. Соответственно, из – за дифракционных эффектов на краю зеркала увеличивается уровень боковых лепестков ДН направленности антенны.

Все вышеизложенное показывает, что при заданном диаметре зеркала для получения максимально узкого главного лепестка ДН нужно применять антенны с большим фокусным расстоянием и ненаправленным облучателем. А для получения максимального КНД необходимо обеспечить определенное соотношение между фокусным расстоянием зеркала и ДН облучателя.

Таким образом, условие максимально узкого главного лепестка ДН антенны и максимального коэффициента направленного действия (КНД) различаются. Поэтому на практике применяются как длиннофокусные антенны (условие максимально узкого лепестка ДН), так и короткофокусные антенны (условие максимального КНД). Длиннофокусные антенны применяют тогда, когда необходима высокая разрешающая способность антенны (в радиоастрономии, радиолокации, в системах наведения), а короткофокусные антенны чаще всего применяют при работе с сигналами малого уровня мощности (космическая радиосвязь и др.)

В качестве облучателя зеркальных антенн обычно применяют слабонаправленные антенны (антенны относительно малых размеров): рупоры, спирали, щелевые излучатели, вибраторы с рефлектором. Диаграмма направленности таких облучателей хорошо аппроксимируется функцией

При этом, если ДН облучателя обеспечивает уменьшение амплитуды напряженности поля на краю зеркала относительно амплитуды поля у его вершины на 10 дБ (0.316 раз), то КНД антенны принимает максимальное значение.

Расчет диаграммы направленности параболической антенны производится на основе закона распределения плотности тока проводимости на поверхности зеркала, либо на основе закона распределения амплитуды поля по раскрыву. Последний метод значительно упрощает процедуру расчетов, но результаты расчета получаются с известными приближениями. Формулы для расчета диаграммы направленности имеют достаточно громоздкий вид. В первом приближении, полагая, что поле в раскрыве синфазно и равноамплитудно, диаграмму направленности антенны можно вычислять по формуле

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

КНД и КУ зеркальных антенн. 13.1 Облучатель зеркал. Приближенный расчет параболической антенн

Лекция 13. КНД и КУ зеркальных антенн.

13.1 Облучатель зеркал. Приближенный расчет параболической антенны.

13. КНД и КУ зеркальных антенн.

а) ,

где — геометрическая площадь, — коэффициент использования поверхности и определяется амплитудой поля в раскрыве зеркала.

(1)

В случае параболических зеркал имеем.

; ; (2)

Подставив (1) в (2) получим

(3)

Для приближенного расчета пренебрегают зависимостью распределения поля от и считают, что амплитуда поля в раскрыве является функцией только координаты , тогда (3) упрощается и принимает вид

Для облучателя в виде диполя с диполевым рефлектором имеет вид.

Рис. 84. Завистимость коэффициента использования поверхности раскрыва от угла раскрыва зеркала.

при – это объясняется тем, что поле очень малых зеркал приблизительно равномерное. С увеличением глубины зеркал быстро уменьшается.

КНД по формуле а) не учитывает потерь энергии на рассеивание, то есть энергии проходящей от облучателя мимо зеркала.

Для более полной характеристики следует использовать такой параметр, как КУ антенны

– КПД

Тепловыми потерями электромагнитной энергии на поврхности зеркала можно пренебречь (они очень малы).

Тогда под следует понимать

где – энергия попадающая на зеркало, – мощность излученная облучателем.

Для определения этого отношения окружим облучатель сферой радиусом элемент поверхности сферы равен

Рис. 85. К определению КПД зеркальной антенны.

Полная мощность облучателя определяется выражением

где – амплитуда напряженности поля в направлении максимального излучения облучателя; нормированная ДН облучателя.

Мощность излучения, попадающего на зеркало.

б)

Из выражения (б) видно, что полностью определяется ДН облучателя и величиной . Очевидно, чем больше , то есть чем глубже зеркало, тем большая часть излученной энергии попадает на зеркало и следовательно, тем больше . Таким образом характер применения противоположен характеру изменения . Опять компромисс.

13.1 Облучатель зеркал. Приближенный расчет параболической антенны.

Ширина диаграммы направленности на уровне половинной мощности 2QН0.5

Тип облучателя: Полуволновый вибратор с дисковым контр рефлектором;

Средняя яркостная температура неба Тнср = 15 К;

Температура шумов приемника Тпр = 2100 К;

Длина фидерной линии lф = 6 м.

1. Расчет геометрических и электродинамических параметров облучателя и параболоида:

1.1 Выбор фидера. Определение шумовой температуры фидерного тракта;

1.2 Определение диаметра раскрыва;

1.3 Определение угла раскрыва и фокусного расстояния зеркальной антенны.

1.3.1 аппроксимация аналитического вида ДН облучателя функцией вида cosn/2Y

2. Расчет геометрических и электродинамических характеристик поля

2.1 диаграммы направленности облучателя

2.2 распределение поля в апертуре зеркала.

3. Расчет пространственной диаграммы направленности и определение параметров параболической антенны

4 Конструктивный расчет антенны:

a) расчет профиля зеркала

b) выбор конструкции зеркала

c) определение допусков на точность изготовления

Список использованной литературы

1. Определение геометрических размеров параболического зеркала

1.1 Выбор фидера. Определение шумовой температуры фидерного тракта Тафу и КПД;

Выбираем фидер РК-75-3-13, т. к. он подходит по частоте f=1 ГГц и обладает наименьшим коэффициентом затухания 0,11

Длина волны определяется по формуле:

Шумовая температура фидерного тракта Тафу определяется по формуле:

где б – коэффициент затухания линии передачи [дБ/м],

lф – длина фидерной линии [м].

КПД определяется по формуле:

Определим шумовую температуру антенной системы:

1.2 Определение диаметра раскрыва

параболическая антенна облучатель поле

Зеркальная антенна – направленная антенна, содержащая первичный излучатель и отражатель антенны в виде металлической поверхности. Параболическая зеркальная антенна представлена на рисунке 1.

В случае равномерно возбуждённого раскрыва параболического зеркала ширина ДН приближённо определяется:

, где

2Q0.5 – ширина диаграммы направленности на уровне половинной мощности, рад.;

R0 – радиус раскрыва зеркала (рисунок 1).

Неравномерное возбуждение раскрыва зеркала приводит к некоторому расширению главного лепестка ДН, так как уменьшается эффективная площадь раскрыва. Чаще всего диаграммы направленности зеркальных антенн не обладают осевой симметрией, т. е. ширина главного лепестка в плоскостях Е и Н различна. В большинстве практических случаев это влечёт за собой следующее изменение:

, где

2QЕ0.5, 2QН0.5 ширина ДН соответственно в плоскостях Е и Н.

Для Е и Н плоскостей соответственно найдем радиус раскрыва:

Т. к. в курсовой имеются данные о ширине диаграммы направленности в обеих плоскостях, можно определить диаметр раскрыва dp = 2 Ч R0, причем из полученных двух значений диаметра следует выбрать наибольшее. Следовательно, R0 = 3,03 (м).

dp = 2 Ч R0 = 2 Ч 3,033 = 6,066 м

1.3 Определение угла раскрыва и фокусного расстояния зеркальной антенны

С точки зрения оптимизации геометрии антенны по максимальному отношению сигнал/шум необходимо произвести следующий расчет.

Чувствительность g определяется формулой:

Где первые четыре коэффициента не зависят от yо, а g’ вычисляется:

, где

u = (0.02 – 0.03) – коэффициент, учитывающий «переливание» части мощности облучателя через края зеркала;

n = 4 – определяется типом облучателя;

S = р Ч R2= 3.14 Ч 3,032 = 28.843 м2, площадь апертуры зеркала;

при n=4

Построим график функции г`(Y0), по максимуму которого определим угол раскрыва зеркала.

График 1 – График функции г`(Y0)

Y0 = 0.945 (рад) = 54,145° Ю a1 = 0.931, g = 0.88, g` = 3,822 Ч10-4, g = 9,57 Ч10 –3.

Фокусное расстояние f может быть рассчитано на основе следующего соотношения:

В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении R0/f0 КНД наибольший. Заданный интервал отношения R0/f0 = (1,0…1,25). Расчетное отношение R0/f0 = 1,02, что удовлетворяет условию.

2 Расчет геометрических и электродинамических характеристик облучателей

Расчет сводиться к определению геометрических размеров облучателя, при которых уменьшение амплитуды поля на краю раскрыва зеркала происходит до одной трети амплитуды поля в центре раскрыва, и диаграммы направленности облучателя.

2.1 Полуволновый симметричный вибратор с контр рефлектором в виде диска

Фазовый центр вибратора с контр рефлектором в виде диска лежит между вибратором и контр рефлектором несколько ближе к последнему. Обычно контр рефлекторы выполняются в виде дисков диаметром 2d = (0.7…0.8)л, при этом ДН имеет форму, близкую к диаграмме с осевой симметрией, но, отличается от нее. Расстояние между вибратором и контр рефлектором выбирается близким к четверти длины волны, а длина вибратора – к половине длины волны (2l ≈ л/2).

Диаграмма направленности такого облучателя в Е плоскости рассчитывается по формуле:

а в Н плоскости – по формуле:

График 2 – ДН полуволнового симметричного вибратора с контр рефлектором в виде диска и аппроксимация.

2.2 распределение поля в апертуре зеркала

Расчет распределения поля в апертуре зеркала осуществляется по следующим формулам:

, где

График 3 – Распределение поля в апертуре зеркала

3 Расчет пространственной диаграммы направленности и определение параметров параболической антенны

Инженерный расчёт пространственной диаграммы направленности ДН параболической антенны часто сводится к определению ДН идеальной круглой синфазной площадки с неравномерным распределением напряжённости возбуждающего поля. В данном случае распределение напряжённости возбуждающего поля в основном определяется ДН облучателя в соответствующей плоскости. Выражение для нормированной ДН зеркальной параболической антенны при этом имеет вид:

где J1, J2 – цилиндрические функции Бесселя первого и второго порядка.

— коэффициент, показывающий во сколько раз амплитуда возбуждающего поля на краю раскрыва меньше амплитуды в центре раскрыва в соответствующей плоскости с учётом различий расстояний от облучателя до центра зеркала и до края зеркала;

Екр, Емах – амплитуды поля на краю и в центре раскрыва.

Для Е – плоскости к1 = 0.316

Для Н – плоскости к1 = 0.631

Построим ДН зеркальной параболической антенны:

График 4 – Пространственная ДН параболической антенны в Е плоскости.

График 5 – Пространственная ДН параболической антенны в Е плоскости.

Приближенно коэффициент направленного действия зеркальной антенны определяется выражением:

, где

S – площадь раскрыва;

хрез – результирующий коэффициент использования поверхности

Коэффициент использования поверхности:

Эффективная площадь антенны:

м2

Коэффициент направленного действия:

Коэффициент усиления антенны:

4 Конструктивный расчет антенны

4.1 Расчет профиля зеркала

Зеркальные антенны имеют наибольший КНД при синфазном возбуждении раскрыва (плоский фазовый фронт волны). Параболический профиль зеркала обеспечивает одинаковые длины электрических путей от облучателя, установленного в фокусе параболоида вращения, до каждой точки плоскости раскрыва (свойство параболы). В полярной системе координат парабола описывается уравнением

, где

Y изменяется от 0 до Y0.

График 6 – Плоский фазовый фронт волны

4.2 Выбор конструкции зеркала

С целью уменьшения веса и ветровых нагрузок поверхность зеркала часто выполняется перфорированной, или сетчатой

При такой конструкции зеркала часть энергии просачивается сквозь него, образуя нежелательное излучение. Допустимым является значение коэффициента прохождения в обратном направлении.

, где

Робр, Рпад – мощность излучения в обратном направлении и падающего на зеркало, соответственно.

Двухлинейная сетка работает удовлетворительно при расстоянии между проводниками меньше 0.1l и диаметре проводов не менее 0.01l.

dп = 0.1 Ч 0.273 = 0.027 м;

dпров = 0.01 Ч 0.273 = 0.0027 м.

4.3 Определение допусков на точность изготовления

Неточность изготовления зеркала вызывает несинфазность поля в раскрыве. Допустимыми являются фазовые искажения поля в раскрыве зеркала не более ± p/4. При этом уменьшение коэффициента усиления антенны не превышает нескольких процентов.

Пусть поверхность параболоида имеет некоторые неровности (выступы и углубления). Наибольшее отклонение от идеальной поверхности в направлении r обозначим через Дr.

Путь луча, отраженного от неровности в месте наибольшего отклонения от r, изменяется при этом на величину Dr + Dr Ч cosY, а соответствующий сдвиг фаз составит величину Dj = bЧDrЧ(1+cosY), и он не должен превышать величину p/4, отсюда получаем

Анализ полученного выражения для Dr показывает, что вблизи центра параболоида (Y = 0) необходимая точность изготовления зеркала наивысшая. Здесь наибольшее отклонение от идеальной поверхности не должно превосходить величины l/16, у кромки параболоида требования к точности получаются наименьшими.

Точность установки облучателя также определяется нормами на наибольшие допустимые фазовые искажения поля в раскрыве. Пусть фазовый центр облучателя смещен на Dх.

Тогда длины путей лучей от фазового центра до раскрыва увеличиваются. Наибольшее удлинение пути происходит у лучей, падающих на вершину зеркала. Это удлинение путей при малых смещениях можно приблизительно определить как DхcosY. Тогда изменение фазы составит величину

, где

Dj0, Djа – фазовые искажения, возникающие из-за неточности установки облучателя, в центре и на краю раскрыва, соответственно. Эта величина не должна превышать p/4, отсюда получаем: