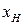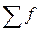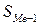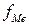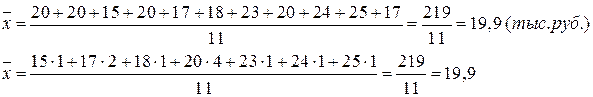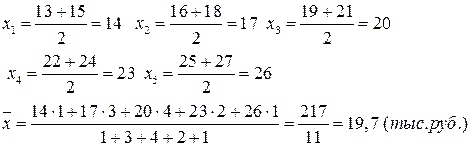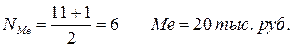Чем определяется однородность вариационного ряда
Вариационные ряды
| Главная > Учебные материалы > Математика: Вариационные ряды | ||
 | ||
 | ||
| 1.Вариационный ряд. 2.Числовые характеристики вариационного ряда. |
1.Вариационный ряд.
Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.

Таб.1
По данным таблицы построим полигон распределения частот (рис.1)
В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.

Таб. 2
По данным таблицы построим гистограмму распределения частот (рис.2)
Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.
2.Числовые характеристики вариационного ряда.
Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости.
Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической.
Дисперсией s 2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической.
Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии.
Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака.
Пример.
В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины.
Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен.
Как видно из таблицы сумма произведений x i n i = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда.

По данным таблицы построим гистограмму распределения частот.

Построим и эмпирическую функцию распределения случайной величины (кумуляту).


Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:
Дискретный вариационный ряд и его характеристики
п.1. Классификация рядов распределения
Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т.п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.
Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.
Распределение учеников по оценкам за контрольную работу
В данном ряду признак – это оценка, варианты признака \(x_i\) – это множество <2;3;4;5>, частоты \(f_i\) – это количество учеников, получивших каждую из оценок.
п.2. Дискретный вариационный ряд, полигон частот и кумулята
| Для распределения учеников по оценкам из нашего примера получаем такой полигон: |  |
Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(w_i\) | 0,0909 | 0,4545 | 0,3030 | 0,1515 | 1 |
| \(S_i\) | 0,0909 | 0,4545 | 0,8485 | 1 | — |
п.3. Выборочная средняя, мода и медиана
На полигоне частот мода – это абсцисса самой высокой точки.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
Например:
1) Найдем выборочную среднюю для распределения учеников по оценкам:
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(x_if_i\) | 6 | 45 | 40 | 25 | 116 |
п.4. Степень асимметрии вариационного ряда
В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».
Поэтому, кроме средней, в статистическом исследовании всегда следует определять моду и медиану.
Например:
Для распределения учеников по оценкам мы получили \(X_
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом \(\frac<|M_o-X_
п.5. Выборочная дисперсия и СКО
Например:
1) Найдем выборочную дисперсию для распределения учеников по оценкам:
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(x_i^2\) | 4 | 9 | 16 | 25 | — |
| \(x_i^2 f_i\) | 12 | 135 | 160 | 125 | 432 |
п.6. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
В теоретической статистике доказывается, что выборочная дисперсия D является смещенной оценкой дисперсии при распространении на генеральную совокупность.
А именно, выборочная дисперсия D всегда меньше математического ожидания для дисперсии генеральной совокупности.
Исправленная выборочная дисперсия S 2 является несмещенной оценкой.
Если показатель вариации V Внимание! Если исследуется не выборка, а вся генеральная совокупность, дисперсию «исправлять» не нужно.
п.7. Алгоритм исследования дискретного вариационного ряда
На входе: таблица с вариантами \(x_i\) и частотами \(f_i,\ i=\overline<1,k>\)
Шаг 1. Составить расчетную таблицу. Найти \(w_i,S_i,x_if_i,x_i^2,x_i^2f_i\)
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.8. Примеры
Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
В результате было получено следующее распределение:
| Число постоянных заказчиков | 0 | 1 | 2 | 3 | 4 | 5 |
| Число фрилансеров | 22 | 35 | 27 | 11 | 3 | 1 |
Исследуйте полученный вариационный ряд.
1) Вариационный ряд является дискретным.
Исследуемый признак – «число постоянных заказчиков».
Варианты признака \(x_i\in\left\<0;1;..;5\right\>\). Количество вариант k=6.
Составим расчетную таблицу:
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | ∑ |
| \(f_i\) | 23 | 35 | 27 | 11 | 3 | 1 | 100 |
| \(w_i\) | 0,23 | 0,35 | 0,27 | 0,11 | 0,03 | 0,01 | — |
| \(S_i\) | 0,23 | 0,58 | 0,85 | 0,96 | 0,99 | 1 | — |
| \(x_if_i\) | 0 | 35 | 54 | 33 | 12 | 5 | 139 |
| \(x_i^2\) | 0 | 1 | 4 | 9 | 16 | 25 | — |
| \(x_i^2f_i\) | 0 | 35 | 108 | 99 | 48 | 25 | 315 |
\(X_
При этом \(\frac<|M_0-X_
Основные характеристики вариационного ряда
Кубанский государственный университет
Кафедра экономического анализа, статистики и финансов
Методический материал
По дисциплине
«Теория статистики»
Составитель – к.э.н., доцент Бабенко И.В.
Краснодар 2016
ТЕМА 1 «Статистическое изучение вариационных рядов»
Общие сведения о вариационных рядах, их построение
Статистические ряды подразделяются на два вида: ряды распределения и ряды динамики.
Ряды распределения представляют собой ряды чисел, характеризующих состав или структуру какого-либо явления или процесса после группировки статистических данных. Ряды распределения подразделяются на атрибутивные и вариационные. Вариационные ряды, в свою очередь, могут быть дискретными и интервальными. В дискретном ряду группировочный признак изменяется прерывно, как правило, целыми числами.
В интервальном ряду группировочный признак принимает любые числовые значения в пределах интервала. Интервалы, в свою очередь, могут быть равновеликими и неравновеликими.
Вариационный ряд представляет собой две строки (или две колонки), в одной из которых приводятся отдельные значения варьирующего признака, которые называются вариантами и обозначаются символом x, а в другой строке – абсолютные числа, показывающие, сколько раз встречается тот или иной вариант. Эти показатели второй строки (колонки) называются частотами и обозначаются обычно через m(f).
Во второй строке могут использоваться и относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот. Их именуют частостями и обозначают w 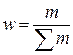
Пример атрибутивного ряда:
Крупнейшие производители мобильных телефонов в 2012 г., доля на мировом рынке в процентах
| Samsung | Nokia | Apple | ZTE | LG | Прочие | Итого |
| 23,7 | 19,6 | 8,0 | 3,8 | 3,3 | 41,6 |
Ежедневный товарооборот, тыс. руб. (Величина уплаченных штрафов)
20 20 15 20 17 18 23 20 24 25 17
Дискретный вариационный ряд:
| x | Итого | ||||||
| m | |||||||
| S | 1+2=3 | 3+1=4 | 4+4=8 | 8+1=9 | 9+1=10 | 10+1=11 | – |
Интервальный вариационный ряд (равновеликий):
| x | 13-15 | 16-18 | 19-21 | 22-24 | свыше 24 | Итого |
| m | ||||||
| w | 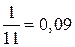 (9%) (9%) | 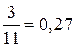 (27%) (27%) | 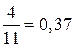 (37%) (37%) | 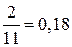 (18%) (18%) | 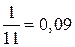 (9%) (9%) | 1,00 (100%) |
Для целых чисел признака границы интервалов могут не пересекаться, а для дробных – пересекаются во всех случаях.
Основные характеристики вариационного ряда
Средняя арифметическая. Для несгруппированных данных средняя арифметическая рассчитывается по формуле:
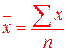
и называется средней арифметической простой.
Для дискретного вариационного ряда (где данные уже сгруппированы) рассчитывается средняя арифметическая взвешенная:
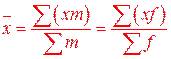
Понятие «вес» не всегда связано с подсчётом частот вариантов, и, следовательно, с вариационными рядами.
Для интервального вариационного ряда для исчисления 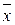
Важнейшее свойство средней арифметической: сумма отклонений вариантов от своей средней арифметической равна нулю
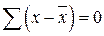
Средняя гармоническая.
Средняя гармоническая простая 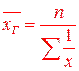
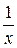
Средняя гармоническая взвешенная 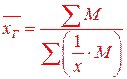
Применение средней арифметической или средней гармонической определяется наличием данных и исходным статистическим соотношением (ИСС).
Кроме вышеуказанных средних, рассчитываются и структурные средние:
Мода (Мо) – это наиболее часто встречающееся значение признака у единиц совокупности. Для дискретных рядов – это вариант, имеющий наибольшую частоту (для наших данных Мо=20 тыс. руб.).
В интервальных вариационных рядах вначале по наибольшей частоте определяют интервал, в котором находится мода – модальный интервал. Для рядов с равными интервалами мода определяется по следующей формуле:
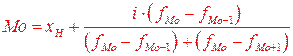
где 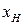
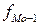
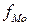
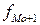
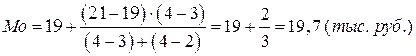
В ряду с неравными интервалами Мо определяется в интервале, имеющем наибольшую плотность распределения, и в формуле вместо частот принимаются соответствующие плотности распределения. Плотность распределения рассчитывается делением количества единиц в интервале на величину интервала.
Медиана (Ме) – это значение признака у средней единицы ранжированного ряда. Ранжированным называется ряд, у которого значения признака расположены в порядке возрастания или убывания.
Для нахождения медианы в случае несгруппированных данных вначале определяют её порядковый номер: 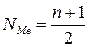
| №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |
Для определения медианы в дискретном ряду также находят её порядковый номер: 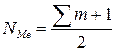
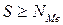
| x | Итого | ||||||
| m | |||||||
| S | 1+2=3 | 1+2+1=4 | 1+2+1+4=8 | 1+2+1+4+1=9 | 1+2+1+4+1+1=10 | 1+2+1+4+1+1+1=11 | – |
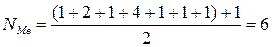
В интервальном ряду, прежде всего, находят медианный интервал; им считается тот, накопленная частота которого впервые больше или равна половины всей суммы частот 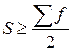
Медиана в этом случае находится по формуле:
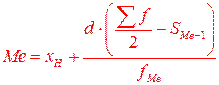
где