Чем определяется объем знаний человека получающего сообщение

Чем определяется объем знаний человека получающего сообщение

В содержательном подходе количество информации, заключенное в сообщении, определяется объемом знаний, который это сообщение несет получающему его человеку.

Процесс познания можно изобразить в виде расширяющегося “круга знания“, всё что за пределами круга – область незнания.

И вот здесь как раз проявляется парадокс:

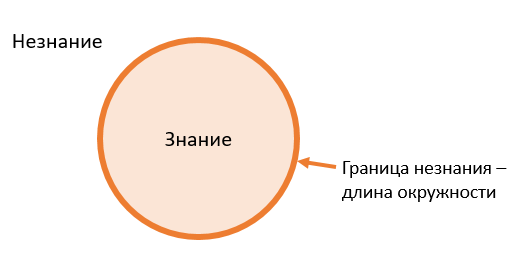
Чем больше знаешь, тем больше понимаешь, что ничего не знаешь…

Другими словами, по мере получения знаний, человек раздвигает границы познания, но при этом всё больше осознает объёмы своего незнания.

Например, знания выпускника школы гораздо больше чем знания первоклассника, но и граница его незнания также существенно больше, т.е. старшеклассник при подготовке к выпускным экзаменам обнаруживает непонимание некоторых законов или правил и вынужден их восполнять. Тогда как первоклассник вообще ничего не знает об этих законах и правилах.

Подход к измерению информации, как способу уменьшения неопределённости знания, позволяет измерять информацию, особенно это ВАЖНО для информатики, которая изучает процессы хранения и передачи информации.

Информацию можно рассматривать как набор сообщений.

Сообщение – это форма представления каких-либо сведений в виде речи, текста, изображений, графиков, таблиц и т.д.

Информация – это знания, которые мы получаем из внешнего мира. Количество информации, заключенное в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.

1 бит – минимальная единица измерения количества информации.

Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.

Допустим, вы бросаете, загадывая, что выпадет: орел или решка.

Есть всего два возможных результата бросания монеты. Причем ни один из этих результатов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.

В случае с монетой перед ее подбрасыванием неопределенность знания о результате равна двум.

Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знания о результате бросания кубика равна шести.

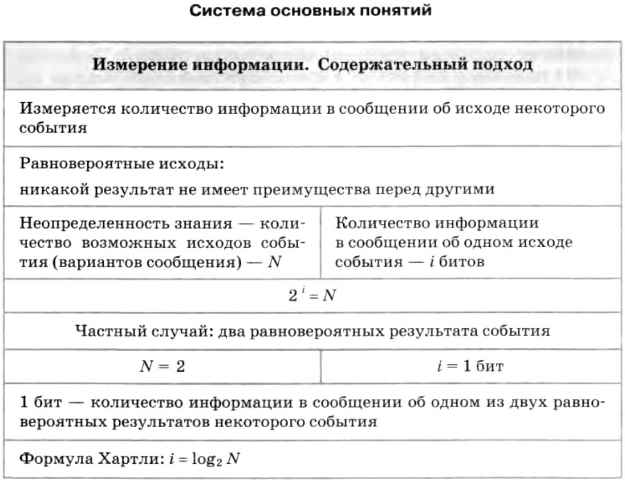
Неопределенность знания о результате некоторого события (бросание монеты или игрального кубика, жребий и др.) – это количество возможных результатов.

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий.

Тогда количество информации i, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, можно определить из формулы Хартли:

Шахматная доска состоит из 64 полей: 8 столбцов на 8 строк.

Какое количество бит несет сообщение о выборе одного шахматного поля?

Поскольку выбор любой из 64 клеток равновероятен, то количество бит находится из формулы:

Источник

Чем определяется объем знаний человека получающего сообщение

Урок 6. Содержательный (вероятностный) подход к измерению информации

Измерение информации. Содержательный подход

Неопределенность знания и количество информации

Содержательный подход к измерению информации отталкивается от определения информации как содержания сообщения, получаемого человеком. Сущность содержательного подхода заключается в следующем: сообщение, информирующее об исходе какого-то события, снимает неопределенность знания человека об этом событии.

Чем больше первоначальная неопределенность знания, тем больше информации несет сообщение, снимающее эту неопределенность.

Приведем примеры, иллюстрирующие данное утверждение.

Ситуация 1. В ваш класс назначен новый учитель информатики; на вопрос «Это мужчина или женщина?» вам ответили: «Мужчина».

Ситуация 2. На чемпионате страны по футболу играли команды «Динамо» и «Зенит». Из спортивных новостей по радио вы узнаете, что игра закончилась победой «Зенита».

Ситуация 3. На выборах мэра города было представлено четыре кандидата. После подведения итогов голосования вы узнали, что избран Н. Н. Никитин.

Вопрос: в какой из трех ситуаций полученное сообщение несет больше информации?

Неопределенность знания — это количество возможных вариантов ответа на интересовавший вас вопрос. Еще можно сказать: возможных исходов события. Здесь событие — например, выборы мэра; исход — выбор, например, Н. Н. Никитина.

В первой ситуации 2 варианта ответа: мужчина, женщина; во второй ситуации 3 варианта: выиграл «Зенит», ничья, выиграло «Динамо»; в третьей ситуации — 4 варианта: 4 кандидата на пост мэра.

Согласно данному выше определению, наибольшее количество информации несет сообщение в третьей ситуации, поскольку неопределенность знания об исходе события в этом случае была наибольшей.

В 40-х годах XX века проблема измерения информации была решена американским ученым Клодом Шенноном — основателем теории информации. Согласно Шеннону, информация — это снятая неопределенность знания человека об исходе какого-то события.

В теории информации единица измерения информации определяется следующим образом.

Сообщение, уменьшающее неопределенность знания об исходе некоторого события в два раза, несет 1 бит информации.

Согласно этому определению, сообщение в первой из описанных ситуаций несет 1 бит информации, поскольку из двух возможных вариантов ответа был выбран один.

Следовательно, количество информации, полученное во второй и в третьей ситуациях, больше, чем один бит. Но как измерить это количество?

Рассмотрим еще один пример.

Ученик написал контрольную по информатике и спрашивает учителя о полученной оценке. Оценка может оказаться любой: от 2 до 5. На что учитель отвечает: «Угадай оценку за два вопроса, ответом на которые может быть только «да» или «нет»». Подумав, ученик задал первый вопрос: «Оценка выше тройки?». «Да», — ответил учитель. Второй вопрос: «Это пятерка?». «Нет», — ответил учитель. Ученик понял, что он получил четверку. Какая бы ни была оценка, таким способом она будет угадана!

Первоначально неопределенность знания (количество возможных оценок) была равна четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.

Узнав оценку (одну из четырех возможных), ученик получил 2 бита информации.

Рассмотрим еще один частный пример, а затем выведем общее правило.

Вы едете на электропоезде, в котором 8 вагонов, а на вокзале вас встречает товарищ. Товарищ позвонил вам по мобильному телефону и спросил, в каком вагоне вы едете. Вы предлагаете угадать номер вагона, задав наименьшее количество вопросов, ответами на которые могут быть только слова «да» или «нет».

Немного подумав, товарищ стал спрашивать:

Схематически поиск номера вагона выглядит так:

Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, в сумме набрано 3 бита информации. То есть сообщение о том, что вы едете в пятом вагоне, несет 3 бита информации.

Способ решения проблемы, примененный в примерах с оценками и вагонами, называется методом половинного деления: ответ на каждый вопрос уменьшает неопределенность знания, имеющуюся перед ответом на этот вопрос, наполовину. Каждый такой ответ несет 1 бит информации.

Заметим, что решение подобных проблем методом половинного деления наиболее рационально. Таким способом всегда можно угадать, например, любой из восьми вариантов за 3 вопроса. Если бы поиск производился последовательным перебором: «Ты едешь в первом вагоне?» «Нет», «Во втором вагоне?» «Нет» и т. д., то про пятый вагон вы смогли бы узнать после пяти вопросов, а про восьмой — после восьми.

«Главная формула» информатики

Сформулируем одно очень важное условие, относящееся к рассмотренным примерам. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Равновероятно, что учитель может быть мужчиной или женщиной; равновероятен любой исход футбольного матча, равновероятен выбор одного из четырех кандидатов в мэры города. То же относится и к примерам с оценками и вагонами.

Тогда полученные нами результаты описываются следующими формулировками:

• сообщение об одном из двух равновероятных исходов некоторого события несет 1 бит информации;
• сообщение об одном из четырех равновероятных исходов некоторого события несет 2 бита информации;
• сообщение об одном из восьми равновероятных исходов некоторого события несет 3 бита информации.

Обозначим буквой N количество возможных исходов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из N результатов.

Нетрудно заметить, что связь между этими величинами выражается следующей формулой:

2 i = N.

Действительно: 2 1 = 2 ; 2 2 = 4 ; 2 3 = 8.

С полученной формулой вы уже знакомы из курса информатики для 7 класса и еще не однажды с ней встретитесь. Значение этой формулы столь велико, что мы назвали ее главной формулой информатики. Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике такое уравнение называется показательным уравнением.

Пример. Вернемся к рассмотренному выше примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Чтобы ответить на вопрос, какое количество информации содержится в сообщении о номере искомого вагона, нужно решить уравнение:

2 i = 16.

Количество информации i, содержащееся в сообщении об одном из N равновероятных исходов некоторого события, определяется из решения показательного уравнения:

2 i = N.

Пример. В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несет сообщение о том, что вам купили билет на 12-й ряд, 10-е место?

Но эту же задачу можно решать иначе. Сообщение о номере ряда несет 4 бита информации, так как 2 4 = 16. Сообщение о номере места несет 5 битов информации, так как 2 5 = 32. В целом сообщение про ряд и место несет: 4 + 5 = 9 битов информации.

Данный пример иллюстрирует выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.

Сделаем одно важное замечание. С формулой 2 i = N мы уже встречались, обсуждая алфавитный подход к измерению информации (см. § 3. Измерение информации. Алфавитный подход). В этом случае N рассматривалось как мощность алфавита, а i — как информационный вес каждого символа алфавита. Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, т. е. равновероятно, то информационный вес символа i тождественен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределенность знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Данный факт демонстрирует связь между алфавитным и содержательным подходами к измерению информации.

Формула Хартли

Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»-«Зенит»? В этой ситуации N = 3. Можно догадаться, что решение уравнения

2 i = 3.

будет дробным числом, лежащим между 1 и 2, поскольку 2 1 = 2 2 = 4 > 3. А как точнее узнать это число?

В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:

Читается это так: «логарифм от N по основанию 2». Смысл очень простой: логарифм по основанию 2 от А — это степень, в которую нужно возвести 2, чтобы получить N. Например, вычисление уже известных вам значений можно представить так:

Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 1.4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.

В табличном процессоре Microsoft Excel функция логарифма имеет следующий вид: LOG(apryмент; основание). Аргумент — значение N находится в ячейке А2, а основание логарифма равно 2. В результате получаем с точностью до девяти знаков после запятой: i = log₂3 = 1,584962501 (бита).

Формула для измерения количества информации: i = log₂N была предложена американским ученым Ральфом Хартли — одним из основоположников теории информации.

Формула Хартли: i = log₂ N
Здесь i — количество информации, содержащееся в сообщении об одном из N равновероятных исходов события.

Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, в то время как информационный объем, вычисляемый путем применения алфавитного подхода, может иметь только целочисленное значение.

Вопросы и задания

1. Что такое неопределенность знания об исходе некоторого события?
2. Как определяется единица измерения количества информации в рамках содержательного подхода?
3. Придумайте несколько ситуаций, при которых сообщение несет 1 бит информации.
4. В каких случаях и по какой формуле можно вычислить количество информации, содержащейся в сообщении, используя содержательный подход?
5. Сколько битов информации несет сообщение о том, что из колоды в 32 карты достали «даму пик»?
6. При угадывании методом половинного деления целого числа из диапазона от 1 до N был получен 1 байт информации. Чему равно N?
7. Проводятся две лотереи: «4 из 32» и «5 из 64». Сообщение о результатах какой из лотерей несет больше информации?
8. Используя формулу Хартли и электронные таблицы, определите количество информации в сообщениях о равновероятных событиях:
а) на шестигранном игральном кубике выпала цифра 3;
б) в следующем году ремонт в школе начнется в феврале;
в) я приобрел абонемент в бассейн на среду;
г) из 30 учеников класса дежурить в школьной столовой назначили Дениса Скворцова.
9. Используя закон аддитивности количества информации, решите задачу о билете в кинотеатр со следующим дополнительным условием: в кинотеатре 4 зала. В билете указан номер зала, номер ряда и номер места. Какое количество информации заключено в билете?

Источник

Чем определяется количество информации в сообщении

Процесс познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и т. д.). Получение новой информации приводит к расширению знаний или, как иногда говорят, к уменьшению неопределенности знания. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.

Например, после сдачи зачета или выполнения контрольной работы вы мучаетесь неопределенностью, вы не знаете, какую оценку получили. Наконец, учитель объявляет результаты, и вы получаете одно из двух информационных сообщений: «зачет» или «незачет», а после контрольной работы одно из четырех информационных сообщений: «2», «3», «4» или «5».

Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности вашего знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности вашего знания в четыре раза, так как получено одно из четырех возможных информационных сообщений.

Ясно, что чем более неопределенна первоначальная ситуация (чем большее количество информационных сообщений возможно), тем больше мы получим новой информации при получении информационного сообщения (тем в большее количество раз уменьшится неопределенность знания).

Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.

Рассмотренный выше подход к информации как мере уменьшения неопределенности знания позволяет количественно измерять информацию. Существует формула, которая связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение:

Бит. Для количественного выражения любой величины необходимо сначала определить единицу измерения. Так, для измерения длины в качестве единицы выбран метр, для измерения массы – килограмм и т. д. Аналогично, для определения количества информации необходимо ввести единицу измерения.

За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа битом.

Если вернуться к рассмотренному выше получению информационного сообщения о результатах зачета, то здесь неопределенность как раз уменьшается в два раза и, следовательно, количество информации, которое несет сообщение, равно 1 биту.

Производные единицы измерения количества информации. Минимальной единицей измерения количества информации является бит, а следующей по величине единицей – байт, причем:

1 байт = 8 битов = 2 3 битов.

В компьютере информация кодируется с помощью двоичной знаковой системы, и поэтому в кратных единицах измерения количества информации используется коэффициент 2 n

Так, кратные байту единицы измерения количества информации вводятся следующим образом:

1 килобайт (Кбайт) = 2 10 байт = 1024 байт;

1 мегабайт (Мбайт) = 2 10 Кбайт = 1024 Кбайт;

1 гигабайт (Гбайт) = 2 10 Мбайт = 1024 Мбайт.

1. Приведите примеры информационных сообщений, которые приводят к уменьшению неопределенности знания.
2. Приведите примеры информационных сообщений, которые несут 1 бит информации.

Определение количества информационных сообщений.По формуле (1.1) можно легко определить количество возможных информационных сообщений, если известно количество информации. Например, на экзамене вы берете экзаменационный билет, и учитель сообщает, что зрительное информационное сообщение о его номере несет 5 битов информации. Если вы хотите определить количество экзаменационных билетов, то достаточно определить количество возможных информационных сообщений об их номерах по формуле (1.1):

Таким образом, количество экзаменационных билетов равно 32.

Определение количества информации. Наоборот, если известно возможное количество информационных сообщений N, то для определения количества информации, которое несет сообщение, необходимо решить уравнение относительно I.

Представьте себе, что вы управляете движением робота и можете задавать направление его движения с помощью информационных сообщений: «север», «северо-восток», «восток», «юго-восток», «юг», «юго-запад», «запад» и «северо-запад» (рис. 1.11). Какое количество информации будет получать робот после каждого сообщения?

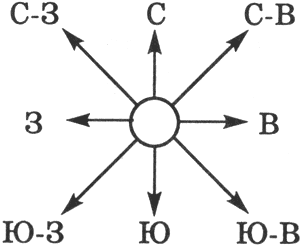Рис. 1.4. Управление роботом с использованием информационных сообщений

Всего возможных информационных сообщений 8, поэтому формула (1.1) принимает вид уравнения относительно I:

Разложим стоящее в левой части уравнения число 8 на сомножители и представим его в степенной форме:

Равенство левой и правой частей уравнения справедливо, если равны показатели степени числа 2. Таким образом, I = 3 бита, т. е. количество информации, которое несет роботу каждое информационное сообщение, равно 3 битам.

Алфавитный подход к определению количества информации

При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.

Рис. 1.5. Передача информации

Формула (1.1) связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение. Тогда в рассматриваемой ситуации N – это количество знаков в алфавите знаковой системы, а I – количество информации, которое несет каждый знак:

С помощью этой формулы можно, например, определить количество информации, которое несет знак в двоичной знаковой системе:

Таким образом, в двоичной знаковой системе знак несет 1 бит информации. Интересно, что сама единица измерения количества информации «бит» (bit) получила свое название ОТ английского словосочетания «Binary digiT» – «двоичная цифра».

Информационная емкость знака двоичной знаковой системы составляет 1 бит.

Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. В качестве примера определим количество информации, которое несет буква русского алфавита. В русский алфавит входят 33 буквы, однако на практике часто для передачи сообщений используются только 32 буквы (исключается буква «ё»).

С помощью формулы (1.1) определим количество информации, которое несет буква русского алфавита:

Таким образом, буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению количества информации).

Количество информации, которое несет знак, зависит от вероятности его получения. Если получатель заранее точно знает, какой знак придет, то полученное количество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его информационная емкость.

В русской письменной речи частота использования букв в тексте различна, так в среднем на 1000 знаков осмысленного текста приходится 200 букв «а» и в сто раз меньшее количество буквы «ф» (всего 2). Таким образом, с точки зрения теории информации, информационная емкость знаков русского алфавита различна (у буквы «а» она наименьшая, а у буквы «ф» – наибольшая).

Количество информации в сообщении. Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.

Если знаки несут одинаковое количество информации, то количество информации I_c в сообщении можно подсчитать, умножив количество информации I_з, которое несет один знак, на длину кода (количество знаков в сообщении) К:

Так, каждая цифра двоичного компьютерного кода несет информацию в 1 бит. Следовательно, две цифры несут информацию в 2 бита, три цифры – в 3 бита и т. д. Количество информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.1).

Все мы привыкли к тому, что все вокруг можно измерить. Мы можем определить массу посылки, длину стола, скорость движения автомобиля. Но как определить количество информации, содержащееся в сообщении? Ответ на вопрос в статье.

Итак, давайте для начала выберем сообщение. Пусть это будет «Принтер — устройство вывода информации.«. Наша задача — определить, сколько информации содержится в данном сообщении. Иными словами — сколько памяти потребуется для его хранения.

Определение количества информации в сообщении

Для решения задачи нам нужно определить, сколько информации несет один символ сообщения, а потом умножить это значение на количество символов. И если количество символов мы можем посчитать, то вес символа нужно вычислить. Для этого посчитаем количество различных символов в сообщении. Напомню, что знаки препинания, пробел — это тоже символы. Кроме того, если в сообщении встречается одна и та же строчная и прописная буква — мы считаем их как два различных символа. Приступим.

В слове Принтер 6 различных символов (р встречается дважды и считается один раз), далее 7-й символ пробел и девятый — тире. Так как пробел уже был, то после тире мы его не считаем. В слове устройство 10 символов, но различных — 7, так как буквы с, т и о повторяются. Кроме того буквы т и р уже была в слове Принтер. Так что получается, что в слове устройство 5 различных символов. Считая таким образом дальше мы получим, что в сообщении 20 различных символов.

Далее вспомним формулу, которую называют главной формулой информатики:

Подставив в нее вместо N количество различных символов, мы узнаем, сколько информации несет один символ в битах. В нашем случае формула будет выглядеть так:

Вспомним степени двойки и поймем, что i находится в диапазоне от 4 до 5 (так как 2 4 =16, а 2 5 =32). А так как бит — минимальная единица измерения информации и дробным быть не может, то мы округляем i в большую сторону до 5. Иначе, если принять, что i=4, мы смогли бы закодировать только 2 4 =16 символов, а у нас их 20. Поэтому получаем, что i=5, то есть каждый символ в нашем сообщении несет 5 бит информации.

Осталось посчитать сколько символов в нашем сообщении. Но теперь мы будем считать все символы, не важно повторяются они или нет. Получим, что сообщение состоит из 39 символов. А так как каждый символ — это 5 бит информации, то, умножив 5 на 39 мы получим:

5 бит x 39 символов = 195 бит

Это и есть ответ на вопрос задачи — в сообщении 195 бит информации. И, подводя итог, можно написать алгоритм нахождения объема информации в сообщении:

Объемный способ измерения информации

Технический способ измерения количества информации (или, точнее, информационного объема сообщения) основан на подсчета количества символов, из которых образовано сообщение. При этом не учитывается смысловое содержание сообщения. Например, многократное повторение одного и того же текста не несет новой информации, однако в результате занимает больший объем памяти, требует большего времени для передачи и т.п. Поэтому этот способ удобен в технических расчетах.

Американский математик и инженер К. Шеннон в 1948 г. получил формулу для расчета количества информации, содержащейся в системе, обладающей произвольным набором неравновероятных (в общем случае) состояний

где n – число возможных состояний системы, pi – вероятность i-го состояния (причем pi = 1)

Чем меньше вероятность наступления события, тем большую информацию это событие несет.

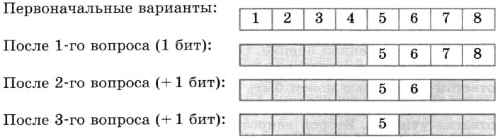
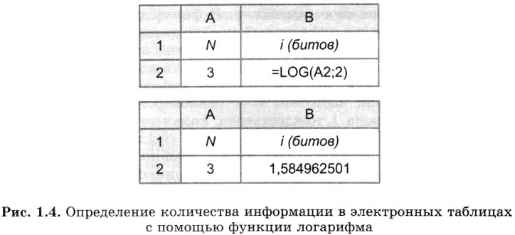
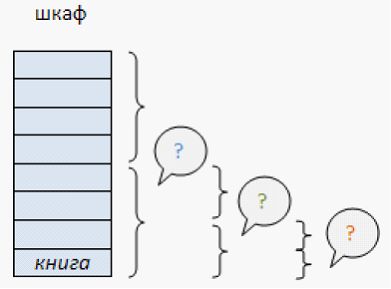
На книжном стеллаже восемь полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга?

Применим метод половинного деления. Зададим несколько вопросов уменьшающих неопределенность знаний в два раза.

– Книга лежит выше четвертой полки?

Книга — на второй полке?

Ну теперь все ясно! Книга лежит на первой полке! Каждый ответ уменьшал неопределенность в два раза.

Всего было задано три вопроса. Значит набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.

Если обозначить возможное количество событий, или, другими словами, неопределенность знаний N, а буквой I количество информации в сообщении о том, что произошло одно из N событий, то можно записать формулу:

Количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется из решения показательного уравнения:

А теперь познакомимся с другим способом измерения информации. Этот способ не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом.

При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.

Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.

Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54.

В каждой очередной позиции текста может появиться любой из N символов. Тогда, согласно известной нам формуле, каждый такой символ несет I бит информации, которое можно определить из решения уравнения: 2I = 54. Получаем: I = 5.755 бит.

Вот сколько информации несет один символ в русском тексте! А теперь для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на I.

Посчитаем количество информации на одной странице книги. Пусть страница содержит 50 строк. В каждой строке — 60 символов. Значит, на странице умещается 50×60=3000 знаков. Тогда объем информации будет равен: 5,755 х 3000 = 17265 бит.

При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.

Пусть небольшая книжка, сделанная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов. Значит страница содержит 40×60=2400 байт информации. Объем всей информации в книге: 2400 х 150 = 360 000 байт.

В любой системе единиц измерения существуют основные единицы и производные от них.

Для измерения больших объемов информации используются следующие производные от байта единицы:

1 килобайт = 1Кб = 210 байт = 1024 байта.

1 мегабайт = 1Мб = 210 Кб = 1024 Кб.

1 гигабайт = 1Гб = 210 Мб = 1024 Мб.

Прием-передача информации могут происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации или скорость информационного потока.

Очевидно, эта скорость выражается в таких единицах, как бит в секунду (бит/с), байт в секунду (байт/с), килобайт в секунду (Кбайт/с) и т.д.

Вопросы для самопроверки

Вопросы для самопроверки

1. Формальная и неформальная постановка задачи.

2. Дайте определение «модель» и требования к моделированию.

3. Характеристика стадий построения информационной модели.

4. Классификация моделей.

5. Виды форм представления информационных моделей.

6. Этапы разработки компьютерных моделей.

7. Информация, классификация информации.

8. Методы получения и использования информации.

9. Носитель информации.

10. Способы измерения информации.

11. Алфавитный подход к измерения информации.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8956 – | 7623 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Источник