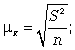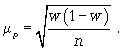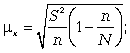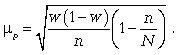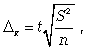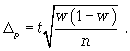Чем определяется объем выборки исследования

Объем выборки: понятие и способы расчета. Этапы и процедуры работы с выборкой

Этапы и процедуры работы с выборкой.

Этапы: 1)подготовительный-определяется объект исследования генеральной совокупности, ее границы и размеры собирательно-статистической информации о генеральной совокупности( если онаимеется), формируется предварительная модель генеральной совокупности. 2)проектирование-проверка выборки, объем выборки, тип выборки, определяется единица отбора и единица наблюдения, выбирается их метод отбора, определяется наличие ступеней, выбирается основа выборки, отбирается тип опроса, осуществляются необходимые расчеты, делается предварительная оценка выборки на репрезентативность, составляется инструкция по отбору респондентов. 3)реализация-формирование выборки(полевой этап) респондентов отбирают согласно выбранному методу выборки, отбор единиц наблюдения по инструкции, замена недостижимых респондентов при необходимости, контроль интервьюеров по выбранным респондентам, предварительное оценивание формирования выборки.

4)заключительный-оценивание сформировавшейся выборки на соответствие проекту, выявляется отклонение по социально-демографическим характеристикам, ремонт выборки(при необходимости).

Объем выборки: понятие и способы расчета.

Объем выборки – это количество единиц попавших в выборочную совокупность.

При определении объема выборки нужно прежде решить задачу требуемого исследователю уровня точности результата (Д), гарантируемого с некоторой заранее заданной доверитель­ной вероятностью (Р).Существуют три стратегии расчета объема выборки.1. Стратегия предварительного расчета(до проведения исследования). Это лишь первоначальный ориентир, так как, не принимается во внимание из-за неопределенности разброс мне­ний; а поэтому исходят из соотношения 50:50% (половина отве­тов «да», половина «нет»).2. Стратегия последовательного расчета выборки.Ис­пользуется, когда каждое интервью очень дорогостоящее или слишком длительное. Тогда объем выборки не рассчитывается заранее, а ставится в зависимость от результатов, полученных входе исследования. Например, сначала опрашивается 100 чело­ век, на основе полученных данных о разбросе оценки вычисля­ют требуемый объем. Если оказывается, что этого количества
опрошенных достаточно, то исследование прекращается. В про­тивном случае добирают необходимое количество респонден­тов.3. Стратегия комбинированного расчета.Рассчитывая вы­борку по предварительной стратегии, получаем верхние преде­лы допустимых объемов выборки, то есть ту величину выборки, при достижении которой прекращается опрос по последователь­ной стратегии.На практике существуют удобные способы определения объемов выборки с помощью таблицы больших чисел и с помощью номограммы для определения объема выборки.На величину объема выборки также влияет типичный объем выборок, используемых в аналогичных исследованиях.

Для проведения социологического исследования недостаточно просто определить объект исследования. Нерационально опрашивать всех людей, составляющих объект исследования (иногда это могут быть тысячи людей). Обычно СИ имеют не сплошной, а выборочный характер. То есть по определенным и строгим правилам исследователь отбирает небольшое (относительно всего объема выборки) число людей, которые по своим социально-демографическим признакам и другим каким-то характеристикам полностью соответствуют структуре изучаемого объекта.

Источник

Определение объема выборки

Решение об объеме выборки является компромиссом между теоретическими предположениями о точности результатов обследования и возможностями их практической реализации. Известно, что чем больше объем выборки, тем меньше ее ошибка. Однако необходимо учитывать, что, стоимость выборки растет пропорционально ее объему, а ошибка выборки уменьшается по норме, равной квадратному корню из относительного роста размера выборки. Если размер выборки увеличить в 4 раза, то ошибка выборки уменьшится только на половину.

Оптимальный объём выборки зависит от следующих параметров:

— изучаемых характеристик и их распределения в генеральной совокупности;

— доступных ресурсов (финансовых, временных) для исследования.

Подходы к определению объема выборки.

Произвольный подход основан на применении «правила большого пальца». Например, бездоказательно принимается, что для получения точных результатов выборка должна составлять 5% от генеральной совокупности.

Объем выборки может быть установлен исходя из некоторых заранее оговоренных условий. При изучении общественного мнения выборка обычно составляет 1000-1200 человек.

В случае, если на каком-то рынке проводятся ежегодные исследования, то в каждом году используется выборка одного и того же объема.

Объем выборки может определяться на основе статистического анализа. Этот подход основан на определении минимального объема выборки исходя из требований к надежности и достоверности получаемых результатов.

В математической теории выборочного наблюдения доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Принципиальную возможность определения генеральной средней по данным простой случайной выборки доказывает теорема П.Л. Чебышева, также известная как «закон больших чисел». В приложении к выборочному методу неравенство. П.Л. Чебышева может быть сформулировано так: при неограниченном, увеличении числа независимых наблюдений в генеральной совокупности с ограниченной дисперсией с вероятностью, сколь угодно близкой к единице, можно ожидать, что отклонение выборочной средней от генеральной средней будет сколь угодно мало.

Центральная предельная теорема А. М. Ляпунова, доказана в 1901 г. Согласно этой теореме, при достаточно большом числе независимых наблюдений и генеральной совокупности с конечной средней и ограниченной дисперсией вероятность того, что расхождение между выборочной и генеральной средней \х

-х\ не превзойдет по абсолютной величине, некоторую величину, равна интегралу Лапласа.

Нормальное распределение на графике выглядит как непрерывная кривая. Площадь, ограниченная этой кривой над любым заданным отрезком оси х, равна частоте или вероятности попадания случайного числа на этот отрезок.

Среднее арифметическое находится при помощи усреднения, т.е. сложения данных и деления полученного результата на количество слагаемых.

Понятие вариации характеризует величину несхожести (схожести) ответов респондентов на определенный вопрос. В качестве меры вариации обычно принимается среднее квадратическое отклонение, которое характеризует среднее расстояние от средней оценки ответов каждого респондента на определенный вопрос.

При определении объёма выборки исследователь использует два основных статистических параметра: точность оценки и степень достоверности оценки.

Точность оценки – величина ошибки результата в абсолютном или относительном выражении. Степень достоверности оценки – вероятность того, что оценка соответствует истинному значению при установленной точности, т.е. вероятность гарантирующая результат.

Доверительный интервал – интервал, в который попадает определенный процент выборочных средних.

Из свойств нормальной кривой распределения вытекает, что конечные точки доверительного интервала, равного скажем 95%, определяются как произведение 1,96, называемого нормированным отклонением, на среднее квадратическое отклонение. Числа 1,96 и 2,58 (для 99%-ного доверительного интервала) обозначаются как z. Имеются таблицы «Значения интеграла вероятностей», которые дают возможность определить величины z для различных доверительных интервалов. Доверительный интервал, равный или 95%, или 99%, является стандартным при проведении маркетинговых исследований.

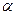
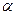Значение нормированного отклонения оценки (z) от среднего значения в зависимости от доверительной вероятности () полученного результата.

, %	99,7
z	0,84	1,03	1,29	1,44	1,65	1,96	2,18	2,58	3,0

В общем случае, для выборок достаточно большого объёма (больше 30 элементов) при оценке уровня среднего значения признака в генеральной совокупности, объём определяется по следующей формуле:

z – нормированное отклонение, соответствующее принятому уровню доверительной вероятности (то есть вероятности, с которой истинное значение признака в генеральной совокупности будет соответствовать значению признака в выборочной совокупности), определяется по статистическим таблицам;

e 2 – предельная ошибка выборки (то есть величина, устанавливающая границы интервала относительно выборочного среднего значения, в которые с указанной доверительной вероятностью попадёт генеральное среднее значение изучаемого признака);

N – объем генеральной совокупности

Величина σ² зачастую бывает неизвестна, поэтому используют приближенные способы ее оценки:

Возможно определение объема выборки на основе процентных величин. Например, исследуется мнение потребителей о новом продукте и заказчик данного исследования указал, что его устроит точность полученных результатов, равная 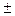5%. Предположим, что 30% членов выборки высказалось за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25% – 35%. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.

Когда на исходный вопрос существует только два варианта ответа, выраженное в % (например, 30% респондентов будет покупать новый продукт, а 70% не будет покупать новый продукт), объем выборки определяется по следующей формуле:

,

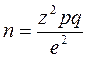
где n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности;

р – найденная вариация для выборки;

e – допустимая ошибка.

При использовании процентной меры изменчивости принимается в расчет то обстоятельство, что максимальная изменчивость достигается для p = 50%, что является наихудшим случаем. Иногда, когда невозможно определить вариацию для выборки используют максимальную меру изменчивости.

Приведенные формулы расчета объема выборки основаны на предположении, что все правила формирования выборки были соблюдены и единственной ошибкой выборки является ошибка, обусловленная ее объемом. Однако, следует помнить, что объем выборки определяет точность полученных результатов, но не их представительность, которая определяется методом формирования выборки.

1. В ходе исследования запланировано выяснить отношение жителей города Воронежа к новому продукту – соль диетическая. Предварительные данные отсутствуют. Необходимо определить объем выборки для поквартирного опроса методом личного интервью. Заказчика устроит уровень доверительной вероятности, равный 95%, если ошибка будет составлять не более 3%.

Применим формулу:

,

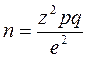
где n – размер выборки;

Получаем: n = 1067.

2. Количество предприятий, использующих в своем производстве конвейерную ленту общего назначения, составляет 2300. Доля предприятий, предпочитающих импортную ленту, по предварительным данным составляет около 20%. При величине доверительной вероятности 95% найти объем выборки, если ошибка должна составить не более 5%.

Применим формулу:

,

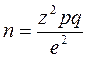
где n – размер выборки;

Получаем: n = 217.

Поскольку генеральную совокупность можно считать малой, то скорректируем полученное значение объема выборки по формуле:

Подставляя в формулу имеющиеся значения, получаем n’ = 207.

Для того, чтобы гарантировать результат с вероятностью 95,4 % (z = 2), необходимо обследовать 370 семей. Эту величину можно округлить до 400 семей, т.е. устанавливается 4 % выборка.

Условные обозначения для переменных генеральной совокупности.

Формула расчета дисперсии:

Стандартная ошибка среднего (доли) относится к выборочному распределению среднего или доли, а не к выборке или всей совокупности.

Нормированное отклонение z точки – это количество стандартных ошибок, на которые точка удалена от среднего.

Ошибка, степень точности – максимально допустимое различие между выборочным средним и генеральным средним.

Нормальное распределение – симметричный график, колоколообразная форма. Функция нормального распределения задается генеральным средним µ и генеральным стандартным отклонением σ. Существует бесконечное множество комбинаций µ и σ.

Расчет средней ошибки повторной простой случайной выборки производится следующим образом:

cредняя ошибка для средней:

cредняя ошибка для доли:

Расчет средней ошибки бесповторной случайной выборки:

средняя ошибка для средней:

средняя ошибка для доли:

Расчет предельной ошибки повторной случайной выборки:

предельная ошибка для средней:

предельная ошибка для доли:

Расчет предельной ошибки бесповторной случайной выборки:

Источник

Определение объема выборки

На практике решение вопроса об объеме выборки является компромиссным между предположением о точности результатов обследования и возможностями их практической реализации (т.е. исходя из затрат на проведение опроса).

На практике используется несколько подходов к определению объема выборки. Обратим внимание на самые простые из них. Первый из них называется произвольным подходом и основан он на применении «правила большого пальца».

Например, бездоказательно принимается, что для получения точных результатов выборка должна составлять 5 % от совокупности. Данный подход простой и доступный в исполнении, не позволяет получать точные результаты. Его достоинством является относительная дешевизна затрат. В соответствии со вторым подходом объем выборки может быть установлен исходя из заранее оговоренных условий. Заказчик маркетингового исследования, например, знает, что при изучении общественного мнения выборка обычно составляет 1000 – 1200 человек, поэтому он рекомендует исследователю придерживаться данной цифры.

Третий подход означает, что в некоторых случаях главным аргументом при определении объема выборки может быть стоимость проведения опроса. Хотя при этом ценность и достоверность получаемой информации не принимается в расчет.

В случае четвертого подхода объем выборки определяется на основе статистического анализа. Данный подход предполагает определение минимального объема выборки с учетом требований к надежности и достоверности получаемых результатов.

Пятый подход считается наиболее теоретически обоснованным и правильным подходом в определении объема выборки. Он основан на расчете доверительного интервала.

Доверительный интервал – это диапазон, крайние точки которого характеризуют процент определенных ответов на какой-то вопрос. Данное понятие тесто связано с понятием «среднее квадратичное отклонение получаемого признака в генеральной совокупности». Чем оно больше, тем шире должен быть доверительный интервал, чтобы включить в свой состав, например 9,5 % ответов.

Из свойств нормальной кривой распределения вытекает, что конечные точки доверительного интервала, равного к примеру 9,5 % определяются как произведение: 1,96 (нормированное отклонение) и среднего квадратичного отклонения.

Числа 1,96 и 2,58 (для 99 % доверительного интервала) обозначаются как z.

Существуют таблицы «Значение интеграла вероятности», которые дают возможность определить величины z для различных доверительных интервалов. Доверительный интервал равный 95% или 99% является стандартным при проведении маркетинговых исследований.

Например, проведено исследование числа визитов автовладельцев в сервисные мастерские за год. Доверительный интервал для среднего числа визитов был рассчитан равным 5 – 7 визитам при 99 % уровне доверительности. Это означает, что если появится возможность, провести независимо 100 раз выборочные исследования, то для 99 выборочных исследований среднее значение числа визитов попадут в диапазон от 5 до 7 визитов, Если сказать иначе, то 99 % автовладельцев попадут в доверительный интервал.

Допустим, было проведено исследование до 50 независимых выборок. Средние оценки для этих выборок образовали нормальную кривую распределения, которое называется выборочным распределением.

Средняя оценка для совокупности в целом равна средней оценке кривой распределения. Понятие «выборочное распределение» рассматривается также в качестве одного из базовых понятий теоретической концепции, лежащее в основе определения V выборки.

Естественно ни одна компания не в состоянии сформировать 10, 20, 50 независимых выборок. Обычно используется только одна выборка.

Математическая статистика позволяет получить некую информацию о выборочном распределении, владея точными данными о вариации единственной выборки.

Индикатором степени отличия оценки, истинной для совокупности в целом, которая ожидается для типичной выборки, является средне квадратическая ошибка. К примеру, исследуется мнение потребителей о новом товаре и заказчик данного исследования указал, что его устроит точность полученных результатов, равная плюс минус 5%.

Предположим, что 30 % членов выборки высказались за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25 – 35 %. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.

Определим объем выборки на основе расчета доверительного интервала. Исходной информацией, необходимой для реализации данного подхода, является:

Когда на заданный вопрос существует только два варианта ответов, выраженных в процентах (используется процентная мера), объем выборки определяется по следующей формуле:

где n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности (табл. 7);

р – найденная вариация для выборки;

е – допустимая ошибка.

Значение нормированного отклонения оценки z от среднего значения

в зависимости от доверительной вероятности (а) полученного результата

Источник

Определение объема выборки

Ранее мы рассмотрели методы построения доверительного интервала для математического ожидания генеральной совокупности. В каждом из рассмотренных случаев мы заранее фиксировали объем выборки, не учитывая ширину доверительного интервала. В реальных задачах определить объем выборки довольно сложно. Это зависит от наличия финансовых ресурсов, времени и легкости создания выборки. [1] Например, если нам необходимо оценить среднюю сумму накладных или долю ошибочных накладных в информационной системе компании, сначала следует выяснить, насколько точной должна быть оценка. Иначе говоря, следует задать ошибку выборочного исследования, допускаемую при оценке каждого из параметров. Кроме того, необходимо заранее определить доверительный уровень оценки истинного параметра генеральной совокупности.

Определение объема выборки для оценки математического ожидания

Чтобы определить объем выборки, необходимый для оценки математического ожидания генеральной совокупности, следует учесть величину ошибки выборочного исследования и доверительный уровень. Кроме того, необходима дополнительная информация о величине стандартного отклонения. Для того чтобы вывести формулу, позволяющую вычислить объем выборки, начнем с формулы (1) (о происхождении этой формулы см. Построение доверительного интервала для математического ожидания генеральной совокупности):

где – среднее значение выборки, Z — значение стандартизованной нормально распределенной случайной величины, соответствующее интегральной вероятности, равной 1 – α/2, σ — стандартное отклонение генеральной совокупности, n – объем выборки

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

В этой формуле величина, добавляемая и вычитаемая из равна половине длины интервала. Она определяет меру неточности оценки, возникающей вследствие ошибки выборочного исследования, которая обозначается символом е и вычисляется по формуле

Решив уравнение (2) относительно n, получим:

Таким образом, для определения объема выборки необходимо знать три параметра:

На практике вычислить эти величины непросто. Как определить доверительный уровень и ошибку выборочного исследования? Обычно ответить на этот вопрос могут лишь эксперты в предметной области (т.е. люди, понимающие смысл оцениваемых величин). Как правило, доверительный уровень равен 95% (в этом случае Z = 1,96). [3] Если требуется поднять доверительный уровень, обычно выбирают величину, равную 99%. Если можно ограничиться более низким доверительным уровнем, выбирают 90%. Определяя ошибку выборочного исследования, не стоит думать о ее величине (в принципе, любая ошибка нежелательна). Следует задать такую ошибку, чтобы полученные результаты допускали разумную интерпретацию.

Кроме доверительного уровня и ошибки выборочного исследования, необходимо знать стандартное отклонение генеральной совокупности. К сожалению, этот параметр почти никогда не известен. В некоторых случаях стандартное отклонение генеральной совокупности можно оценить на основе предшествующих исследований. В других ситуациях эксперт может учесть размах выборки и распределение случайной переменной. Например, если генеральная совокупность имеет нормальное распределение, ее размах приближенно равен 6σ (т.е. ±3σ в окрестности математического ожидания). Следовательно, стандартное отклонение приближенно равно одной шестой части диапазона. Если величину σ невозможно оценить таким способом, необходимо выполнить пилотный проект и вычислить стандартное отклонение по результатам.

Пример 1. Вернемся к задаче об аудиторской проверке. Предположим, что из информационной системы извлечена выборка, состоящая из 100 накладных, заполненных в течение последнего месяца. Компания желает построить интервал, содержащий математическое ожидание генеральной совокупности, доверительный уровень которого равен 95%. Как был определен объем выборки? Следует ли его уточнить?

Допустим, что после консультаций с экспертами, работающими в компании, статистики установили допустимую ошибку выборочного исследования равной ±5 долл., а доверительный уровень — 95%. Результаты предшествующих исследований свидетельствуют, что стандартное отклонение генеральной совокупности приближенно равно 25 долл. Таким образом, е = 5, σ = 25 и Z = 1,96 (что соответствует 95%-ному доверительному уровню). По формуле (3) получаем:

Следовательно, n = 96. Таким образом, объем выборки, равный 100, был выбран удачно и вполне соответствует требованиям, выдвинутым компанией.

Пример 2. Некая промышленная компания на Среднем Западе производит электрические изоляторы. Если во время работы изолятор выходит из строя, происходит короткое замыкание. Чтобы проверить прочность изолятора, компания проводит испытания, в ходе которых определяется максимальная сила, необходимая для разрушения изолятора. Сила измеряется в фунтах нагрузки, приводящей к разрушению изолятора (рис. 1, столбец А). Предположим, что нам необходимо оценить среднюю силу разрушения изолятора с точностью +25 фунтов при 95%-ном доверительном интервале для этой величины. Данные, полученные в предыдущем исследовании, свидетельствуют, что стандартное отклонение равно 100 фунтов. Определите требуемый объем выборки.

Решение. Итак, е = 25, σ =100, доверительный уровень 95% (т.е. Z = 1,96) (рис. 1).

Рис. 1. Определение объема выборки

Таким образом, n = 62 (дробные результаты, как правило, округляют с избытком до ближайшего целого).

Определение объема выборки для оценки доли признака в генеральной совокупности

Выше мы рассмотрели способ определения объема выборки для оценки математического ожидания генеральной совокупности. Предположим теперь, что нам необходимо определить долю накладных, не соответствующих правилам, принятым компанией (начальные условия см. пример 1 выше). Сколько накладных следует извлечь из информационной системы, чтобы построенный интервал имел заданный доверительный уровень? Для ответа на этот вопрос применим тот же подход, что и при определении объема выборки для оценки математического ожидания.

Выражая n через остальные величины, получаем следующую формулу:

Таким образом, для определения объема выборки необходимо знать три параметра:

На практике вычислить эти величины нелегко. Если известен доверительный уровень, можно вычислить критическое значение стандартизованного нормального распределения Z. Ошибка выборочного исследования е определяет точность, с которой оценивается доля успехов в генеральной совокупности. Третий параметр — доля успехов в генеральной совокупности р — это именно тот параметр, который нам необходимо оценить. Итак, как оценить диапазон изменения величины р по его выборочным значениям?

Существуют два способа. Во-первых, во многих ситуациях для оценки величины р можно использовать результаты предыдущих исследований. Во-вторых, если данные о предыдущих исследованиях недоступны, можно попытаться оценить параметр р так, чтобы исключить недооценку объема выборки. Обратите внимание на то, что в формуле (5) величина р(1 – р) стоит в числителе. Следовательно, необходимо найти максимальное значение этой величины. Очевидно, что оно достигается при р = 0,5.

Таким образом, если доля признака в генеральной совокупности р заранее неизвестна, для определения объема выборки следует задать р = 0,5. В этом случае объем выборки будет переоценен, что приведет к дополнительным затратам на ее создание. Если истинная доля успехов в генеральной совокупности сильно отличается от 0,5, доверительный интервал окажется значительно уже, чем требовалось. Оценка параметра р в этом случае будет весьма точной, однако за это придется заплатить дополнительными временными и финансовыми ресурсами.

Вернемся к задаче об аудиторской проверке. Предположим, аудитор желает построить интервал, содержащий долю ошибочных накладных, доверительный уровень которого равен 95%. Допустимая точность равна ±0,07. Результаты предыдущих проверок свидетельствуют, что доля ошибочных накладных не превышает 0,15. Таким образом, е = 0,07, р = 0,15 и Z = 1,96 (что соответствует 95%-ному доверительному уровню). По формуле (5) получаем:

Таким образом, объем выборки, равный 100, был выбран совершенно правильно и вполне соответствует требованиям, выдвинутым компанией.

Определение объема выборки, извлекаемой из конечной генеральной совокупности

Для определения объема выборки, извлеченной из конечной генеральной совокупности без возвращения, необходимо использовать поправочный коэффициент. Например, при оценке математического ожидания выборочная ошибка вычисляется по следующей формуле:

При оценке доли признака ошибка выборочного исследования равна:

Чтобы вычислить объем выборки для оценки математического ожидания или доли признака, применяются формулы:

где n₀ — объем выборки без учета поправочного коэффициента для конечной генеральной совокупности. Применение поправочного коэффициента приводит к следующей формуле:

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 471–476

[2] Для определения размера выборки используется величина Z, а не t, поскольку для вычисления критического значения t размер выборки необходимо знать заранее. В большинстве случаев размеры выборки позволяют хорошо аппроксимировать t-распределение стандартизованным нормальным распределением.

[3] Интервал c доверительным уровнем 95% делится на две равные части. Первая часть лежит слева от математического ожидания генеральной совокупности, а вторая — справа. Значение величины Z, соответствующей вероятности 2,5% (площади 0,025), равно –1,96, а значение величины Z, соответствующей суммарной площади 0,975, равно +1,96. Для расчета удобно воспользоваться функцией Excel Z=НОРМ.СТ.ОБР(р), где р – вероятность, подставляя значения р₁ = 2,5% и р₂ = 97,5%

13 комментариев для “Определение объема выборки”

Предположим, суммарная стоимость всех элементов (счетов-фактур, объектов основных средств, запасов и т. д.) составляет 200 000 тыс. тенге. Суммарное денежное выражение элементов наибольшей стоимости — 4 000 тыс. тенге. Суммарное денежное выражение ключевых элементов — 6 000 тыс. тенге. Уровень существенности — 5 000 тыс. тенге. Аудиторский риск составляет 10%, соответственно, уровень надежности — 90%.
1. Найти объем выборки

По какой формуле определяется объем выборки, если заранее известны генеральная совокупность и распределение оценок&

Света, обратитесь к примерам 1 и 2 настоящей заметки. Откройте Excel-файл, в нем есть формулы. Если останутся вопросы, пришлите в личку исходные данные.

Добрый день!
Перерыла весь интернет, так и не смогла вспомнить, как решить следующую задачу:

Недавно нанятый менеджер Яндекса должен посчитать, какая доля пользователей из России имеет доход больше 40 000 руб. в месяц. Для этого он через специальную форму на странице http://www.yandex.ru может анонимно опрашивать пользователей об их доходе. Специалисты из поиска считают, что такие опросы мешают пользователям и тем самым портят качество сервиса. Какое минимальное количество людей менеджер должен опросить, чтобы посчитать долю с точностью в пределах одного процентного пункта на уровне доверия 95 %? Дисперсию оценки искомой доли следует считать максимальной, а квантиль 0.975 нормального распределения —приблизительно равной двум.

Ну что вы, что вы. неужели так сложно самому цифры подставить, али вы гуманитарий совсем?

Помоги пожалуйста решить: Оценить объем репрезентативной выборочной совокупности с ошибкой не более 10%, если в качестве генеральной совокупности выступает население города от 100 до 120 тысяч человек.

Каким должен быть объем выборки при случайном повторном отборе, чтобы ошибка определения среднего (среднее квадратичное отклонение оценки от истинного среднего) составляла не более 10% от среднего квадратичного отклонения в генеральной совокупности? Помогите, пожалуйста

Источник