Чем определяется надежность криптосистемы
Надежность использования криптосистем
В компьютерном и околокомпьютерном мире все время появляется информация об ошибках или «дырах» в той или иной программе (в том числе применяющей криптоалгоритмы), или о том, что такие программы были взломаны. Это создает недоверие как к конкретным программам, так и к возможности вообще защитить что-либо криптографическими методами не только от спецслужб, но и от простых хакеров.
На сегодняшний день существуют хорошо известные и апробированные криптоалгоритмы (как с симметричными, так и несимметричными ключами), крип-тостойкость которых либо доказана математически, либо основана на необходимости решения математически сложной задачи (факторизации, дискретного
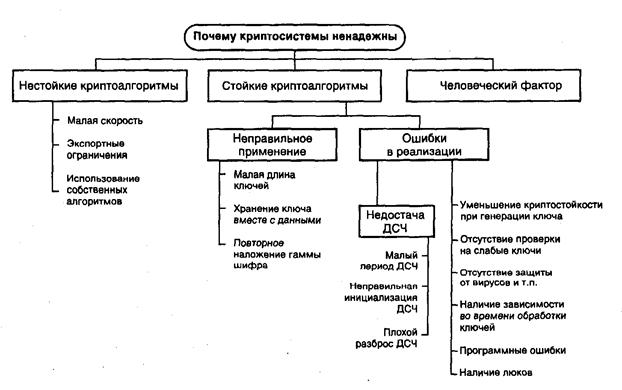
Рис. 5.30. Причины ненадежности криптосистем
логарифмирования и т. п.). К наиболее известным из них относятся DES, RSA, ГОСТ. Таким образом, они не могут быть вскрыты иначе, чем полным перебором или решением указанной задачи. Но тем не менее, можно выделить следующие основные группы причин ненадежности криптографи-ческих систем:
• Применение нестойких алгоритмов
• Ошибки в реализации криптоалгоритмов
• Неправильное применение криптоалгоритмов
При этом видна четкая параллель между ними и причинами нарушения безопасности вычислительных систем. Более подробно причины ненадежности криптосистем представлена на рис. 5.30. Из-за них имелись или имеются проблемы безопасности у всех классов программных продуктов, использующих криптоалгоритмы, будь то операционные системы; криптопротоколы; клиенты и сервера, их поддерживающие; офисные программы; пользовательские утилиты шифрования; популярные архиваторы.
Научный подход к анализу криптостойкости шифров приобрел стройность после публикации в 1949 году работы К. Шеннона «Теория связи в секретных системах». Он предложил рассматривать криптостойкость систем с двух точек зрения — теоретической (совершенной) и практической (вычислительной) стойкости.
С точки зрения теоретической стойкости рассматривается насколько надежна некоторая криптосистема, если криптоаналитик, ее вскрывающий, не ограничен временем и обладает всеми необходимыми средствами. Теоретическая криптостойкость использует два допущения: криптоаналитику известна только шифрованная информация и ключ используется только один раз. Решение этого вопроса приводит к следующему выводу: объем секретного ключа для построения теоритической стойкости шифра недопустимо велик для большинства практических применений.
С точки зрения вычислительной стойкости рассматривается надежна ли некоторая криптосистема, если криптоаналитик располагает ограниченным временем и вычислительными возможностями для анализа шифрованной информации.
• В шифротексте сохраняются статистические зависимости символов и сочетаний символов исходного текста
• Перемешанный относительный алфавит может быть установлен постепенным подбором.
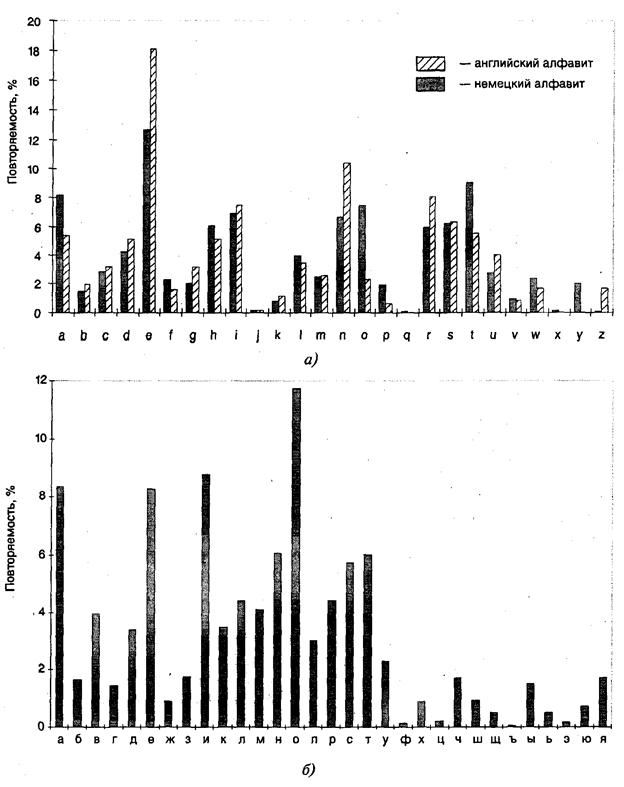
Для любого естественного языка частота встречаемости букв в тексте различна, вспомните, например, телеигру «Поле чудес». Частота встречаемости букв в процентах от общего количества символов в сообщении для русского, английского и немецкого алфавитов наглядно представлена на рис 5.31.
Кроме того на основании анализа частоты встречаемости различных букв шифротекста можно установить, на каком языке написано исходное сообщение. Как видно из рис. 5.31, одни и те же буквы используются с различной частотой. Например, буква Q очень редко встречается в английском и немецком языках, и заметно чаще в итальянском и французском. Буква О активно используется в русском, английском, итальянском, испанском и португальском языках, но реже во французском и немецком. Все это позволяет достаточно быстро расшифровывать простые шифры. Но вернемся к рис. 5.30.
Малая скорость стойких криптоалгоритмов — это основной фактор, затрудняющий применение хороших алгоритмов, например, в системах «тотального» шифрования или шифрования «на лету». В частности, программа Norton DiskReet, хотя и имеет реализацию криптоалгоритма DES, при смене пользователем ключа может не перешифровывать весь диск, так как это займет слишком много времени. Аналогично, программа компрессии «на лету» Stacker фирмы Stac Electronics имеет опцию закрытия паролем компрессируемых данных. Однако она не имеет физической возможности зашифровать этим паролем свой файл, обычно имеющий размеры в несколько сот мегабайт, поэтому она ограничивается очень слабым алгоритмом и
Рис. 5.31. Частота использования букв: а — английского и немецкого алфавитов;
6 — русского алфавита
Экспортные ограничения криптоалгоритмов приводят к тому, что при межгосударственном общении возможно использование только весьма условно защищенных алгоритмов, с временем перебора паролей в среднем около 4 месяцев.
В случае неправильной реализации криптоалгоритмов, несмотря на то, что в этом случае применяются криптостойкие или сертифицированные алгоритмы, эта группа причин приводит к нарушениям безопасности криптосистем.
Такая причина, как уменьшение криптостойкости системы при генерации ключа основана на том, что криптосистема либо обрезает пароль пользователя, либо генерирует из него данные, имеющие меньшее количество бит, чем сам пароль. В старых версиях UNIX пароль пользователя обрезается до 8 байт перед хэшированием. Любопытно, что, например, Linux 2.0, требуя от пользователей ввода паролей, содержащих обязательно буквы и цифры, не проверяет, чтобы 8-символьное начало пароля также состояло из букв и цифр. Поэтому пользователь, задав, например, достаточно надежный пароль passwordlsgoodl 9, будет весьма удивлен, узнав, что хакер вошел в систему под его именем с помощью элементарного пароля password. Novell Netware позволяет пользователям иметь пароли до 128 байт, что дает (считая латинские буквы без учета регистра, цифры и спецсимволы) 68 Ш или 2™ комбинаций. Но при этом, во-первых, хэш-функция получает на входе всего лишь 32-байтовое значение, что ограничивает эффективную длину пароля этой же величиной. Более того, во-вторых, на выходе хэш-значение имеет длину всего 128 бит, что соответствует 2 128 комбинаций. Это дополнительно снижает эффективную длину до 21 символа, то есть в 6 раз по сравнению с первоначальной. Полностью аналогичная ситуация происходит с архиватором RAR версий 1.5х — выбор пароля больше 10 символов не приводит к росту времени, необходимого на его вскрытие.
Недостаточная защищенность от компьютерных вирусов, «троянских коней», программных закладок и прочих программ, способных перехватить секретный ключ или сами нешифрованные данные, а также просто подменить алгоритм на некриптостойкий, приводит к нарушению безопасности криптосистемы. Особенно это актуально для операционных систем, не имеющих встроенных средств защиты или средств разграничения доступа — типа MS DOS или Windows 95. Как пример можно привести самый старый способ похищения пароля, известный еще со времен больших ЭВМ, когда программа-«фантом» эмулирует приглашение ОС, предлагая ввести имя пользователя и пароль, запоминает его в некотором файле и прекращает работу с сообщением «Invalid password». Для MS DOS и Windows существует множество закладок для чтения и сохранения паролей, набираемых на клавиатуре. Примером реализации подмены криптоалгоритма является закладка, маскируемая под прикладную программу-«ускоритель» типа Turbo Krypton. Эта закладка заменяет алгоритм шифрования ГОСТ 28147-89, реализуемой платой «Krypton-З» (демонстрационный вариант), другим, простым и легко дешифруемым алгоритмом. Последним примером служит имевшие место в июне 1998 года попытки проникновения «троянского коня» через электронную почту. В письмо были вложены порнографическая картинка и ЕХЕ-файл FREECD.EXE, который за то время, пока пользователь развлекался с письмом, расшифровывал пароли на соединение с провайдером (Dial-Up) и отправлял их на адрес ispp@usa.net.
Сравнительно новый аспект недостаточно корректной реализации криптоалгоритмов заключается в наличии зависимости во времени обработки ключей. Многие криптосистемы неодинаково быстро обрабатывают разные входные данные. Это происходит как из-за аппаратных (разное количество тактов на операцию, попадание в процессорный кэш и т.п.), так и программных причин (особенно при оптимизации программы по времени). Время может зависеть как от ключа шифрования, так и шифруемых или расшифруемых данных. Поэтому злоумышленник, обладая детальной информацией о реализации криптоалгоритма, имея зашифрованные данные и будучи способным каким-то образом измерять время обработки этих данных (например, анализируя время отправки пакетов с данными), может попытаться подобрать секретный ключ.
Ясно, что пока программы будут писаться людьми, ошибки в программной реализации всегда будут иметь место. Хороший пример — ОС Novell Netware 3.12, где, несмотря на достаточно продуманную систему аутентификации, при которой, по заявлениям фирмы Novell, «нешифрованный пароль никогда не передается по сети», удалось найти ошибку в программе SYSCON v. 3.76, при которой пароль именно в открытом виде попадает в один из сетевых пакетов. Этого не наблюдается ни с более ранними, ни с более поздними версиями этой программы, что позволяет говорить именно о чисто программистской ошибке. Этот ошибка проявляется только если супервизор меняет пароль кому-либо (в том числе и себе). Видимо, каким-то образом в сетевой пакет ропадает клавиатурный буфер.
Причины наличия люков в криптосистемах очевидны: разработчик хочет иметь контроль над обрабатываемой в его системе информацией и оставляет для себя возможность расшифровывать ее, не зная ключа пользователя. Возможно также, что они используются для отладки и по какой-то причине не убираются из конечного продукта. Естественно, что это рано или поздно становится известным достаточно большому кругу лиц и ценность такой криптосистемы становится почти нулевой. Самыми известными примерами здесь являются AWARD BIOS (до версии 4.51PG) с его универсальным паролем «A WARD_SW» и СУБД Paradox фирмы Borland International, также имеющая «суперпароли» «jIGGAe» и «пхббррх». Вплотную к наличию люков в реализации (очевидно, что в этом случае они используют явно нестойкие алгоритмы или хранят ключ вместе с данными) примыкают алгоритмы, дающие возможность третьему лицу читать зашифрованное сообщение, как это сделано в нашумевшем проекте CLIPPER, где третьим лицом выступает государство, всегда любящее совать нос в тайны своих граждан.
Хороший, математически проверенный и корректно реализованный датчик случайных чисел (ДСЧ) также важен для криптосистемы, как и хороший, математически стойкий и корректный криптоалгоритм, иначе его недостатки могут повлиять на общую криптостойкость системы. При этом для моделирования ДСЧ на ЭВМ обычно применяют датчики псевдослучайных чисел (ПСЧ), характеризующиеся периодом, разбросом, а также необходимостью его инициализации (seed). Применение ПСЧ для криптосистем вообще нельзя признать удачным решением, поэтому хорошие криптосистемы применяют для этих целей физический ДСЧ (специальную плату), или, по крайней мере, вырабатывают число для инициализации ПСЧ с помощью физических величин (например, времени нажатия на клавиши пользователем). Малый период и плохой разброс относятся к математическим недостаткам ДСЧ и появляются в том случае, если по каким-то причинам выбирается собственный ДСЧ. Иначе говоря, выбор собственного ДСЧ так же опасен, как и выбор собственного криптоалгоритма. В случае малого периода (когда псевдослучайных значений, вырабатываемых датчиком, меньше, чем возможных значений ключа) злоумышленник может сократить время поиска ключа, перебирая не сами ключи, а псевдослучайные значения и генерируя из них ключи.
Такая группа причин, как неправильное применение криптоалгоритмов, приводит к тому, что оказывается ненадежными криптостойкие и корректно реализованные алгоритмы. Самая очевидная причина — это малая длина ключа. Стойкие криптоалгоритмы могут иметь малую длину ключа вследствие двух факторов:
• Некоторые алгоритмы могут работать с переменной длиной ключа, обеспечивая разную криптостойкость,— и именно задача разработчика выбрать необходимую длину, исходя из желаемой крип-тостойкости и эффективности. Иногда на это желание накладываются и иные обстоятельства — такие, как экспортные ограничения
• Некоторые алгоритмы разрабатывались весьма давно, когда длина используемого в них ключа считалась более чем достаточной
для соблюдения нужного уровня защиты.
Ошибочный выбор класса алгоритма — это также весьма распространенная причина, при которой разработчик выбирает пусть и хороший, но совершенно неподходящий к его задаче алгоритм. Чаще всего это выбор шифрования вместо хэширования или выбор симметричного алгоритма вместо алгоритма с открытыми ключами. Примеров здесь масса — это почти все программы, ограничивающие доступ к компьютеру паролем при его включении или загрузке, например AMI BIOS, хранящий вместо хэша пароля его зашифрованный вариант, который, естественно, легко дешифруется. Во всех сетевых процедурах аутентификации естественно применять ассиметричную криптографию, которая не позволит подобрать ключ даже при полном перехвате трафика. Однако многие программы довольствуются (в лучшем случае!) стандартной схемой «запрос-отклик», при которой можно вести достаточно быстрый перебор по перехваченным значениям «запроса» и «отклика».
Хранение ключа вместе с данными приводит к тому, что данные, зашифрованные с помощью криптостойкого и корректно реализованного алгоритма, могут быть легко дешифрованы. Это связано со спецификой решаемой задачи, при которой невозможно вводить ключ извне и он хранится где-то внутри в практически незашифрованном виде. Иначе говоря, здесь наиболее уязвимым будет алгоритм шифрования не ключом, а ключа (с помощью некоего вторичного ключа). Но так как (что опять-таки очевидно следует из специфики задачи) этот вторичный ключ хранить извне нельзя, то основные данные рано или поздно будут расшифрованы без использования методов перебора. Типичным примером здесь будут все WWW-, ftp-, e-mail-клиенты. Дело в том, что для базовой (наиболее часто встречающейся) аутентификации в этих протоколах пароль должен передаваться серверу в открытом виде. Поэтому клиентские программы вынуждены шифровать (а не хэшировать) пароль, причем с фиксированным ключом, чтобы не надоедать пользователю постоянными вопросами. Отсюда следует, что где-то внутри любого броузера, почтового или ftp-клиента (будь то Netscape Communicator, Eudora, Outlook, FAR и т. п.) лежат все ваши пароли в практически открытом виде, и что расшифровать их не представляет труда. (Чаще всего, кстати, пароль в таких программах даже не шифруется, а кодируется алгоритмом типа base-64.)
В любой критической системе ошибки человека-оператора являются чуть ли не самыми дорогостоящими и распространенными. В случае криптосистем непрофессиональные действия пользователя сводят на нет самый стойкий криптоалгоритм и самую корректную его реализацию и применение.
В первую очередь это связано с выбором паролей. Очевидно, что короткие или осмысленные пароли легко запоминаются человеком, но они гораздо проще для вскрытия. Использование длинных и бессмысленных паролей безусловно лучше с точки зрения криптостойкости, но человек обычно не может их запомнить и записывает на бумажке, которая потом либо теряется, либо попадает в руки злоумышленнику. Именно из того, что неискушенные пользователи обычно выбирают либо короткие, либо осмыслен-Т5Б£, та^сщц ^wi^cwpoT даа «метода, та ъск^ътлж.
• Атака полным перебором
В связи с резким ростом вычислительных мощностей атаки полным перебором имеют гораздо больше шансов на успех, чем раньше. Если для системы UNIX функция crypt(), которая отвечает за хэширование паролей, была реализована так, что выполнялась почти 1 секунду на машину класса PDP, то за двадцать лет скорость ее вычисления увеличилась в 15 000 раз. Поэтому если раньше хакеры (и разработчики, которые ограничили длину пароля 8 символами) и представить себе не могли полный перебор, то сегодня такая атака в среднем приведет к успеху за 80 дней. Скорость перебора паролей для различных криптосистем приведена в табл. 5.3.
Однако вернемся на несколько лет назад, когда вычислительной мощности для полного перебора всех паролей не хватало. Тем не менее, хакерами был придуман остроумный метод, основанный на том, что в качестве пароля человеком выбирается существующее слово или какая-либо инфор-
Таблица 5.3. Скорость полного перебора на компьютере класса Pentium/166.
мация о себе или своих знакомых (имя, дата рождения и т. п.). Ну, а поскольку в любом языке не более 100 000 слов, то их перебор займет весьма небольшое время, и от 40 до 80% существующих паролей может быть угадано с помощью такой простой схемы, называемой «атакой по словарю». (Кстати, до 80% этих паролей может быть угадано с использованием словаря размером всего 1000 слов!). Даже вирус Морриса (в 1988 г.) применял такой способ, тем более что в UNIX «под рукой» часто оказывается файл-словарь, обычно используемый программами-корректорами. Что же касается «собственных» паролей, то файл /etc/passwd может дать немало информации о пользователе: его входное имя, имя и фамилию, домашний каталог. Вирус Морриса с успехом пользовался следующими предположениями:
• В качестве пароля берется входное имя пользователя
• Пароль представляет собой двойной повтор имени пользователя
• То же, но прочитанное справа налево
• Имя или фамилия пользователя
• То же, но в нижнем регистре.
Пусть сегодня пользователи уже понимают, что выбирать такие пароли нельзя, но до тех пор, пока с компьютером работает человек, эксперты по компьютерной безопасности не дождутся использования таких простых и радующих душу паролей, как 34jXs5U@bTa!6. Поэтому даже искушенный пользователь хитрит и выбирает такие пароли, как hopel, user 1997, pAsSwOrD, toor, roottoor, parol, gfhjkm, asxz. Видно, что все они, как правило, базируются на осмысленном слове и некотором простом правиле его преобразования: прибавить цифру, прибавить год, перевести через букву в другой регистр, записать слово наоборот, прибавить записанное наоборот слово, записать русское слово латинскими буквами, набрать русское слово на клавиатуре с латинской раскладкой, составить пароль из рядом расположенных на клавиатуре клавиш и т. п. Поэтому не надо удивляться, если такой «хитрый» пароль будет вскрыт хакерами — они не глупее самих пользователей, и уже вставили в свои программы те правила, по которым может идти преобразование слов.
3 Симметричные криптосистемы и блочные шифры
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Оценка надежности криптосистем
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра прикладной математики и информатики
К У Р С О В А Я Р А Б О Т А
Современные криптографические методы
Студент IV-ИЭ-8 Альперт В. В.
Научный руководитель Пономарев В. П.
С О Д Е Р Ж А Н И Е
Введение в криптографию______________________________________________ 3
Симметричные криптосистемы___________________________________________ 5
Стандарт шифрования данных ГОСТ 28147-89______________________________ 6
Международный алгоритм шифрования данных IDEA_______________________ 10
Алгоритм RSA_______________________________________________________ 12
Оценка надежности криптосистем_______________________________________ 14
Введение в криптографию
Бурное развитие криптографические системы получили в годы первой и второй мировых войн. Начиная с послевоенного времени и по нынешний день, появление вычислительных средств ускорило разработку и совершенствование криптографических методов.
Проблема использования криптографических методов в информационных системах стала в настоящий момент особо актуальна потому, что с одной стороны, расширилось использование компьютерных сетей, в частности глобальной сети Интернет, по которым передаются большие объемы информации государственного, военного, коммерческого и частного характера, не допускающего возможность доступа к ней посторонних лиц.
С другой стороны, появление новых мощных компьютеров, технологий сетевых и нейронных вычислений сделало возможным дискредитацию криптографических систем еще недавно считавшихся практически не раскрываемыми.
Криптография занимается поиском и исследованием математических методов преобразования информации.
 |
 |
Криптосистемы разделяются на симметричные и системы с открытым ключом. В симметричных криптосистемах и для шифрования, и для дешифрования используется один и тот же ключ.
Электронной (цифровой) подписью называется присоединяемое к тексту его криптографическое преобразование, которое позволяет при получении текста другим пользователем проверить авторство и подлинность сообщения.
Криптостойкостью называется характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа (т.е. криптоанализу). Имеется несколько показателей криптостойкости, среди которых:
· количество всех возможных ключей;
· среднее время, необходимое для криптоанализа.
Криптография в прошлом использовалась лишь в военных целях. Однако сейчас, с становлением информационного общества, она становится центральным инструментом для обеспечения конфиденциальности. По мере образования информационного общества, крупным государствам становятся доступны технологические средства тотального надзора за миллионами людей. Поэтому криптография становится одним из основных инструментов обеспечивающих конфиденциальность, доверие, авторизацию, электронные платежи, корпоративную безопасность и бесчисленное множество других важных вещей.
Все многообразие существующих криптографических методов можно свести к следующим классам преобразований:
 | ||
 |  | |
Моно- и полиалфавитные подстановки.
Наиболее простой вид преобразований, заключающийся в замене символов исходного текста на другие (того же алфавита) по более или менее сложному правилу. Для обеспечения высокой криптостойкости требуется использование больших ключей.
Также несложный метод криптографического преобразования. Используется, как правило, в сочетании с другими методами.
Этот метод заключается в наложении на исходный текст некоторой псевдослучайной последовательности, генерируемой на основе ключа.
Представляют собой последовательность (с возможным повторением и чередованием) основных методов преобразования, применяемую к блоку (части) шифруемого текста. Блочные шифры на практике встречаются чаще, чем “чистые” преобразования того или иного класса в силу их более высокой криптостойкости. Российский и американский стандарты шифрования основаны именно на этом классе шифров.
Стандарт шифрования данных ГОСТ 28147-89
Российский стандарт шифрования является блочным, т. е. преобразование ведется по блокам. Он включает в себя режим замены и два режима гаммирования. Стандарт ГОСТ 28147-89 формировался с учетом мирового опыта, и в частности, были приняты во внимание недостатки и нереализованные возможности алгоритма DES, поэтому использование стандарта ГОСТ предпочтительнее. Эффективность данного стандарта достаточно высока. Системы, основанные на ГОСТ 28147-89, позволяют зашифровать в секунду до нескольких десятков Кбайт данных. В него заложен метод, с помощью которого можно зафиксировать необнаруженную случайную или умышленную модификацию зашифрованной информации.
Алгоритм криптографического преобразования предусматривает три режима работы. В стандарте ГОСТ используется ключ W длиной 256 бит, представляемый в виде восьми 32-разрядных чисел x(i).
Пусть открытые блоки разбиты на блоки по 64 бит в каждом, которые обозначим как T(j).
Очередная последовательность бит T(j) разделяется на две последовательности B(0) и A(0) по 32 бита (правый и левый блоки). Далее выполняется итеративный процесс шифрования, описываемый следующими формулами, вид который зависит от i.
Для дешифрования используется тот же ключ, но процесс дешифрования является инверсным по отношению к исходному.
Полученные A(0), B(0) – расшифрованный текст.
Здесь i обозначает номер итерации. Функция f – функция шифрования.
Функция шифрования состоит из операции подстановки К применяемой к 32-разрядному аргументу. 64-разрядный аргумент разбивается на два 32-разрядных вектора. Блок подстановки K состоит из 8 узлов замены К(1). К(8) с памятью 64 бит каждый. Поступающий на блок подстановки 4-разрядный вектор разбивается на 8 последовательно идущих 4-разрядных векторов, каждый из которых преобразуется в 4-разрядный вектор соответствующим узлом замены, представляющим таблицу из 16 целых чисел в диапазоне 0. 15. Входной вектор определяет адрес строки в таблице, число из которой является выходным вектором. Затем 4-разрядные векторы последовательно объединяются в 32-разрядный выходной.
Остальные блоки открытых данных в режиме простой замены зашифровываются аналогично.
Следует учитывать, что данный режим шифрования обладает ограниченной криптостойкостью.
Другой режим шифрования называется режимом гаммирования.
Открытые данные, разбитые на 64-разрядные блоки T(i) (i=1,2. m) (m определяется объемом шифруемых данных), зашифровываются в режиме гаммирования путем поразрядного сложения по модулю 2 с гаммой шифра Гш, которая вырабатывается блоками по 64 бит, т.е.
Уравнение шифрования данных в режиме гаммирования может быть представлено в следующем виде:
64-разрядная последовательность, называемая синхропосылкой, не является секретным элементом шифра, но ее наличие необходимо как на передающей стороне, так и на приемной.
Режим гаммирования с обратной связью очень похож на режим гаммирования. Как и в режиме гаммирования открытые данные, разбитые на 64-разрядные блоки T(i), зашифровываются путем поразрядного сложения по модулю 2 с гаммой шифра Гш, которая вырабатывается блоками по 64 бит:
Уравнение шифрования данных в режиме гаммирования с обратной связью выглядят следующим образом:
Для получения имитовставки открытые данные представляются также в виде блоков по 64 бит. Первый блок открытых данных Т(1) подвергается преобразованию, соответствующему первым 16 циклам алгоритма режима простой замены. В качестве ключа используется тот же ключ, что и для шифрования данных. Полученное 64-разрядное число суммируется побитно с открытым блоком Т(2) и сумма вновь подвергается 16 циклам шифрования для режима простой замены. Данная процедура повторятся для всехблоков сообщения. Из полученного 64-разрядного числа выбирается отрезок Ир длиной р бит.
Имитовставка передается по каналу связи после зашифрованных данных. На приемной стороне аналогичным образом из принятого сообщения выделяется имитовставка и сравнивается с полученной. В случае несовпадения имитовставок сообщение считается ложным.
КОНСТАНТЫ C1=1538417 341, C2=2591989193
ТАБЛИЦА ПОДСТАНОВОК Kij
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| K(1) | 1 | 0 | 0 | 1 | 5 | 9 | 8 | 4 | 6 | 5 | 2 | 3 | 13 | 12 | 7 | 4 |
| K(2) | 0 | 3 | 8 | 1 | 11 | 13 | 6 | 10 | 2 | 15 | 7 | 4 | 14 | 5 | 12 | 9 |
| K(3) | 4 | 7 | 13 | 5 | 0 | 3 | 12 | 1 | 9 | 8 | 10 | 14 | 6 | 2 | 11 | 15 |
| K(4) | 10 | 15 | 2 | 12 | 9 | 14 | 7 | 6 | 8 | 4 | 0 | 13 | 3 | 11 | 5 | 1 |
| K(5) | 6 | 1 | 4 | 10 | 2 | 12 | 0 | 15 | 8 | 13 | 3 | 11 | 5 | 9 | 14 | 7 |
| K(6) | 8 | 11 | 7 | 14 | 15 | 5 | 12 | 2 | 0 | 9 | 10 | 1 | 6 | 13 | 3 | 4 |
| K(7) | 11 | 5 | 9 | 4 | 3 | 1 | 15 | 8 | 7 | 2 | 14 | 0 | 13 | 12 | 10 | 6 |
| K(8) | 4 | 13 | 15 | 5 | 0 | 3 | 12 | 7 | 10 | 11 | 8 | 9 | 6 | 1 | 14 | 2 |
Международный алгоритм шифрования данных IDEA
Шифр IDEA (International Data Encryption Algorithm) был разработан Лэй и Мэсси из ETH в Цюрихе. Этот шифр, наряду с RSA, применяется в популярной компьютерной криптосистеме PGP (Pretty Good Privacy).
IDEA представляет собой блочный шифр, использующий 128 битный ключ, для преобразования открытых 64 битных текстовых блоков.
Графическая схема алгоритма IDEA
64 битный текстовый блок подвергается в ходе шифрования следующим процедурам:
Процесс шифрования представляет собой цикл из восьми шагов:
p1, p2, p3, p4 – четыре 16 битных блока, на которые разбиваются один блок исходного текста
s1, s2, s3, s4, s5, s6 – шесть 16 битных подключей.
На следующем шаге в качестве p1, p2, p3, p4 используют d11, d13, d12, d14 и новые шесть подключей. Полученные четыре последние 16 битных блока и есть зашифрованный текст. Процесс дешифрования осуществляется аналогично.
Шифрование и дешифрование отличаются только подключами. Первые восемь подключей определяются с помощью 128 битного ключа, который разделяется на восемь частей. Новые восемь подключей определяются следующим образом: начальный ключ смещается на 25 бит, и разделяется на восемь частей.
Подключи для дешифрования определяются таблицей:
1 шаг s49* s50# s51# s52* s47 s48
2 шаг s43* s45# s44# s46* s41 s42
3 шаг s37* s39# s38# s39* s35 s36
4 шаг s31* s33# s32# s34* s29 s30
5 шаг s25* s27# s26# s28* s23 s24
6 шаг s19* s21# s20# s22* s17 s18
7 шаг s13* s15# s14# s16* s11 s12
8 шаг s7* s9# s8# s10* s5 s6
Последнее преобразование s1* s2# s3# s4*
sXX* = мультипликативная инверсия sXX по модулю 2 16 +1
sXX# = аддитивная инверсия sXX по модулю 2 16
Алгоритм RSA
Для решения этой проблемы на основе результатов, полученных классической и современной алгеброй, были предложены системы с открытым ключом.
Суть их состоит в том, что каждым адресатом ИС генерируются два ключа, связанные между собой по определенному правилу. Один ключ объявляется открытым, а другой закрытым. Открытый ключ публикуется и доступен любому, кто желает послать сообщение адресату. Секретный ключ сохраняется в тайне.
Исходный текст шифруется открытым ключом адресата и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Дешифрование сообщение возможно только с использованием закрытого ключа, который известен только самому адресату.
 |
Асимметричные криптографические системы используют так называемые необратимые или односторонние функции, которые обладают следующим свойством: при заданном значении x относительно просто вычислить значение f(x), однако если y=f(x), то нет простого пути для вычисления значения x.
Алгоритмы шифрования с открытым ключом получили широкое распространение в современных информационных системах. Так, алгоритм RSA стал мировым стандартом де-факто для открытых систем.
Алгоритмы криптосистем с открытым ключом можно использовать в 3 назначениях.
1. Как самостоятельные средства защиты передаваемых и хранимых данных.
2. Как средства для распределения ключей.
3. Средства аутентификации пользователей.
Алгоритмы криптосистем с открытым ключом более трудоемки, чем традиционные криптосистемы, поэтому использование их в качестве самостоятельных средств защиты нерационально.
Поэтому на практике рационально с помощью криптосистем с открытым ключом распределять ключи, объем которых как информации незначителен. А потом с помощью обычных алгоритмов осуществлять обмен большими информационными потоками.
Ривест, Шамир и Эйдельман воспользовались тем фактом, что нахождение больших простых чисел в вычислительном отношении осуществляется легко, но разложение на множители произведения двух таких чисел практически невыполнимо. Доказано (теорема Рабина), что раскрытие шифра RSA эквивалентно такому разложению. Поэтому для любой длины ключа можно дать нижнюю оценку числа операций для раскрытия шифра, а с учетом производительности современных компьютеров оценить и необходимое на это время.
образует открытый ключ, а — закрытый (можно взять и наоборот).
Открытый ключ публикуется и доступен каждому, кто желает послать владельцу ключа сообщение, которое зашифровывается указанным алгоритмом. После шифрования, сообщение невозможно раскрыть с помощью открытого ключа. Владелец же закрытого ключа без труда может расшифровать принятое сообщение.
Шифрование осуществляется по формуле: Sшифр = S e mod N
Шифрование осуществляется по формуле: S = S d шифр mod N
Где S – исходный текст, Sшифр – преобразованный текст, при этом S 16 операций/секунду, а предел роста наступит приблизительно в 2030 г.
Других способов повышения вычислительной мощности нет. Таким образом, с точки зрения защиты информации криптографическими методами, анализ потенциальных возможностей метода распределенных вычислений представляет как для криптоаналитиков, так и для разработчиков криптографических систем значительный интерес. Попробуем, поэтому, проанализировать предельные значения двух указанных тенденций.
Из списка, появившегося летом 1999 года, следует, что по быстродействию суперкомпьютеры распределились следующим образом:
с мощностью порядка 10 12 FLOPS 3 экз.;
с мощностью порядка 10 11 FLOPS 54 экз.;
с мощностью порядка 10 10 FLOPS 428 экз.;
с мощностью порядка 10 9 FLOPS 251 экз.
Десять самых мощных суперкомпьютеров в мире по состоянию на июль 1999 г.
| Рейтинг | Наименование машины | Страна-обладатель | Фирма-производитель | Количество процессоров | Мощность (GFLOPS) |
| 1 | Intel ASCI Red | США | Intel (США) | 9125 | 1333 |
| 2 | Hitachi/Tsukuba CP-PACS | Япония | Hitachi/Tsukuba (Япония) | 2048 | 368 |
| 3 | SGI/Cray T3E | Великобритания | Cray (США) | 696 | 265 |
| 4 | Fujitsu Numerical Wind Tunnel | Япония | Fujitsu (Япония) | 167 | 230 |
| 5 | Hitachi SR2201 | Япония | Hitachi (Япония) | 1024 | 220 |
| 6 | SGI/Cray T3E | Германия | Cray (США) | 512 | 176 |
| 7 | SGI/Cray T3E | США | Cray (США) | 512 | 176 |
| 8 | SGI/Cray T3E | Германия | Cray (США) | 512 | 176 |
| 9 | SGI/Cray T3E | США | Cray (США) | 512 | 176 |
| 10 | SGI/Cray T3E | США | Cray (США) | 512 | 176 |
Первое место в мире по количеству суперкомпьютеров занимают США 254 (51%). За ними следуют Япония 87 (17,5%), Германия 45 (9%), Великобритания 24 (4,8%), Франция 18 (3,6%), Корея 8 (1,6%), Канада 7 (1,4%), Швеция, Швейцария и Норвегия по 6 (1,2%). Россия упомянута в этом списке лишь один раз: на 156-ом месте находится компьютер HPC Ultra 10000 (пиковая производительность 16600 MFLOPS), произведенный фирмой SUN и установленный в Национальном Резервном Банке России. Интересная деталь: в США отсутствуют компьютеры иностранного производства американцы работают только на отечественных машинах и к тому же снабжают ими весь остальной мир.
Количество установок суперкомпьютеров возрастает год от года в геометрической прогрессии, причем основной объем опять же приходится на США. Статистика по годам сложилась следующая:
1999 786 установок
1998 638 установок
1997 207 установок
1996 168 установок
Допустим, что рассматриваемые нами алгоритмы шифрования идеальны, то есть оптимальным методом их взлома будет прямой перебор всех возможных ключей данного алгоритма. Очевидно, что в этом случае стойкость криптосистем будет определяться длиной ключа. При проведении данного исследования предполагалось, что криптоаналитик противной стороны обладает всей информацией относительно алгоритма шифрования, за исключением данных о секретном ключе, и ему доступен для анализа шифрованный текст сообщения. По определению предполагается, что идеальный алгоритм лишен каких-либо недостатков, снижающих его криптостойкость. Для шифров ГОСТ-28147-89 и IDEA существенных недостатков в настоящее время не выявленно.
Предположим также, что генерация ключа компьютером происходит за один такт его работы, а операция дешифрования мгновенно. Определив отношение количества ключей к быстродействию самого мощного компьютера, мы получим нижнюю оценку сложности дешифрования сообщения для идеального алгоритма.
Время, необходимое в настоящий момент самым мощным суперкомпьютерам для полного перебора ключей
| Наименование машины | Мощность (FLOPS) | 56 бит 7.2*Е16 | 64 бита 1.8*E19 | 70 бит 1.18*Е21 | 75 бит 3.78*Е22 | 128 бит 3.4*E38 | 256 бит 1.15*Е77 |
| Intel ASCI Red | 1.333*Е12 | 14 часов | 5 мес. | 28 лет | 899 года | 8.09*Е18 | 2.72*Е57 |
| Hitachi/Tsukuba CP-PACS | 3.68*Е11 | 52 часа | 18 мес. | 102 года | 3257 лет | 2.93*Е19 | 9.9*Е57 |
| SGI/Cray T3E | 2.65*Е11 | 69 часов | 51 мес. | 141 года | 4523 года | 4.07*Е19 | 1.37*Е58 |
| Fujitsu Numerical Wind Tunnel | 2.3*Е11 | 171 час | 60 мес. | 162 года | 5211 года | 4.69*Е19 | 1.58*Е58 |
| Hitachi SR2201 | 2.2*Е11 | 178 часов | 61 мес. | 170 лет | 5448 лет | 4.9*Е19 | 1.66*Е58 |
Оценки трудоемкости разложения простых чисел (1994 год)
| N | Число операций | Длина | Примечания |
| E50 | 1.4*10 10 | 166 бит | Раскрываем на суперкомпьютерах |
| E100 | 2.3*10 15 | 332 бит | На пределе современных технологий |
| E200 | 1.2*10 23 | 664 бит | За пределами современных технологий |
| E300 | 2.7*10 34 | 996 бит | Требует существенных изменений в технологии |
| E500 | 1.3*10 51 | 1660 бит | Не раскрываем |
Оценки трудоемкости разложения простых чисел (2000 год)
| N | Число операций | Длина | Максимальное время дешифровки на суперкомпьютере Intel ASCI Red |
| E50 | 1.4*10 10 | 166 бит | 0.01 сек. |
| E100 | 2.3*10 15 | 332 бит | 29 сек. |
| E200 | 1.2*10 23 | 664 бит | 2854 года |
| E300 | 2.7*10 34 | 996 бит | 6.425*Е14 лет |
| E500 | 1.3*10 51 | 1660 бит | 3.092*Е31 лет |
В конце 1995 года удалось практически реализовать раскрытие шифра RSA для 500-значного ключа. Для этого с помощью сети Интернет было задействовано 1600 компьютеров. Сами авторы RSA рекомендуют использовать следующие размеры модуля N:
Таким образом метод RSA в ближайшее время перестанет использоваться и будет заменен более надежными криптосистемами.
Этому процессору понадобится 1.15*Е51 лет для перебора 256 битного ключа. Более быстрый процессор в нашей вселенной невозможен в принципе, поэтому более быстро производить дешифрование методом тотального перебора ключей принципиально невозможно. Таким образом, прогноз будущего силовой атаки на основе распределенных вычислений неутешителен. Cиловая атака на криптосистемы бесперспективна. Однако, недостатки алгоритмов могут существенно сократить число вариантов перебора. Использование в качестве ключей осмысленных слов позволяет применять атаку по словарю. Следовательно, в дальнейшее развитие криптографии будет происходить в области криптоанализа.
ЗАКЛЮЧЕНИЕ
Хотелось бы отметить, что шифрование и дешифрование востребованы в обществе не сами по себе, а лишь потому, что они могут принести прибыль или позволяют избежать убытков, поэтому всегда необходимо знать какова же стоимость одного знака шифрованной и дешифрованной информации и во что это обходится? Являются ли рентабельными те организации, занимающиеся перехватом и дешифровкой информации, или они заведомо убыточны? Наиболее интересен сравнительный анализ данных с целью научного обоснования доли затрат на защиту информации. При этом также необходимо учитывать, что значительное число атак осуществляется изнутри сотрудниками учреждений, от которых защитится гораздо сложнее. В частности, проблема хранения ключей является в настоящее время наиболее острой и, если использование открытых ключей позволяет решить проблему распределения ключей и аутентификации пользователей, то более эффективного способа хранения ключей, чем запоминание, не найдено, а использование запоминающихся паролей позволяет применить атаку по словарю. Кроме того, использование надежных криптографических методов не гарантирует защиты от программных атак. Следовательно, при создании компьютерных криптосистем необходимо обеспечить безопасность на уровне операционной системы, что является более сложной задачей, чем создание самой криптосистемы.
ЛИТЕРАТУРА
1. Баричев С. Криптография без секретов. М., 1998
2. Брассар Дж. Современная криптология. 1988
3. Жельников В. Криптография от папируса до компьютера. М., 1996
4. Йолнен Тату. Введение в криптографию. 1999
5. Спесивцев А. В. Защита информации в персональных ЭВМ. М., 1992
6. Шнайер Брюс. Прикладная криптография. 1994
Дата добавления: 2019-07-15 ; просмотров: 325 ; Мы поможем в написании вашей работы!