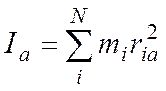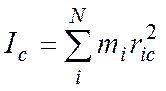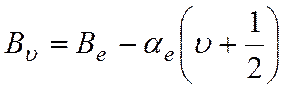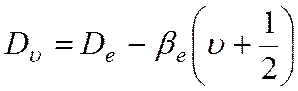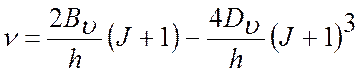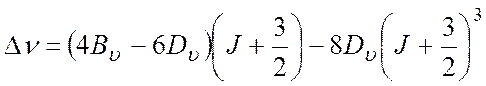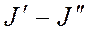Чем определяется межъядерное расстояние в молекулах
УЧЕБНАЯ КНИГА ПО ХИМИИ
ДЛЯ УЧИТЕЛЕЙ СРЕДНИХ ШКОЛ,
СТУДЕНТОВ ПЕДАГОГИЧЕСКИХ ВУЗОВ И ШКОЛЬНИКОВ 9–10 КЛАССОВ,
РЕШИВШИХ ПОСВЯТИТЬ СЕБЯ ХИМИИ И ЕСТЕСТВОЗНАНИЮ
УЧЕБНИК


Продолжение. См. № 4–14, 16–28, 30–34, 37–44, 47, 48/2002;
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22/2003
§ 5.3 Вещество
в кристаллическом состоянии
ЛАБОРАТОРНЫЕ ИССЛЕДОВАНИЯ
1. Определение межъядерного расстояния в кристаллическом железе.
В этой экспериментальной работе вы познакомитесь с определением плотности металла – очень важной характеристикой, благодаря которой можно судить, например, о составе и времени изготовления металлического изделия.
Когда и от кого пошло восклицание «Эврика!»? Древнегреческий ученый Архимед родился в Сиракузах (остров Сицилия) около 287 г. до н. э. и был убит римским солдатом при взятии города во время 2-й Пунической войны. Последние слова Архимеда: «Не трогай мои чертежи». Архимеду приписывают фразу: «Дай мне, где стать, и я сдвину Землю». Архимед нашел решение задачи об определении количества золота и серебра в жертвенной короне сиракузского правителя Гиерона, когда принимал ванну. Он побежал нагим домой с криком «Эврика!», что значит «Нашел!». Попытайтесь в самом общем виде рассказать, как Архимед доказал, что в короне было больше серебра, чем требовалось.
Вам предстоит настоящее научное исследование!
Работу выполняют небольшой группой – 2–4 человека. Внимательно прочитайте описание работы, составьте подробный план эксперимента (имея в наличии образец металла и мерную посуду) и предварительно распределите обязанности (кто что будет делать).
Эксперимент заключается в определении плотности металла, позволяющей, воспользовавшись числом Авогадро, рассчитать межъядерное расстояние, т. е. расстояние между ядрами атомов в кристалле или молекуле. Это расстояние и является одной из постоянных характеристик данного вещества.
Размеры атомов и молекул выражают разными единицами: сантиметрами (см), нанометрами
(1 нм = 1•10 –9 м) и пикометрами (1 пм = 1•10 –12 м). Раньше широко использовали внесистемную единицу длины – ангстрем
Возьмите кусок металла (железа, меди, алюминия, свинца), например, железный шарик от большого подшипника. Можно воспользоваться толстым железным гвоздем, предварительно отпилив его шляпку и острие, чтобы получился цилиндр. Определите взвешиванием массу взятого металла.
Определите объем измеренной массы того же металла. Если имеющийся металл имеет форму правильной геометрической фигуры – куба, шара, цилиндра или другой, измерьте ее размеры линейкой или штангенциркулем. Воспользовавшись математическими познаниями, рассчитайте объем заготовки.
Вы можете взять большую автомобильную гайку или винт, кусок свинцовой оплетки от кабеля. Необязательно брать металл в виде одного куска, можно взять горсть гвоздей, мелких шариков, дроби и т. п. Если вы имеете кусок металла неправильной формы или мелкие куски (шарики, винтики, гайки, гвозди, скрепки и т.п., изготовленные из одного металла, а не сплава), вам следует самим предложить способ определения объема металла известной массы (вы уже успели взвесить горсть или кучку кусочков металла, ничего не потеряв?).
Можно поступить так. Заполните измерительный цилиндр примерно наполовину водой и запишите ее объем (точнее!). Поместите кусочки металла в цилиндр с водой, чтобы вода покрывала металл, и запишите полученный объем воды и металла. Чему равен объем металла? Может случиться, что воды окажется меньше и она не покроет весь металл. Как поступить тогда? Подумайте.
В другой измерительный цилиндр налейте точно известный объем воды и вылейте в цилиндр с металлом столько воды, чтобы она покрывала металл. Запишите положения уровней воды в обоих цилиндрах. Теперь вы можете рассчитать объем воды в цилиндре с металлом и объем, занимаемый водой и металлом. Найдите объем металла и, зная его массу, определите его плотность.
Далее рассчитайте объем, который приходился бы на число Авогадро атомов металла. Определите объем, приходящийся на один атом, и вычислите межъядерное расстояние, приравняв его к длине ребра куба, заключающего внутри себя атом.
Имейте в виду, что этот метод определения межъядерных расстояний приближенный. Тем не менее вычисленные этим методом межъядерные расстояния в кристаллах металлов хорошо совпадают с полученными другими методами.
Вместо железа можно взять другие металлы – медь, свинец, даже золото и серебро.
Как определить размеры одного атома, например, железа? Вам известно, что 1 моль Fe имеет массу
55,845 г.; плотность железа была определена ранее экспериментально. (По справочным данным кристаллическое железо имеет плотность= 7,87 г/см 3 ). Вычислим объем 1 моль железа:
Определим объем, приходящийся на долю одного атома в кристаллической структуре железа. Для этого разделим объем 1 моль атомов (мольный объем) на число Авогадро атомов:
Будем считать, что атом представляет собой шар, вписанный в куб. Приравняем длину ребра куба, т. е. диаметр атома, к корню кубическому из полученного объема:
Таким образом, диаметр атома железа в кристалле приближенно равен 0,000000023 см. Это и есть межъядерное расстояние. Полученное число – не диаметр изолированного атома, т. к. электронные оболочки атомов представляют собой нечто похожее на облака с сильно размытыми краями. В строгой научной литературе по химии и физике не пользуются выражениями «диаметр атома» или «радиус атома», а применяют термин «межъядерное расстояние» и обозначение l («эль»). Почему диаметр атома железа D и его межъядерное расстояние l равны, вам станет ясно из рис. 5.6. По справочным данным радиус атома железа равен 124,1 пм = 1,24•10 –8 см, поэтому межъядерное расстояние равно 2,48•10 –8 см.
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Элемент | Радиус, см | Межъядерное расстояние, см | |
|---|---|---|---|
| Калий | К | 2,27•10 –8 | 4,54•10 –8 |
| Кальций | Са | 1,97•10 –8 | 3,94•10 –8 |
| Скандий | Sc | 1,61•10 –8 | 3,22•10 –8 |
| Титан | Ti | 1,44•10 –8 | 2,88•10 –8 |
| Ванадий | V | 1,32•10 –8 | 2,64•10 –8 |
| Хром | Cr | 1,24•10 –8 | 2,48•10 –8 |
| Марганец | Mn | 1,24•10 –8 | 2,48•10 –8 |
| Железо | Fe | 1,24•10 –8 | 2,48•10 –8 |
| Кобальт | Co | 1,25•10 –8 | 2,50•10 –8 |
| Никель | Ni | 1,24•10 –8 | 2,48•10 –8 |
| Медь | Cu | 1,28•10 –8 | 2,56•10 –8 |
| Цинк | Zn | 1,33•10 –8 | 2,66•10 –8 |
| Галлий | Ga | 1,22•10 –8 | 2,44•10 –8 |
| Германий | Ge | 1,23•10 –8 | 2,46•10 –8 |
| Мышьяк | As | 1,25•10 –8 | 2,50•10 –8 |
| Селен | Se | 2,15•10 –8 | 4,30•10 –8 |
Нарисуйте график изменения межъядерных расстояний при переходе от калия к селену. Если вам удастся объяснить ход изменения межъядерных расстояний, то вы поймете некоторые особенности построения периодической таблицы элементов Д.И.Менделеева.
Если вам в будущем придется приготовлять сплавы различных металлов, то сведения по радиусам атомов помогут вам предсказать свойства сплавов.
Сплавы металлов – твердые системы, образованные из двух и более металлов (а также металлов и неметаллов). Сплавы обладают лучшими свойствами по сравнению с составляющими их металлами. Одна из классификаций сплавов основана на числе фаз, составляющих сплав. Если в сплаве только одна фаза, то это однофазная система, или твердый раствор одного металла в другом.
Несколько слов скажем о твердых растворах. Полная взаимная растворимость металлов в любых соотношениях наблюдается редко. Такое может быть у компонентов, близких по свойствам. Например, золото и серебро могут растворяться друг в друге в любых соотношениях, т. к. они находятся в одной подгруппе и размеры их атомов близки (1,442•10 –8 и 1,444•10 –8 см соответственно).
Твердый раствор – фаза переменного состава, в которой атомы различных элементов размещены в общей кристаллической решетке. Различают твердые растворы замещения и внедрения.
Твердый раствор замещения образуется при расположении атомов растворяемого металла в заселяемых местах (узлах) решетки растворяющего металла. Радиусы атомов в таких растворах отличаются друг от друга не более чем на 15% (для сплавов железа – не более чем на 8%). Предскажите, какие твердые растворы могут быть образованы приведенными выше металлами. Другое важное требование для образования твердых растворов замещения – металлы должны быть электрохимически подобны, т. е. находиться не слишком далеко друг от друга в ряду напряжений (точнее, в ряду электродных потенциалов).
Твердый раствор внедрения образуется в результате того, что атомы растворяемого металла размещаются в пустотах между заселяемыми местами (узлами) кристаллической решетки. Размер атомов растворяемого металла не должен быть больше чем на 63% размера атома растворяющего металла.
Чем определяется межъядерное расстояние в молекулах
Основы строения вещества
Глава 9. Ковалентная связь
Первая теория ковалентной связи принадлежит американскому физикохимику Г.-Н. Льюису. В 1916 г. он предположил, что связи между двумя атомами осуществляется парой электронов, при этом вокруг каждого атома обычно формируется восьмиэлектронная оболочка (правило октета).
Для описания ковалентной связи используют преимущественно два метода, основанных на разных приближениях при решении уравнения Шредингера: метод молекулярных орбиталей и метод валентных связей. В настоящее время в теоретической химии используется почти исключительно метод молекулярных орбиталей. Однако метод валентных связей, несмотря на большую сложность вычислений, дает более наглядное представление об образовании и строении химических частиц.
Параметры ковалентной связи
Совокупность атомов, образующих химическую частицу, существенно отличается от совокупности свободных атомов. Образование химической связи приводит, в частности, к изменению радиусов атомов и их энергии. Происходит также перераспределение электронной плотности: повышается вероятность нахождения электронов в пространстве между связываемыми атомами.
Длина химической связи
r(A−B) Связь
Валентные углы
Энергия ковалентной связи
Химическое соединение образуется из отдельных атомов только в том случае, если это энергетически выгодно. Если силы притяжения преобладают над силами отталкивания, потенциальная энергия взаимодействующих атомов понижается, в противном случае − повышается. На некотором расстоянии (равном длине связи r0) эта энергия минимальна.
Таким образом, при образовании химической связи энергия выделяется, при ее разрыве − поглощается. Энергия E0, необходимая для того, чтобы разъединить атомы и удалить их друг от друга на расстояние, на котором они не взаимодействуют, называется энергией связи. Для двухатомных молекул энергия связи определяется как энергия диссоциации молекулы на атомы. Она может быть измерена экспериментально.
В молекуле водорода энергия связи численно равна энергии, которая выделяется при образовании молекулы Н2 из атомов Н:
Эту же энергию нужно затратить, чтобы разорвать связь Н-Н:
Для многоатомных молекул эта величина является условной и отвечает энергии такого процесса, при котором данная химическая связь исчезает, а все остальные остаются без изменения. При наличии нескольких одинаковых связей (например, для молекулы воды, содержащей две связи кислород−водород) их энергию можно рассчитать, используя закон Гесса. Величины энергии распада воды на простые вещества, а также энергии диссоциации водорода и кислорода на атомы известны:
Н2 = 2Н; 432 кДж/моль
О2 = 2О; 494 кДж/моль
Учитывая, что в двух молекулах воды содержится 4 связи, энергия связи кислород-водород равна:
В молекулах состава ABn последовательный отрыв атомов В сопровождается определенными (не всегда одинаковыми) затратами энергии. Например, значения энергии (кДж/моль) последовательного отщепления атомов водорода от молекулы метана существенно различаются:
| 427 | 368 | 519 | 335 | |||||
| СН4 | → | СН3 | → | СН2 | → | СН | → | С |
При этом энергия связи А−В определяется как средняя величина затраченной энергии на всех стадиях:
СН4 = С + 4Н; 1649 кДж/моль
Е(С−Н) = 1649 / 4 = 412 кДж/моль
Энергии некоторых простых и кратных связей
| Связь | Энергия (кДж/моль) | Связь | Энергия (кДж/моль) |
| С-С | 343 | С-О | 351 |
| С=С | 615 | С=О | 711 |
| С≡С | 812 | С≡O | 1096 |
Полярность ковалентной связи
Полярность химической связи зависит от разности электроотрицательностей связываемых атомов.
Электроотрицательность − условная величина, характеризующая способность атома в молекуле притягивать электроны. Если в двухатомной молекуле А−В образующие связь электроны притягиваются к атому В сильнее, чем к атому А, то атом В считается более электроотрицательным.
Шкала электроотрицательности была использована Л. Полингом для количественной характеристики способности атомов к поляризации ковалентных связей. Для количественного описания электроотрицательности, помимо термохимических данных, используют также данные о геометрии молекул (метод Сандерсона) или спектральные характеристики (метод Горди). Широко используют также шкалу Олреда и Рохова, в которой при расчете используют эффективный заряд ядра и атомный ковалентный радиус. Наиболее ясный физический смысл имеет метод, предложенный американским физикохимиком Р. Малликеном (1896-1986). Он определил электроотрицательность атома как полусумму его сродства к электрону и потенциала ионизации. Значения электроотрицательности, базирующиеся на методе Малликена и распространенные на широкий круг разнообразных объектов, называют абсолютными.
Количественной оценкой полярности («ионности») связи могут служить эффективные заряды атомов. Эффективный заряд атома характеризует разность между числом электронов, принадлежащих данному атому в химическом соединении, и числом электронов свободного атома. Атом более электроотрицательного элемента притягивает электроны сильнее. Поэтому электроны оказываются ближе к нему, и он получает некоторый отрицательный заряд, который называют и эффективным, а у его партнера появляется такой же положительный заряд. Если электроны, образующие связь между атомами, принадлежат им в равной степени, эффективные заряды равны нулю. В ионных соединениях эффективные заряды должны совпадать с зарядами ионов. А для всех других частиц они имеют промежуточные значения.
где q − заряд полюса диполя, равный для двухатомной молекулы эффективному заряду, r − межъядерное расстояние.
Дипольный момент связи является векторной величиной. Он направлен от положительно заряженной части молекулы к ее отрицательной части. На основании измерения дипольного момента было установлено, что в молекуле хлороводорода HCl на атоме водорода имеется положительный заряд +0,2 доли заряда электрона, а на атоме хлора отрицательный заряд −0,2. Значит, связь H−Cl на 20% имеет ионный характер. А связь Na−Cl является ионной на 90%.
Определение межъядерных расстояний молекулы по вращательным спектрам
Страницы работы
Содержание работы
ОПРЕДЕЛЕНИЕ МЕЖЪЯДЕРНЫХ РАССТОЯНИЙ МОЛЕКУЛЫ ПО ВРАЩАТЕЛЬНЫМ СПЕКТРАМ
Цель работы:Изучить закономерности вращательных спектров молекул, рассчитать межъядерное расстояние двухатомной молекулы на основе ее экспериментального вращательного спектра
Задание
1. Изучить принципиальную схему регистрации вращательных спектров поглощения.
2. Изучить следующие теоретические вопросы:
· Вращательная энергия и спектр двухатомной молекулы в приближении жесткого ротатора.
· Влияние нежесткости химической связи молекулы на ее вращательные постоянные и спектр.
· Расчет равновесного 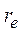
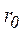
Вращательная энергия 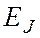
В модели жесткого ротатора имеем:
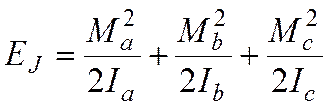
где Ма, Мb, Мc – проекции вращательного момента 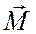
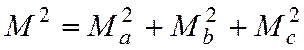
Для N – атомной молекулы имеем:
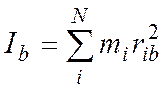
здесь ria, rib, ric – расстояние i-того атома от осей а, b, c. В этой системе справедливо:
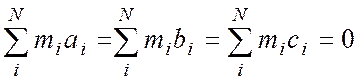
Рассмотрим двухатомную молекулу ХУ, связав с ней систему главных осей инерции (смотри рисунок).
Точка 0 помещена в центр инерции молекулы.
Тогда в соответствии с (2), видим:
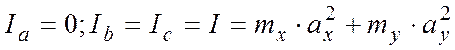
С учетом (3), а также с учетом 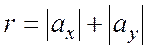
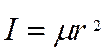
где 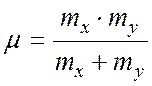
 |
Используя выражение (1), для двухатомной молекулы получим:
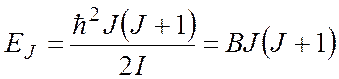
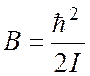
В микроволновом (МВ) спектре поглощения реализуется следующее правило обора:
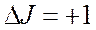
следовательно, в МВ спектре возможны переходы с частотой
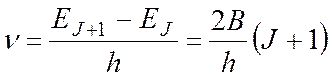
Во вращательном спектре комбинационного рассеяния (КР) реализуются следующие правила отбора:
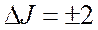
Тогда смещение линии в КР спектре определится:
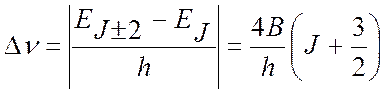
Более точной моделью для описания вращательных спектров является модель нежесткого ротатора, в которой учитывается деформация молекулы (изменение длины связей и валентных углов) в результате ее колебаний и центробежного растяжения.
Влияние колебаний на вращательную энергию молекулы может быть внесено в виде поправки во вращательную постоянную. Для двухатомной молекулы вращательная постоянная Вυ для данного υ-го колебательного состояния имеет вид
где Ве – эффективное значение вращательной постоянной, постоянное для всех υ данной молекулы; αе – постоянная колебательно-вращательного взаимодействия; υ – колебательное квантовое число.
Таким образом, с учетом колебаний в формулах (5), (7), (8) необходимо использовать 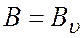
Влияние центробежного растяжения, усиливающегося с ростом j, учитывается следующим образом:
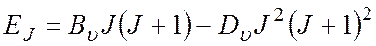
где 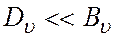
Тогда выражение для частот спектральных линий в спектре ИК-поглощения (7) и в спектре комбинационного рассеяния (8) примут вид:
Проанализировав ИК либо КР спектры и определив ν либо Δν, находим Вυ и Dυ. Воспользовавшись формулами (4), (6) и полученными значениями Вυ, рассчитаем 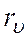
Формула (9) позволяет на основе измеренных значений Вυ получить значения Ве и αе, что, в свою очередь, дает возможность с помощью формул (4), (6) найти значение re.
В микроволновом спектре поглощения паров фторида лития ( 6 LiF) измерены следующие линии поглощения, отнесенные к колебательным состояниям υ = 0, 1, 2 и 3.
переход

 = 7,87 г/см 3 ). Вычислим объем 1 моль железа:
= 7,87 г/см 3 ). Вычислим объем 1 моль железа: