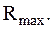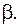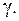Чем определяется максимально возможная пропускная способность идеального канала связи

Пропускная способность СПИ.

Пропускная способность системы связи – это максимально-возможная (предельная) скорость передачи информации (при условии, что канал не вносит ошибок и искажений) –

Пропускную способность системы передачи аналоговых сообщений оценивают количеством одновременно передаваемых телефонных разговоров, радиовещательных или ТВ программ и т. п.

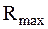
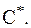
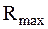
Пропускную способность системы не следует путать с пропускной способностью канала связи Она характеризует максимальное количество информации, которое может быть передано по данному каналу в единицу времени. В реальных системах скорость передачи всегда меньшепропускной способности канала

В теории информации доказывается, что при 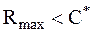существуют такие способы передачи и соответствующие способы приёма, при которых верность передачи может быть сделана сколь угодно большой. Пропускная способность системы связи – понятие техническое, характеризующее используемую аппаратуру, тогда как пропускная способность канала является фундаментальным теоретическим понятием, определяющим потенциальные возможности системы связи, использующей данный канал.

Работа любой технической системы оценивается эффективностью. В свою очередь эффективность любой технической системы определяется количеством и качеством выдаваемой продукции. В системах связи такой продукцией является передаваемая информация, количество которой определяется: средней скоростью передачи, а качество – величиной ошибки.

Важнейшими показателями эффективности систем связи являются:

1. Информационная эффективность 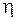– определяет степень использования системой связи пропускной способности канала.

2. Степень использования канала по мощности

3. Степень использования канала по частоте

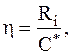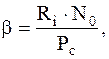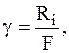			(1.9)
где		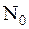–	мощности шума;
F	–	ширина полосы пропускания;
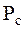	–	мощность сигнала.

Шеннон показал, что пропускная способность канала с аддитивным белым гауссовским шумом является функцией средней мощности принятого сигнала S, средней мощности шума N и ширины полосы пропускания F. Выражение для пропускной способности канала связи(теорема Шеннона- Хартли) можно записать следующим образом:

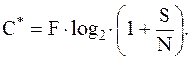(1.10)

Если F измеряется в герцах, а логарифм берётся по основанию 2, то пропускная способность будет иметь размерность бит / c. Теоретически информацию можно по каналу передавать со сколь угодно малой вероятности ошибки с любой скоростью 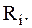В работе Шеннона показано, что величины S, N, F устанавливают пределы скорости передачи, а не вероятности появления ошибок.

В современных цифровых системах связи используется термин: скорость передачи данных – это величина (бит/с) определяется с помощью формулы (1.7).

Важной характеристикой системы является своевременность, которая определяется допустимой задержкой, обусловленной преобразованием сообщений и сигналов, а также конечным временем распространения сигнала по каналу связи. Она зависит, во-первых, от характера и протяжённости канала, во-вторых, от длительности обработки сигнала в приёмном и передающем устройствах. Скорость передачи и задержка являются независимыми характеристиками, практически не связанными друг с другом.

Существуют и многие другие параметры характеризующие с различных точек зрения качества системы связи. К ним относятся скрытность связи, надёжность системы, габаритные размеры и масса аппаратуры и т.д., которые не рассматриваются в курсе ТЭС. Им посвящены отдельные разделы других специальных курсов.

1. Пропускная способность СПИ – это максимально-возможная (предельная) скорость передачи информации (при условии, что канал не вносит ошибок и искажений) –

2. В реальных системах скорость передачи 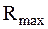всегда меньше пропускной способности канала

1. Важнейшими характеристиками системы связи являются верность и скорость передачи сообщений. Первая определяет качество передачи, а второе – количество. При передаче дискретных сообщений верность (помехоустойчивость) определяется вероятностью ошибки, а при передаче непрерывных сообщений – среднеквадратической ошибкой. Скорость измеряется чаще всего числом передаваемых двоичных единиц информации в единицу времени (бит/с).

Литература

1. Теория электрической связи: Учеб. Для вузов / А.Г. Зюко, Д. Д. Кловский, В.И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М.: Радио и связь, 1998. – 433 с.

1. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.

2. Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.

3. Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.

4. Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.

Источник

Национальная библиотека им. Н. Э. Баумана
Bauman National Library

Персональные инструменты

Пропускная способность каналов передачи сообщений

Содержание

Общие положения

Пропускная способность системы передачи или извлечения информации соответственно характеризует максимально допускаемую этой системой скорость передачи или извлечения информации с заданной степенью достоверности (точности). Для количественной характеристики пропускной способности применяются различные показатели в зависимости от вида и назначения системы. Так, если СПИ содержит один канал или несколько однородных каналов (например, только телефонные каналы), то ее пропускную способность удобно оценивать в битах в секунду. Если же СПИ содержит разнородные каналы (например, телефонные и телевизионные), то в общем случае объединять потоки передаваемой по ним качественно различной информации в один общий поток недопустимо и приходится оценивать пропускную способность системы в целом не одним числом, а несколькими числами — отдельно для каждой группы каналов. При этом можно оценивать пропускную способность системы числами каналов каждого вида. Однако в ряде случаев потоки на выходах всех разнородных каналов имеют цифровой код в двоичной системе исчисления и суммируются в общий цифровой поток двоичных символов для последующей обработки в ЭВМ, и/или последующей передачи, осуществляемой другой системой. В таких случаях полезно оценивать пропускную способность системы в целом также одним числом, измеряемым в битах в секунду.

Аналогичная ситуация имеет место и в системах извлечения информации (СИИ). В ряде случаев СИИ, например радиолокатор, имеет несколько каналов, извлекающих качественно различные виды информации (о наличии или отсутствии целей, о числе и типах целей, их координатах, скоростях и т.п.). При этом суммировать все качественно различные виды информации в один общий поток и измерять его в битах в общем случае недопустимо — приходится оценивать пропускную способность СИИ другим способом, например числом целей данного вида, обслуживаемых в единицу времени или одновременно. Однако если потоки информации на выходе всех каналов СИИ имеют цифровой вид и объединяются в единый двоичный цифровой поток для последующего ввода в ЭВМ и/или дальнейшей передачи информации, то целесообразно характеризовать суммарную пропускную способность СИИ не только числом обслуживаемых целей, но и показателем, выраженным в битах в секунду.

Таким образом, в зависимости от характера и назначения си¬стемы ее пропускную способность можно оценивать одним или несколькими показателями и измерять в битах в секунду или в других единицах. В дальнейшем будем для простоты рассматривать лишь первый случай. При этом под пропускной способностью C <\displaystyle

C> системы (СПИ или СИИ) понимается максимальное (по всем возможным источникам И информации) значение средней скорости R <\displaystyle

R> передачи или извлечения информации, допускаемое этой системой при заданных требованиях к достоверности (точности) передачи (извлечения) информации:

J_T> — среднее количество информации (в битах), передаваемой или извлекаемой системой за время T <\displaystyle

\varepsilon > — показатель достоверности (точности) передачи (извлечения) информации (Р_ошибки, δ 2 <\displaystyle

\delta_2> и т.п.). В процессе проектирования приходится сравнивать различные варианты S <\displaystyle

S> построения системы и выбирать наилучший из некоторого множества M S <\displaystyle

M_S> допустимых вариантов. Поэтому представляет интерес определение максимального значения C m a x <\displaystyle

C_> пропускной способности, являющегося решением задачи

При этом в процессе отыскания максимума величины C <\displaystyle

C> может варьироваться не только структура системы, но и значения ее параметров. Чем шире множество M S <\displaystyle

C_> То предельное значение величины C m a x <\displaystyle

C_> (а значит, и величины C <\displaystyle

C> ), которое может быть достигнуто при весьма слабых ограничениях, будем называть потенциальной (предельной теоретически достижимой) пропускной способностью и обозначать C 0 <\displaystyle

M_> — достаточно широкое множество (класс) рассматриваемых вариантов S <\displaystyle

S> построения системы.

Очевидно, величина C 0 <\displaystyle

C_0> будет зависеть от того, что конкретно будет пониматься под «достаточно широким множеством M S 0 <\displaystyle

M_> » или соответственно под «достаточно слабыми ограничениями вариантов S <\displaystyle

S> построения системы». Поэтому потенциальная пропускная способность системы, равно как и другие потенциальные характеристики (например, потенциальная помехоустойчивость), существенно зависит от исходных данных, принятых при ее определении. При определении пропускной способности ( C <\displaystyle

C_0> ) в общем случае следует учитывать действие помех и других источников ошибок. Поэтому между показателями пропускной способности, точности и помехоустойчивости существует взаимная связь — пропускная способность ( C <\displaystyle

C_0> ) зависит, как правило, от допустимых значений показателей точности и помехоустойчивости.

Определение пропускной способности КПС в классической теории информации

Классическая теория информации, основы которой были заложены К. Шенноном, обычно изучается в курсе «Системы передачи информации». Мы рассмотрим лишь основные результаты этой теории, необходимые для понимания последующего материала.

Система передачи информации полагается состоящей из трех частей (рис. 1) — канала связи, а также кодера и декодера,

согласующих канал с источником информации И и ее получателем (адресатом) П. В частном случае кодер и декодер могут отсутствовать. Канал может быть дискретным или непрерывным, а источник И может выдавать на своем выходе дискретные или непрерывные сообщения.

Передача дискретных сообщений по дискретному каналу. При этом источник вырабатывает информацию со средней скоростью

V_i> — средняя скорость выработки символов источником;

H_i (x_i)> — среднее количество информации в битах, приходящееся на один символ, называемое также энтропией или неопределенностью источника’.

H_> — число видов символов источника; P ( x i ) <\displaystyle

P(x_i)> — вероятность появления символа x i <\displaystyle

Если между символами источника имеется статистическая связь, то H i ( x i ) <\displaystyle

В отсутствие шумов дискретный канал характеризуется числом n k <\displaystyle

n_k> видов передаваемых им символов и допустимой средней скоростью V k <\displaystyle

V_k> следования этих символов.

Так как источники искажений в кодере, декодере и канале полагаются отсутствующими, то информация передается без искажений, т.е. H i ( x i ) <\displaystyle

H_> следует понимать значения соответствующих параметров на выходе кодера.

Как доказал К. Шеннон, если производительность источника И не превышает С, осуществить такое кодирование символов источника в принципе всегда возможно. При этом источник должен вырабатывать символы со скоростью V i = C i <\displaystyle

При наличии помех дискретный канал характеризуется не только параметрами n k <\displaystyle

V_i> на входе канала в символ x j <\displaystyle

x_j> на его выходе. При этом символ x j <\displaystyle

x_j> обозначается здесь через y j <\displaystyle

y_j> для того, чтобы подчеркнуть, что он появляется на выходе канала, т.е. в составе процесса y ( t ) <\displaystyle

и характеризующая уменьшение скорости передачи информации за счет действия помех в канале [в отсутствие помех H ( x | y ) = 0 <\displaystyle

x_j> (а также между символами y j <\displaystyle

y_j> ) с различными индексами отсутствует.

P_ \to 0> ), если выполняется условие R i ≤ C <\displaystyle

R_i \le C > и осуществляется идеальное кодирование (и декодирование) информации, поступающей от источника И. Идеальное кодирование (и декодирование) предполагает совместную обработку последовательности сколь угодно большого числа символов и соответственно требует неограниченно большой задержки t 3 <\displaystyle

t_3> в передаче информации ( t 3 → 1 <\displaystyle

Частным, но весьма важным случаем дискретного канала является двоичный симметричный канал без памяти, т.е. канал, в котором n k = 2 <\displaystyle

Благодаря наличию идеального кодирования и декодирования вероятность P o s h <\displaystyle

P_ \to 5> пропускная способность C <\displaystyle

т.е. при этом пропускная способность уменьшается за счет действия помех менее чем на 10%.

Передача дискретных сообщений по непрерывному каналу

Непрерывным называется канал, способный передавать сигналы, непрерывные как по времени, так и по значениям в каждый момент времени. Полагается, что передаваемые по каналу сигналы имеют спектр, ширина которого равна полосе пропускания △ f <\displaystyle

\vartriangle f> канала и длительность T <\displaystyle

u(t)> полностью характеризуются своими отсчетами, взятыми в дискретные моменты времени с временным интервалом △ t / 1 2 △ f <\displaystyle

Значение каждого отсчета непрерывно, т.е. может иметь бесконечное число (точнее — континуум) значений даже в пределах сколь угодно малого интервала △ u <\displaystyle

\vartriangle u > этих значений. Поэтому непрерывный канал можно рассматривать как предел дискретного канала, в котором роль передаваемых символов играют отсчеты, а число n k <\displaystyle

n_k> возможных видов (значений) этих символов стремится к бесконечности. Отсюда следует, что все соотношения, полученные для дискретного канала, остаются справедливыми и для непрерывного канала, если в них положить V k = 2 △ f <\displaystyle

V_k = 2 \vartriangle f > и n k → 1 <\displaystyle

— так называемые дифференциальные энтропии, a W ( x ) <\displaystyle

W(x|y)> — безусловная и условная плотность вероятности величины x <\displaystyle

Если дисперсия Φ x 2 <\displaystyle

x > фиксирована, то максимум энтропии h ( x ) <\displaystyle

h(x) > имеет место при нормальном (гауссовском) законе распределения W ( x ) <\displaystyle

Если единственным источником искажений в канале является аддитивный независимый нормальный белый шум со спектральной плотностью N 0 <\displaystyle

P_c> — средняя мощность сигнала.

N0> и задана лишь средняя мощность где P c <\displaystyle

Чем меньше каждая из величин (где β E <\displaystyle

\beta_<\vartriangle f>> ), тем лучше система при прочих равных условиях. Поэтому удельные расходы ( β E <\displaystyle

Поскольку, как уже отмечалось, непрерывный канал можно рассматривать как предел дискретного канала, имеющий место при n k → 1 <\displaystyle

n_k> пропускная способность дискретного канала возрастает, справедливо следующее утверждение: если в дискретном канале с полосой пропускания △ f <\displaystyle

\vartriangle f> единственным источником искажений сообщений является аддитивный независимый нормальный белый шум со спектральной плоскостью N 0 <\displaystyle

N0> и ограничена (значением P c <\displaystyle

P_c> ) лишь средняя мощность сигнала, то при увеличении числа n k <\displaystyle

n_k> видов символов пропускная способность канала возрастает, стремясь в пределе (при n k → 1 <\displaystyle

n_k = 2> ) проигрыш в величине C <\displaystyle

C> (по сравнению со случаем n k → 1 <\displaystyle

n_k \to \mathcal<1>> ) получается сравнительно небольшим, если полоса пропускания канала относительно велика ( △ f ≫ C <\displaystyle

\vartriangle f \gg C> ). В общем случае, т.е. при произвольном отношении β △ f = 1 / C <\displaystyle

Из рис. 2 видно, что при β △ f > 0.6 <\displaystyle

n_k> в требуемой средней мощности сигнала в двоичном канале по сравнению с непрерывным невелик: n k 2 <\displaystyle

Соответствующие зависимости β E = f ( β △ f ) <\displaystyle

\beta_ <\Epsilon>= f( \beta_<\vartriangle f>)> для дискретных каналов с большим числом видов символов ( n k > 2 <\displaystyle

n_k > 2> ) должны располагаться между штриховой и сплошной линиями, стремясь при n k → 1 <\displaystyle

n_k \to \mathcal<1>> к сплошной линии. Отсюда следует, что основным преимуществом непрерывного канала по сравнению с дискретным является возможность существенного уменьшения удельного расхода средней мощности при малых значениях удельного расхода полосы ( P △ f 0.5 <\displaystyle

P_ \to 0> ), если применить идеальное помехоустойчивое кодирование, основанное на преобразовании входной последовательности x i ( t ) <\displaystyle

x_i(t)> символов в весьма длительные ( T → 1 <\displaystyle

T \to \mathcal<1>> ) реализации x ( t ) <\displaystyle

x(t)> передаваемого по каналу сообщения и соответственно требующее весьма большой задержки ( t 3 → 1 <\displaystyle

t_3 \to \mathcal<1>> ) в передаче информации от источника к потребителю.

Передача непрерывных сообщений

x_i(t)> имеет спектр, ограниченный высшей частотой F B <\displaystyle

R_i \to \mathcal<1>> ). Пропускная же способность непрерывного канала при наличии шумов конечна. Поэтому передавать сообщение такого источника по каналу с шумами со сколь угодно высокой точностью невозможно даже при наличии идеального помехоустойчивого кодирования (и декодирования).

К. Шеннон доказал, что при наличии идеального помехоустойчивого кодирования (и декодирования) можно обеспечить передачу непрерывных сообщений по каналу с пропускной способностью C <\displaystyle

C> лишь с относительным средним квадратом ошибки δ 2 <\displaystyle

Здесь по определению

\epsilon > ошибки передачи сообщений, отнесенный к среднему квадрату передаваемого сообщения. Величина R i ϵ <\displaystyle

R_ > называется ε-производительностью источника, чтобы подчеркнуть, что она соответствует точной (с P o s h → 0 <\displaystyle

P_ \to 0> ) передаче по каналу не истинного сообщения x i ( t ) <\displaystyle

x_i(t)> источника, а сообщения y ( t ) <\displaystyle

x_i(t)> на величину ( y − x i <\displaystyle

y-x_i> ), средний квадрат которой равен заданной (достаточно малой) величине ϵ <\displaystyle

x_i> имеет нормальный закон распределения и равномерный в пределах полосы [0, F B <\displaystyle

F_B> ] и равный нулю за ее пределами, возможно передавать сообщение по каналу с относительным средним квадратом ошибки δ 2 <\displaystyle

C> была бесконечно большой, то при идеальном кодировании можно было бы передавать сообщение x i ( t ) <\displaystyle

x_i(t)> практически безошибочно ( δ 2 → 0 <\displaystyle

P_ \to 0> ). При конечной пропускной способности канала обеспечить такой результат невозможно даже при идеальном кодировании — чем меньше пропускная способность C <\displaystyle

C> канала, тем с большим средним квадратом ошибки возможно передавать по нему сообщения. Понятно также, что при этом должно играть роль не абсолютное значение пропускной способности, а ее отношение к высшей частоте F B <\displaystyle

F_B> в спектре сообщения.

Отсюда следует, что при P c / N 0 → 1 <\displaystyle

P_c / N0 > ошибка δ 2 <\displaystyle

\delta^2> монотонно возрастает.

Если источник при данной ошибке δ 2 <\displaystyle

\delta^2> имеет производи тельность R i ϵ <\displaystyle

то можно в принципе закодировать сообщения на выходе источника и передавать их по каналу с пропускной способностью C <\displaystyle

C> при погрешности воспроизведения, как угодно близкой к δ 2 <\displaystyle

R_ . Это невозможно, если R i ϵ > C <\displaystyle

R_ > C > (теорема Шеннона для непрерывного источника).

Источник