Чем обычно характеризуется эллипсоид

Эллипсоид

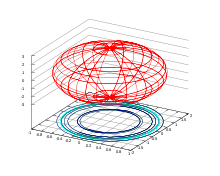
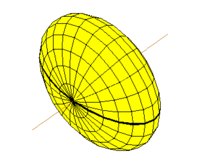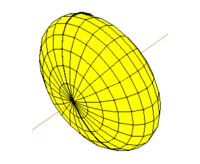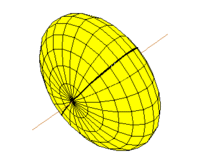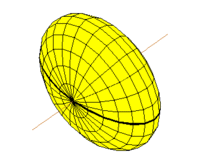
Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:

где — произвольные положительные числа.

Величины a, b, c называют полуосями эллипсоида. Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.

В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом.

Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли.

Площадь поверхности эллипсоида вращения:

Литература

Полезное

Смотреть что такое «Эллипсоид» в других словарях:

Эллипсоид — Эллипсоид. ЭЛЛИПСОИД, поверхность, которую можно получить из сферы, если сферу сжать (растянуть) в произвольных отношениях в трех взаимно перпендикулярных направлениях. Если эллипс вращать вокруг одной из его осей, то описываемая им поверхность… … Иллюстрированный энциклопедический словарь

ЭЛЛИПСОИД — (греч., от elleipsis эллипсис, и eidos сходство). Геометрическое тело, происходящее от обращения полуэллипса вокруг одной из своих осей. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЭЛЛИПСОИД греч., от elleipsis … Словарь иностранных слов русского языка

эллипсоид — а, м. ellipsoïde m. спец. Поверхность, образуемая вращением эллипса вокруг одной из своих осей. БАС 1. Глобусы в виде шара, груши, элипсоида. Кукольник Примеч. // К. 1851 1 556. Гало. Это эллипсоид диаметром более 600 тысяч световых лет,… … Исторический словарь галлицизмов русского языка

Эллипсоид — земной (a. earth ellipsoid; н. Erdellipsoid; ф. ellipsoide terrestre; и. elipsoide terrestre) эллипсоид вращения, наилучшим образом представляющий фигуру Геоида. Eго размеры и положение в теле Земли определяют из градусных измерений,… … Геологическая энциклопедия

эллипсоид — сущ., кол во синонимов: 5 • безгранник (2) • коноид (4) • референц эллипсоид (2) … Словарь синонимов

ЭЛЛИПСОИД — ЭЛЛИПСОИД, эллипсоида, муж. (мат.). Яйцевидное шарообразное тело, получающееся при вращении эллипса вокруг одной из своих осей. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

эллипсоид — а; м. [от греч. elleipsis выпадение, опущение и eidos вид] Матем. Поверхность, образуемая вращением эллипса (1.Э.; 1 зн.) вокруг одной из своих осей. ◁ Эллипсоидный, ая, ое. * * * эллипсоид замкнутая поверхность (2 го порядка). Эллипсоид можно… … Энциклопедический словарь

Эллипсоид — [ellipsoid] замкнутая центральная поверхность 2 го порядка. Эллипсоид имеет центр симметрии и три оси симметрии, которые называются осями эллипсоида: Смотри также: эллипсоид деформации эллипсоид напряжений … Энциклопедический словарь по металлургии

эллипсоид — 3.43 эллипсоид: Поверхность, полученная при вращении эллипсоида вокруг собственной оси. Примечание Параметры каждого эллипсоида определяются измерениями формы и размеров Земли, чтобы аппроксимировать геоид с наиболее возможно высокой точностью.… … Словарь-справочник терминов нормативно-технической документации

ЭЛЛИПСОИД — (от эллипс и греч. eidos вид) поверхность 2 го порядка. Может быть получена из поверхности шара, если шар сжать (растянуть) в произвольных отношениях в трёх взаимно перпендикулярных направлениях х, у, z (см. рис.). Если эллипс вращать вокруг… … Большой энциклопедический политехнический словарь

Источник

СОДЕРЖАНИЕ

Стандартное уравнение

Используя декартову систему координат, в которой начало координат является центром эллипсоида, а оси координат являются осями эллипсоида, неявное уравнение эллипсоида имеет стандартную форму

Параметризация

Эллипсоид можно параметризовать несколькими способами, которые проще выразить, когда оси эллипсоида совпадают с осями координат. Обычный выбор

Измерение от центра, а не от полюса,

Измерение углов непосредственно к поверхности эллипсоида, а не к описанной сфере,

Объем

Это уравнение сводится к уравнению объема сферы, когда все три эллиптических радиуса равны, и к уравнению сплющенного или вытянутого сфероида, когда два из них равны.

Площадь поверхности

Площадь поверхности общего (трехосного) эллипсоида равна

Площадь поверхности эллипсоида вращения (или сфероида) может быть выражена через элементарные функции :

Примерная формула

Здесь p ≈ 1,6075 дает относительную ошибку не более 1,061%; значение p = 8 / 5 = 1,6 оптимально для эллипсоидов, близких к сферической, с относительной погрешностью не более 1,178%.

Плоские секции

Характеристики

Пересечение плоскости и сферы представляет собой окружность (либо сводится к одной точке, либо пусто). Любой эллипсоид является изображением единичной сферы при некотором аффинном преобразовании, а любая плоскость является изображением некоторой другой плоскости при таком же преобразовании. Итак, поскольку аффинные преобразования преобразуют круги в эллипсы, пересечение плоскости с эллипсоидом является эллипсом, единственной точкой или пусто. Очевидно, что сфероиды содержат круги. Это также верно, но менее очевидно, для трехосных эллипсоидов (см. Круглый раздел ).

Определение эллипса плоского сечения

его единичный вектор нормали. Следовательно

является центром пересечений окружности и

его радиус (см. диаграмму).

Если m _w = ± 1 (т. Е. Плоскость горизонтальна), пусть

Штифтовая конструкция

Построение «кегли и струны» эллипсоида вращения дается конструкцией вращающегося эллипса «кегли».

Построение точек трехосного эллипсоида сложнее. Первые идеи принадлежат шотландскому физику Дж. К. Максвеллу (1868 г.). Основные исследования и распространение на квадрики были выполнены немецким математиком О. Штауде в 1882, 1886 и 1898 годах. Описание конструкции эллипсоидов и гиперболоидов с помощью булавок и струн содержится в книге « Геометрия и воображение», написанной Д. Гильберт и С. Фоссен тоже.

Этапы строительства

с вершинами и фокусами эллипса

Полуоси

Уравнения для полуосей сгенерированного эллипсоида могут быть получены путем специального выбора для точки P :

Converse

Конфокальные эллипсоиды

Если Е представляет собой эллипсоид конфокальный к Е с квадратами его полуосей

Верно и обратное утверждение: если выбрать вторую строку длины l и определить

действительны, что означает, что два эллипсоида конфокальны.

Предельный случай, эллипсоид вращения

Свойства фокальной гиперболы

Свойство фокального эллипса

В общем положении

Как квадрика

Параметрическое представление

Ключом к параметрическому представлению эллипсоида в общем положении является альтернативное определение:

Аффинное преобразование может быть представлено в виде перевода с вектором ф ₀ и регулярным 3 × 3 матрицы A :

Параметрическое представление эллипсоида общего положения может быть получено с помощью параметрического представления единичной сферы (см. Выше) и аффинного преобразования:

Приложения

Эллипсоидальная форма находит множество практических применений:

Динамические свойства

Масса эллипсоида равномерной плотности р является

В моменты инерции эллипсоида однородной плотности являются

При a = b = c эти моменты инерции сводятся к моментам инерции для сферы однородной плотности.

Эллипсоиды и кубоиды стабильно вращаются вдоль своей большой или малой оси, но не вдоль средней оси. Это можно увидеть экспериментально, бросив ластик с некоторым вращением. Кроме того, соображения момента инерции означают, что вращение вдоль большой оси более легко нарушить, чем вращение вдоль малой оси.

Одним из практических последствий этого является то, что разносторонние астрономические тела, такие как Хаумеа, обычно вращаются вдоль своих малых осей (как и Земля, которая просто сплюснута ); кроме того, из-за приливной блокировки спутники находятся на синхронной орбите, такие как орбита Мимаса, с их большой осью, выровненной радиально по отношению к их планете.

Вращающееся тело из однородной самогравитирующей жидкости примет форму сфероида Маклорена (сплюснутый сфероид) или эллипсоида Якоби (разносторонний эллипсоид), когда оно находится в гидростатическом равновесии и при умеренных скоростях вращения. При более быстром вращении можно ожидать неэллипсоидальных грушевидных или яйцевидных форм, но они нестабильны.

Динамика жидкостей

По вероятности и статистике

Таким образом, функция плотности представляет собой скалярное преобразование квадратичного выражения в скалярное преобразование. Более того, уравнение для любой поверхности изоплотности утверждает, что выражение квадрики равно некоторой константе, специфичной для этого значения плотности, а поверхность изоплотности является эллипсоидом.

В высших измерениях

Источник

СОДЕРЖАНИЕ

Стандартное уравнение

Используя декартову систему координат, в которой начало координат является центром эллипсоида, а оси координат являются осями эллипсоида, неявное уравнение эллипсоида имеет стандартную форму

Параметризация

Эллипсоид можно параметризовать несколькими способами, которые проще выразить, когда оси эллипсоида совпадают с осями координат. Обычный выбор

Измерение от центра, а не от полюса,

Измерение углов непосредственно к поверхности эллипсоида, а не к описанной сфере,

Объем

Это уравнение сводится к уравнению объема сферы, когда все три эллиптических радиуса равны, и к уравнению сплющенного или вытянутого сфероида, когда два из них равны.

Площадь поверхности

Площадь поверхности общего (трехосного) эллипсоида равна

Площадь поверхности эллипсоида вращения (или сфероида) может быть выражена через элементарные функции :

Примерная формула

Здесь p ≈ 1,6075 дает относительную ошибку не более 1,061%; значение p = 8 / 5 = 1,6 оптимально для эллипсоидов, близких к сферической, с относительной погрешностью не более 1,178%.

Плоские секции

Характеристики

Пересечение плоскости и сферы представляет собой окружность (либо сводится к одной точке, либо пусто). Любой эллипсоид является изображением единичной сферы при некотором аффинном преобразовании, а любая плоскость является изображением некоторой другой плоскости при таком же преобразовании. Итак, поскольку аффинные преобразования преобразуют круги в эллипсы, пересечение плоскости с эллипсоидом является эллипсом, единственной точкой или пусто. Очевидно, что сфероиды содержат круги. Это также верно, но менее очевидно, для трехосных эллипсоидов (см. Круглый раздел ).

Определение эллипса плоского сечения

его единичный вектор нормали. Следовательно

является центром пересечений окружности и

его радиус (см. диаграмму).

Если m _w = ± 1 (т. Е. Плоскость горизонтальна), пусть

Штифтовая конструкция

Построение «кегли и струны» эллипсоида вращения дается конструкцией вращающегося эллипса «кегли».

Построение точек трехосного эллипсоида сложнее. Первые идеи принадлежат шотландскому физику Дж. К. Максвеллу (1868 г.). Основные исследования и распространение на квадрики были выполнены немецким математиком О. Штауде в 1882, 1886 и 1898 годах. Описание конструкции эллипсоидов и гиперболоидов с помощью булавок и струн содержится в книге « Геометрия и воображение», написанной Д. Гильберт и С. Фоссен тоже.

Этапы строительства

с вершинами и фокусами эллипса

Полуоси

Уравнения для полуосей сгенерированного эллипсоида могут быть получены путем специального выбора для точки P :

Converse

Конфокальные эллипсоиды

Если Е представляет собой эллипсоид конфокальный к Е с квадратами его полуосей

Верно и обратное утверждение: если выбрать вторую строку длины l и определить

действительны, что означает, что два эллипсоида конфокальны.

Предельный случай, эллипсоид вращения

Свойства фокальной гиперболы

Свойство фокального эллипса

В общем положении

Как квадрика

Параметрическое представление

Ключом к параметрическому представлению эллипсоида в общем положении является альтернативное определение:

Аффинное преобразование может быть представлено в виде перевода с вектором ф ₀ и регулярным 3 × 3 матрицы A :

Параметрическое представление эллипсоида общего положения может быть получено с помощью параметрического представления единичной сферы (см. Выше) и аффинного преобразования:

Приложения

Эллипсоидальная форма находит множество практических применений:

Динамические свойства

Масса эллипсоида равномерной плотности р является

В моменты инерции эллипсоида однородной плотности являются

При a = b = c эти моменты инерции сводятся к моментам инерции для сферы однородной плотности.

Эллипсоиды и кубоиды стабильно вращаются вдоль своей большой или малой оси, но не вдоль средней оси. Это можно увидеть экспериментально, бросив ластик с некоторым вращением. Кроме того, соображения момента инерции означают, что вращение вдоль большой оси более легко нарушить, чем вращение вдоль малой оси.

Одним из практических последствий этого является то, что разносторонние астрономические тела, такие как Хаумеа, обычно вращаются вдоль своих малых осей (как и Земля, которая просто сплюснута ); кроме того, из-за приливной блокировки спутники находятся на синхронной орбите, такие как орбита Мимаса, с их большой осью, выровненной радиально по отношению к их планете.

Вращающееся тело из однородной самогравитирующей жидкости примет форму сфероида Маклорена (сплюснутый сфероид) или эллипсоида Якоби (разносторонний эллипсоид), когда оно находится в гидростатическом равновесии и при умеренных скоростях вращения. При более быстром вращении можно ожидать неэллипсоидальных грушевидных или яйцевидных форм, но они нестабильны.

Динамика жидкостей

По вероятности и статистике

Таким образом, функция плотности представляет собой скалярное преобразование квадратичного выражения в скалярное преобразование. Более того, уравнение для любой поверхности изоплотности утверждает, что выражение квадрики равно некоторой константе, специфичной для этого значения плотности, а поверхность изоплотности является эллипсоидом.

В высших измерениях

Источник

Эллипсоид

Содержание

Стандартное уравнение [ править ]

Используя декартову систему координат, в которой начало координат является центром эллипсоида, а оси координат являются осями эллипсоида, неявное уравнение эллипсоида имеет стандартную форму

Параметризация [ править ]

Эллипсоид можно параметризовать несколькими способами, которые проще выразить, если оси эллипсоида совпадают с осями координат. Обычный выбор

Измерение от центра, а не от полюса,

Измерение углов непосредственно к поверхности эллипсоида, а не к описанной сфере,

[ x y z ] = R [ cos ⁡ ( γ ) cos ⁡ ( λ ) cos ⁡ ( γ ) sin ⁡ ( λ ) sin ⁡ ( γ ) ] <\displaystyle <\beginx\\y\\z\end>=R<\begin\cos(\gamma )\cos(\lambda )\\\cos(\gamma )\sin(\lambda )\\\sin(\gamma )\end>\,\!>

Объем и площадь [ править ]

Объем [ править ]

Обратите внимание, что это уравнение сводится к уравнению объема сферы, когда все три эллиптических радиуса равны, и к уравнению сплющенного или вытянутого сфероида, когда два из них равны.

В объемах этих вписанные и разграниченные коробки соответственно:

Площадь [ править ]

Площадь поверхности обычного (трехосного) эллипсоида равна [2] [3]

Площадь поверхности эллипсоида вращения (или сфероида) может быть выражена через элементарные функции :

S oblate = 2 π a 2 ( 1 + 1 − e 2 e artanh ⁡ e ) <\displaystyle S_<\text>=2\pi a^<2>\left(1+<\frac <1-e^<2>>>\operatorname e\right)>

S oblate = 2 π a 2 + π c 2 e ln ⁡ 1 + e 1 − e <\displaystyle S_<\text>=2\pi a^<2>\ +<\frac <\pi c^<2>>>\ln <\frac <1+e><1-e>>>

Примерная формула [ править ]

Здесь p ≈ 1,6075 дает относительную ошибку не более 1,061%; [6] значение p = 8 / 5 = 1,6 оптимально для эллипсоидов, близких к сферической, с относительной погрешностью не более 1,178%.

Сечения самолета [ править ]

Свойства [ править ]

Определение эллипса плоского сечения [ править ]

x → = f → 0 + f → 1 cos ⁡ t + f → 2 sin ⁡ t <\displaystyle <\vec >=<\vec >_<0>+<\vec >_<1>\cos t+<\vec >_<2>\sin t\quad > (см. эллипс ).

Конструкция булавок и ниток [ править ]

Построение стержней и струн эллипсоида вращения дается конструкцией вращающегося эллипса стержнями и струнами.

Этапы строительства [ править ]

с вершинами и фокусами эллипса

Полуоси [ править ]

Converse [ править ]

Конфокальные эллипсоиды [ править ]

Предельный случай, эллипсоид вращения [ править ]

Свойства фокальной гиперболы [ править ]

Свойство фокального эллипса [ править ]

В общем положении [ править ]

Как квадрик [ править ]

В более общем смысле, произвольно ориентированный эллипсоид с центром в точке v определяется решениями x уравнения

Параметрическое представление [ править ]

Ключом к параметрическому представлению эллипсоида в общем положении является альтернативное определение:

x → ↦ f → 0 + A x → = f → 0 + x f → 1 + y f → 2 + z f → 3 <\displaystyle <\vec >\mapsto <\vec >_<0>+A<\vec >=<\vec >_<0>+x<\vec >_<1>+y<\vec >_<2>+z<\vec >_<3>> ,

Параметрическое представление эллипсоида общего положения можно получить с помощью параметрического представления единичной сферы (см. Выше) и аффинного преобразования:

Приложения [ править ]

Эллипсоидальная форма находит множество практических применений:

Динамические свойства [ править ]

Масса эллипсоида равномерной плотностью р:

В моменты инерции эллипсоида однородной плотности являются:

Эллипсоиды и кубоиды стабильно вращаются вдоль своей большой или малой оси, но не вдоль средней оси. Это можно увидеть экспериментально, бросив ластик с некоторым вращением. Кроме того, соображения момента инерции означают, что вращение вдоль большой оси более легко нарушить, чем вращение вдоль малой оси. [20]

Одним из практических последствий этого является то, что разносторонние астрономические тела, такие как Хаумеа, обычно вращаются вдоль своих малых осей (как и Земля, которая просто сплюснута); кроме того, из-за приливной блокировки спутники находятся на синхронной орбите, такие как орбита Мимаса, их большая ось направлена ​​радиально к их планете.

Вращающееся тело из однородной самогравитирующей жидкости примет форму сфероида Маклорена (сплюснутый сфероид) или эллипсоида Якоби (разносторонний эллипсоид), когда оно находится в гидростатическом равновесии и при умеренных скоростях вращения. При более быстром вращении можно ожидать неэллипсоидальной грушевидной или яйцевидной формы, но они не стабильны.

Гидродинамика [ править ]

По вероятности и статистике [ править ]

f ( x ) = k ⋅ g ( ( x − μ ) Σ − 1 ( x − μ ) T ) <\displaystyle f(x)=k\cdot g\left((x-\mu )\Sigma ^<-1>(x-\mu )^<\mathsf>\right)>

Таким образом, функция плотности является скалярным преобразованием квадратичного выражения. Более того, уравнение для любой поверхности изоплотности утверждает, что выражение квадрики равно некоторой константе, специфичной для этого значения плотности, а поверхность изоплотности является эллипсоидом.

В высших измерениях [ править ]

x 1 2 a 1 2 + ⋯ + x n 2 a n 2 = 1. <\displaystyle <\frac ^<2>>^<2>>>+\cdots +<\frac ^<2>>^<2>>>=1.>

Источник