Чем объясняется различие температурных зависимостей сопротивления металла и полупроводника

Зависимость сопротивления металлов и полупроводников от температуры

При изменении температуры изменяется проводимость чистых металлов, сплавов и полупроводников.

Экспериментально установлено, что при повышении температуры сопротивление металлов увеличивается. При не слишком низких температурах сопротивление металлов растет пропорционально абсолютной температуре Т:

, (1)

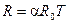
Соотношение (1) можно представить в виде

, (2)

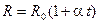
где – температура в o С, т.е. температурная зависимость сопротивления металлов линейна (рис.2).

Причинами электрического сопротивления в металлах являются посторонние примеси и физические дефекты кристаллической решетки металла, а также тепловое движение атомов металла, амплитуда колебаний которых зависит от температуры. Подвижность свободных носителей заряда (электронов) уменьшается при повышении температуры из-за возрастания числа столкновений с атомами кристаллической решетки металла, что приводит к росту сопротивления.

У полупроводников с ростом температуры подвижности носителей заряда (электронов и дырок) тоже падают, но это не играет заметной роли, т.к. рост концентрации является преобладающим. В результате сопротивление полупроводников с увеличением температуры Т практически уменьшается по экспоненциальному закону (рис.2):

, (3)

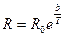
На рис.2 приведена зависимость электрического сопротивления полупроводников от температуры, эта зависимость носит резко выраженный характер.

Источник

Введение. Зависимость сопротивления полупроводников от температуры существенно отличается от подобной зависимости для металлов

Зависимость сопротивления полупроводников от температуры существенно отличается от подобной зависимости для металлов. В первую очередь отличие проявляется в том, что сопротивление полупроводников уменьшается с увеличением температуры, тогда как сопротивление металлов увеличивается.

Такое различие в характере проводимости металлов и полупроводников связано с различием структуры металлических и полупроводниковых кристаллов.

Объяснение свойств проводимости, достаточно хорошо согласующееся с экспериментом было получено на основе квантово-механической теории электропроводности кристаллов.

Взаимодействие атомов (молекул или ионов) в кристаллической решетке приводит к расщеплению энергетических уровней и образованию энергетических зон. Разрешенная зона (с уровнями разрешенных значений энергии), возникшая из уровня, на котором находятся валентные электроны (т.е. высший занятый энергетический уровень атома) образует валентную зону кристалла. Область, следующая за валентной, в которой отсутствуют разрешённые уровни энергии, называется запрещенной зоной. Следующая за валентной зоной зона разрешенных значений энергии называется свободной зоной.

Исходя из зонной теории, удается объяснить электрические свойства кристаллов.

Увеличение сопротивления металлов с температурой, в основном, обусловлено тем, что с увеличением температуры уменьшается время релаксации дрейфовой скорости электронов (сопротивление металлов обратно пропорционально времени релаксации) занимающих состояние вблизи уровня Ферми (Е_F) (именно эти электроны участвуют в проводимости).

Уровнем Ферми называется энергетический уровень, вероятность заполнения которого равна ½. При абсолютном нуле уровень Ферми совпадает с верхним заполненным электронами уровнем Е_F(0). В общем случае уровень Ферми зависит от температуры, однако эта зависимость достаточно слабая и во многих случаях для металлов можно полагать Е_F = Е_F(0).

Электропроводность полупроводников существенно зависит от наличия в полупроводнике определённых примесей. В случае чистых полупроводников говорят о собственной проводимости полупроводников.

Зонная диаграмма чистых полупроводников показана на рис. 1. Энергия Ферми для этого случая находится вблизи середины запрещённой зоны. Валентная зона полупроводников полностью заполнена и электроны не могут свободно перемещаться внутри полупроводника. Однако для полупроводников характерно малая ширина запрещенной зоны (много меньше, чем для диэлектриков), порядка нескольких десятых электронвольта и энергия теплового движения оказывается достаточной для того, чтобы перевести часть электронов в верхнюю свободную зону (для этого случая эта зона является зоной проводимости). Эти электроны могут изменять свою энергию под действием внешнего электрического поля и, следовательно, участвуют в проводимости. Кроме того, вследствие образования вакантных уровней в валентной зоне электроны этой зоны также могут изменять свою скорость под действием электрического поля и, следовательно, участвовать в проводимости. Поведение электронов валентной зоны может быть представлено как движение положительно заряженных квазичастиц, получивших название «дырок».

Рис. 1. Зонная диаграмма чистых полупроводников

Уменьшение сопротивления чистых полупроводников с температуройобъясняется тем, что с повышением температуры увеличивается число электронов перешедших в зону проводимости, а следовательно, и количество образовавшихся дырок, что приводит к увеличению носителей тока. Поскольку проводимость пропорциональна числу носителей, она также увеличивается с повышением температуры, а сопротивление уменьшается.

Зависимость удельной электропроводности от температуры определяется вероятностью заполнения электронов зоны проводимости, зависимость которой от температуры определяется выражением:

,

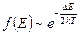
где DE – ширина запрещённой зоны; k – постоянная Больцмана; T – абсолютная температура.

Следовательно, удельная электропроводность с температурой изменяется по закону:

,

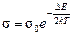
где s₀– величина, изменяющаяся с температурой гораздо медленнее, чем экспонента, в связи с чем её можно в первом приближении считать константой. Отсюда зависимость сопротивления от температуры определяется выражением:

, (1)

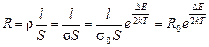
где R₀ – константа, практически независящая от температуры.

Собственная проводимость полупроводников при нормальных условиях достаточно мала.

Электропроводность чистых полупроводников при нормальных условиях достаточно мала, что ограничивает их практическое применение. Более широкое применение получили полупроводники с примесной проводимостью.

Примесная проводимость возникает при внедрении в кристаллическую решётку полупроводника атомов, валентность которых отличается от валентности основных атомов (как правило, на единицу). Существует два типа примесной проводимости: донорная (полупроводник n-типа) и акцепторная (полупроводник p-типа).

Донорная проводимость возникает при наличии атомов примеси, валентность которых больше валентности основных атомов. Для примера рассмотрим решетку германия (четырёхвалентный элемент) с примесью пятивалентных атомов фосфора. Такая схема условно изображена на рис. 2. Четыре электрона атома фосфора образуют ковалентные связи с соседними атомами германия. Следовательно, пятый валентный электрон оказывается как бы лишним и легко отщепляется от атома за счёт энергии теплового движения.

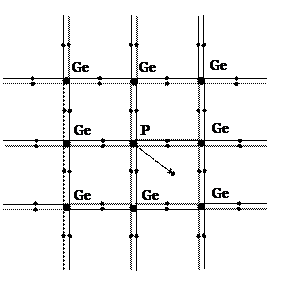
Рис. 2. Схема образования донорной проводимости в полупроводнике

Причём такое образование свободного электрона не приводит к образованию дырки, так как образованный при этом избыточный положительный заряд связан с атомом примеси и перемещаться по решётке не может.

По зонной теории примесь обладает собственным набором значений разрешённых энергий, что для определённых примесей приводит к возникновению на энергетической схеме примесных уровней, расположенных в запрещённой энергетической зоне кристалла. Донорная проводимость возникает, если примесные уровни, обусловленные примесью с валентностью большей, чем у основных атомов, расположены вблизи дна зоны проводимости (рис. 3), причём расстояние до дна много меньше ширины запрещённой зоны. Энергия Ферми для таких полупроводников приблизительно находится посередине между донорными уровнями и дном зоны проводимости.

Рис. 3. Энергетическая структура донорных полупроводников

Для таких полупроводников характерно, что концентрация электронов во много раз превышает концентрацию дырок.

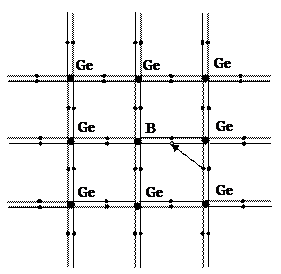
Акцепторнаяпроводимость возникает при наличии атомов примеси, валентность которых меньше валентности основных атомов. Для примера рассмотрим решетку германия (четырёхвалентный элемент) с примесью трёхвалентных атомов бора. Такая схема условно изображена на рис. 4. Три электрона атома бора образуют ковалентные связи с соседними атомами германия. Одна связь оказывается как бы незадействованной, что соответствует образованию свободного носителя дырки.

Рис. 4. Схема образования акцепторной проводимости в полупроводнике

Причём такое образование свободной дырки не приводит к образованию электрона, так как образованный при этом избыточный отрицательный заряд связан с атомом примеси и перемещаться по решётке не может.

По зонной теории акцепторная проводимость возникает, если примесные уровни, обусловленные примесью с валентностью меньшей, чем у основных атомов, расположены вблизи потолка валентной зоны (рис. 5), причём расстояние до валентной зоны много меньше ширины запрещённой зоны. Энергия Ферми для таких полупроводников приблизительно находится посередине между акцепторными уровнями и потолком валентной зоны.

Рис. 5. Энергетическая структура акцепторных полупроводников

Для таких полупроводников характерно, что концентрация дырок во много раз превышает концентрацию электронов.

В примесных полупроводниках кроме носителей, образованных за счёт примеси (основные носители), имеются и носители, образованные за счет собственной проводимости (неосновные носители).

Зависимость сопротивления примесных полупроводников от температуры существенно определяется диапазоном температур, в котором эта зависимость рассматривается. При достаточно малых температурах (для большинства примесных полупроводников до комнатной температуры) проводимость в основном определяется носителями, возникающих за счёт примеси. При малых температурах зависимость сопротивления от температуры подобна зависимости для чистых полупроводников, однако вместо ширины запрещённой зоны эта зависимость определяется энергией активации примесей E_a:

. (2)

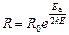
Причём энергия активации примеси много меньше ширины запрещённой зоны. При повышении температуры достаточно быстро достигается насыщение носителей, т.е. практически все носители перешли с примесных уровней (для донорных полупроводников) или на примесные уровни (для акцепторных полупроводников). В этом случае, количество носителей обусловленных примесью с увеличением температуры не изменяется и, сопротивление, как и для металлов, определяется временем релаксации дрейфовой скорости носителей. Следовательно, как и для металлов, сопротивление примесных полупроводников при этих температурах увеличивается. При больших температурах существенно проявляется собственная проводимость полупроводников, много превышающая проводимость, обусловленную примесями. В этом диапазоне сопротивление уменьшается по закону соответствующему выражению (1). В промежуточном диапазоне температур проявляется и примесная и собственная проводимость, что приводит к сложному характеру зависимости сопротивления от температуры.

Источник

Температурная зависимость электропроводимости металлов

ЛЕКЦИЯ 15. ТЕРМОПЕЗИСТОРЫ

1. Температурная зависимость электропроводимости металлов

Электропроводность металлов, полупроводников и диэлектриков связана с наличием в них свободных носителей зарядов: электронов и дырок и их упорядоченным движением под действием электрического поля E. Движение носителей заряда под действием магнитного поля в настоящей работе не рассматривается. Проводимость σ определяется формулой

где q – элементарный заряд, n – концентрация электронов, р – концентрация дырок, μn – подвижность электронов, μp – подвижность дырок.

Существует три типа металлов, отличающихся по типу проводимости: электронные (проводимость связана с движением электронов), дырочные (проводимость связана с движением дырок) и металлы со смешенным типом проводимости (проводимость связана с движением электронов и дырок). У всех типов металлов концентрация носителей заряда очень слабо зависит от температуры [1]. Например, у электронных металлов она равна концентрации валентных электронов и составляет n

1022 штук на кубический сантиметр.

Подвижность носителей определяется химическим составом, структурой кристаллической решетки и температурой металла. У чистых металлов с идеальной кристаллической решеткой при температуре Т=0 К электроны движутся по волновым коридорам вдоль атомов, расположенных в узлах кристаллической решетки, при этом средняя длина свободного пробега электронов велика и сопротивление минимально. У некоторых металлов наблюдается явление сверхпроводимости. В настоящем издании это явление не рассматривается.

В реальных кристаллах всегда имеются атомы примесей и дефекты кристаллической решетки. На этих неоднородностях происходит рассеяние электронов, что приводит к уменьшению средней длины свободного пробега и увеличению электрического сопротивления. Это явление определяет сопротивление проводников при низких температурах. При Т>0 К атомы совершают тепловые колебания и возникает рассеяние электронов на тепловых колебаниях решетки. При повышении температуры это явление в основном обуславливает величину электрического сопротивления. Подвижность носителей заряда определяется средней длиной свободного пробега электронов.

Для практических целей определения удельного сопротивления чистого металла ρ часто используют формулу

где ρ0 – удельное сопротивление при комнатной температуре, a – положительный, слабо зависящий от температуры температурный коэффициент сопротивления металлов.

2. Температурная зависимость электропроводимости полупроводников и диэлектриков

, (3)

где k = 0.86·10−4 эВ/К постоянная Больцмана, mn* и mp* ‑ эффективные массы электронов и дырок. Если mn* ≈ mp* и полупроводник широкозонный ΔW = Wc − Wv

1 эВ, то второй член при Т = 300 К имеет порядок 0.03 эВ и слабо изменяет положение уровня энергии Ферми. Вплоть до температур плавления вкладом второго члена можно пренебречь и считать WFi не зависящей от температуры (горизонтальная пунктирная линия на рис.1,а).

При Т = 0 К все электроны “связаны со своими атомами” и свободных носителей заряда нет. Полупроводник является идеальным изолятором. При повышении температуры начинаются тепловые колебания атомов кристаллической решетки. В результате электрон может получить энергию, достаточную для преодоления запрещенной зоны, и попасть в зону проводимости. Такой процесс называется тепловой генерацией пары электрон – дырка. Электрон совершает хаотические (броуновские) движения по всему объему полупроводника в межатом-ном пространстве. Дырки также хаотически перемещаются, но только по межатомным электронным связям. Через некоторое время τ электрон рекомбинирует с дыркой, но в другом месте полупроводника появится новая пара. Равновесные концентрации электронов и дырок ni, дырок pi равны и определяются:

где Nc =2(2πmn*kT/h2)3/2 – плотность квантовых состояний у дна зоны проводимости, Nv = 2(2πmp*kT/h2)3/2 – плотность квантовых состояний у верха валентной зоны, а h = 4.14·10−15 эВ·c ‑ постоянная Планка.

Экспоненциальная зависимость концентрации свободных носителей от температуры показана на рис.1,а жирной линией. В собственном полупроводнике концентрация свободных носителей заряда при всех температурах, вплоть до температуры плавления, существенно меньше концентрации валентных электронов, поэтому проводимость полупроводников на несколько порядков меньше проводимости металлов. Исключение составляют вырожденные полупроводники, у которых уровень Ферми располагается в зоне проводимости. Это может произойти при нагревании узкозонных полупроводников, у которых ΔW

В примесном полупроводнике n-типа уровень энергии Wd валентного электрона атома донорной примеси, который не участвует в образовании ковалентных связей с соседними атомами полупроводника, располагается в запрещенной зоне недалеко от дна зоны проводимости (рис.1,б). В этом случае при Т = 0 К уровни энергии валентной зоны и примеси заполнены электронами, в зоне проводимости электронов нет и уровень Ферми располагается посередине между Wd и Wс. Энергетический зазор ΔWn = Wc − Wd Ti концентрация тепловых электронов и дырок становится больше концентрации примесных электронов и вклад собственной проводимости становится определяющим. При этом уровень Ферми асимптотически стремится к положению уровня Ферми в собственном полупроводнике WFi.

На длину свободного пробега и подвижность носителей заряда в основном влияют два физических фактора: рассеяние носителей заряда на тепловых колебаниях атомов кристаллической решетки и рассеяние на ионах примесей. При больших температурах преобладает рассеяние на тепловых колебаниях атомов, и с ростом температуры подвижность уменьшается. В диапазоне низких температур уменьшаются тепловые скорости движения электронов и увеличивается время воздействия электрического поля иона примеси на носители заряда, поэтому подвижность падает. Зависимость μ = f(T) для разных концентраций примесей N приведена на рис.2. При увеличении концентрации примесей в области низких температур μ уменьшается. В области высоких температур преобладает рассеяние на тепловых колебаниях атомов кристаллической решетки, и подвижность слабо зависит от концентрации примесей.

При большой напряженности электрического поля Е в полупроводнике происходит “разогрев” электронов: их дрейфовая скорость становится соизмеримой со скоростью хаотического теплового движения, что приводит к увеличению числа столкновений. При этом средняя длина свободного пробега уменьшается, а подвижность начиная с Екр

104 В/см падает (рис.3).

Для собственных полупроводников во всем интервале температур основной вклад в изменение проводимости вносит изменение концентрации носителей заряда:

где σ0 = q(μnNc +μрNv) – коэффициент, слабо зависящий от температуры.

Для примесных полупроводников сильная температурная зависимость проводимости наблюдается в области температур ионизации примесей Ts. При этом вклад тепловых электронов и дырок можно не учитывать и проводимость

где σ0n = qμnNc и σ0р = qμрNv – коэффициенты, слабо зависящие от температуры.

В области температур выше Ts и ниже Ti проводимость примесных полупроводников слабо зависит от температуры. В этой температурной области работают полупроводниковые диоды, транзисторы и интегральные микросхемы. При Т > Ti примесные полупроводники обычно не используют.

3. Параметры и характеристики терморезисторов

Терморезисторы могут изготавливаться из собственных полупроводников с малой шириной запрещенной зоны ΔW или из примесных полупроводников с высокой температурой активации примеси Ts.

Основной характеристикой терморезистора является температурная зависимость его сопротивления R. Она совпадает с температурной зависимостью удельного сопротивления полупроводника ρ, из которого изготовлен терморезистор. Во всем диапазоне рабочих температур эта зависимость достаточно точно определяется соотношением

где R¥ — коэффициент, зависящий от исходного материала и конструкции терморезистора, B – коэффициент температурной чувствительности, характеризующий физические свойства материала терморезистора. Его можно найти экспериментально

К, (10)

измерив Rком – сопротивление терморезистора при комнатной температуре Тком и R1 – сопротивление при повышенной температуре Т1.

Рассчитав коэффициент температурной чувствительности, можно найти ширину запрещенной зоны собственного полупроводника из формул (9) и (7) с учетом, что R

где Bn, и Bр, ‑ коэффициенты температурной чувствительности полупроводников n— и р-типа.

Температурный коэффициент сопротивления терморезистора

К−1. (13)

ТКRТ зависит от температуры, поэтому необходимо указывать температуру, при которой он получен (подстрочный индекс Т).

Зависимость ТКR=f(T) можно получить из (13) и (9):

Статическая вольт-амперная характеристика (ВАХ) терморезистора – это зависимость напряжения на терморезисторе от силы тока в условиях теплового равновесия между терморезистором и окружающей средой. На рис.4 показаны ВАХ терморезисторов с различными коэффициентами температурной чувствительности. Линейность ВАХ при малых токах и напряжениях связана с тем, что выделяемая в терморезисторе мощность недостаточна для существенного изменения его температуры. При увеличении тока, проходящего через терморезистор, выделяемая в нем мощность приводит к повышению температуры, росту концентрации свободных носителей заряда и уменьшению сопротивления. Линейность ВАХ нарушается. При дальнейшем увеличении тока и большой температурной чувствительности терморезистора может наблюдаться падающий участок ВАХ (участок с отрицательным дифференциальным сопротивлением).

Для каждой точки статической ВАХ терморезистора выполняется уравнение теплового баланса между мощностью электрического тока, выделяющейся в терморезисторе, и мощностью, которую он рассеивает в окружающую среду:

где Н [Вт/К]– коэффициент рассеяния терморезистора, численно равный мощности, которую нужно выделить в терморезисторе, чтобы его температура увеличилась на 1 К, Т – температура терморезистора, Tокр – температура окружающей среды.

Максимально допустимая температура терморезистора – это температура, при которой еще не происходит необратимых изменений параметров и характеристик терморезистора.

Максимально допустимая мощность рассеяния терморезистора Рmax – это мощность, при которой терморезистор, находящийся в спокойном воздухе при температуре 20ºС, разогревается при прохождении тока до максимально допустимой температуры.

Основное количество терморезисторов, выпускаемых промышленностью, изготовлено из оксидных полупроводников, а именно из оксидов металлов переходной группы Периодической системы элементов (от титана до цинка). Электропроводность оксидных полупроводников с преобладающей ионной связью отличается от электропроводности классических ковалентных полупроводников. Для металлов переходной группы характерны незаполненные электронные оболочки и переменная валентность. В результате электропроводность таких оксидов связана с обменом электронами между соседними ионами (“прыжковый” механизм). Энергия, необходимая для стимулирования такого обмена, экспоненциально уменьшается с увеличением температуры. Температурная зависимость сопротивления оксидного терморезистора аппроксимируется уравнением (9) для классических ковалентных полупроводников. Коэффициент температурной чувствительности В (10) отражает интенсивность обмена между соседними ионами, а ΔW – энергию обменной связи (11).

Источник