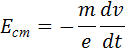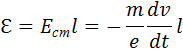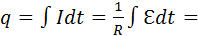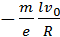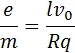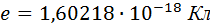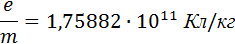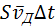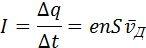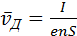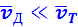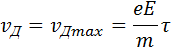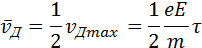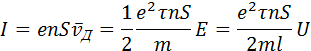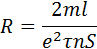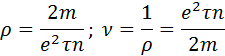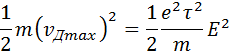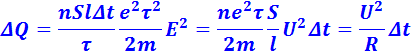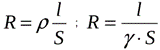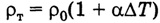Электронная теория проводимости

Электропроводность твердых тел обусловлена коллективным направленным движением свободных электронов.

К концу XIX века ученые знали связь между электрическим сопротивлением, силой тока и напряжением, которая описывается законом Ома. Благодаря эффекту Холла знали они и то, что носителями электрического тока в металлах являются отрицательно заряженные электроны. Оставалось составить описание электрического сопротивления на атомном уровне. Первую попытку такого рода предпринял в 1900 году немецкий физик Пауль Друде (Paul Drude, 1863–1906).

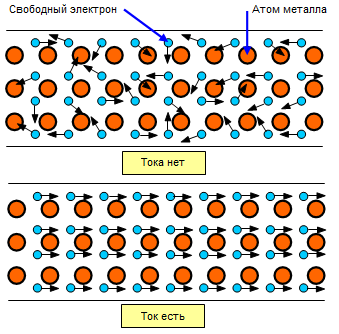
Смысл электронной теории проводимости сводится к тому, что каждый атом металла отдает валентный электрон из внешней оболочки, и эти свободные электроны растекаются по металлу, образуя некое подобие отрицательно заряженного газа. Атомы металла при этом объединены в трехмерную кристаллическую решетку, которая практически не препятствует перемещению свободных электронов внутри нее (см. Химические связи). Как только к проводнику прикладывается электрическая разность потенциалов (например, посредством замыкания на два его конца двух полюсов аккумуляторной батареи), свободные электроны приходят в упорядоченное движение. Сначала они движутся равноускоренно, но длится это недолго, поскольку очень скоро электроны перестают ускоряться, сталкиваясь с атомами решетки, которые, в свою очередь, от этого начинают колебаться всё с большей амплитудой относительно условной точки покоя, и мы наблюдаем термоэлектрический эффект разогревания проводника.

На электроны же эти столкновения оказывают затормаживающее воздействие, аналогично тому, как, допустим, человеку тяжело с достаточно большой скоростью передвигаться в плотной людской толпе. В результате скорость электронов устанавливается на некоей усредненной отметке, которая называется скоростью миграции, и скорость эта, на самом деле, отнюдь не высока. Например, в обычной бытовой электропроводке средняя скорость миграции электронов составляет всего несколько миллиметров в секунду, то есть, электроны отнюдь не летят по проводам, а скорее ползут по ним темпами, достойными разве что улитки. Свет же в лампочке зажигается практически моментально лишь потому, что с места все эти медлительные электроны трогаются одновременно, как только вы нажимаете на кнопку выключателя, и электроны в спирали лампочки также приходят в движение сразу же. То есть, нажимая на кнопку выключателя, вы производите в проводах эффект, аналогичный тому, как если бы включили насос, подсоединенный к поливочному шлангу, до отказа заполненному водой, — струя на противоположном от насоса конце хлынет из шланга незамедлительно.

Друде весьма серьезно подошел к описанию свободных электронов. Он предположил, что внутри металла они ведут себя подобно идеальному газу, и применил к ним уравнение состояния идеального газа, достаточно справедливо проведя аналогию между соударениями электронов и тепловыми соударениями молекул идеального газа. Это позволило ему сформулировать формулу электрического сопротивления, как функции среднего времени между соударениями свободных электронов с атомами кристаллической решетки. Подобно многим простым теориям, электронная теория проводимости хорошо описывает некоторые основные явления из области электропроводности, но бессильна описать многие нюансы этого явления. В частности, она не только не объясняет явления сверхпроводимости при сверхнизких температурах (см. Теория сверхпроводимости, но, напротив, предсказывает неограниченный рост электрического сопротивления любого вещества при стремлении его температуры к абсолютному нулю. Поэтому сегодня электропроводящие свойства вещества принято интерпретировать в рамках квантовой механики (см. Уравнение Шрёдингера).

Источник

Электрический ток в металлах

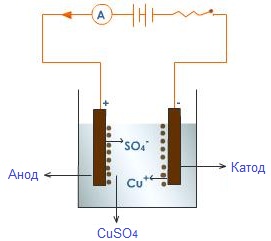
Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л.И. Мандельштаму и Н.Д. Папалекси В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.

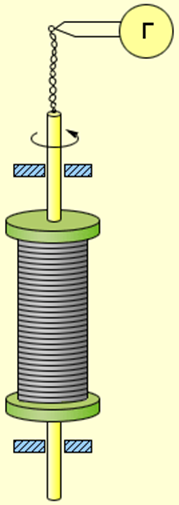
Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

Схема опыта Толмена и Стюарта

При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила 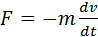которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью E_ст поля сторонних сил:

Следовательно, в цепи при торможении катушки возникает электродвижущая сила 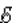, равная

где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный

Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ₀ – начальная линейная скорость проволоки.

Отсюда удельный заряд e / m свободных носителей тока в металлах равен:

Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.

По современным данным модуль заряда электрона (элементарный заряд) равен

а его удельный заряд есть

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.

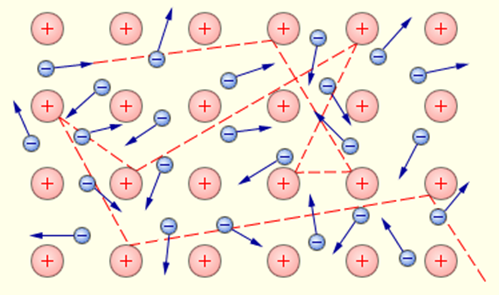
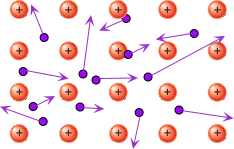
Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).

Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером.

Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость 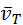теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость 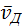дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме

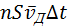
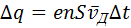
Число таких электронов равно , где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Отсюда следует:

или

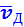
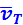
средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения

Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.

Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа 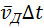сильно преувеличены

Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.

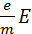
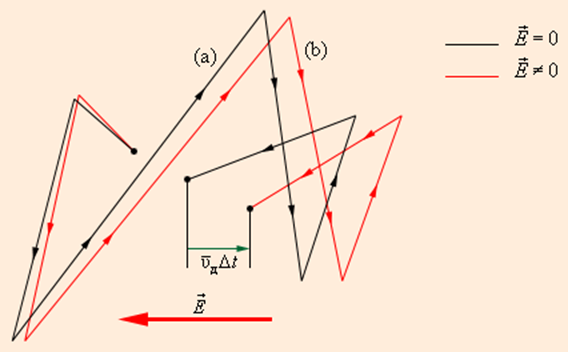
Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение . Поэтому к концу свободного пробега дрейфовая скорость электрона равна

где τ – время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа 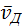равно половине максимального значения:

Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде:

где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно:

а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями:

Закон Джоуля-Ленца.

К концу свободного пробега электроны под действием поля приобретают кинетическую энергию

Согласно сделанным предположениям вся эта энергия при соударениях передается решетке и переходит в тепло.

За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:

Это соотношение выражает закон Джоуля-Ленца.

Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.

Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти, см. ч. I, § 3.10). Наличие свободных электронов на сказывается на величине теплоемкости металлов.

Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает соотношение 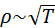, в то время как из эксперимента получается зависимость ρ

T. Однако наиболее ярким примером расхождения теории и опытов является сверхпроводимость.

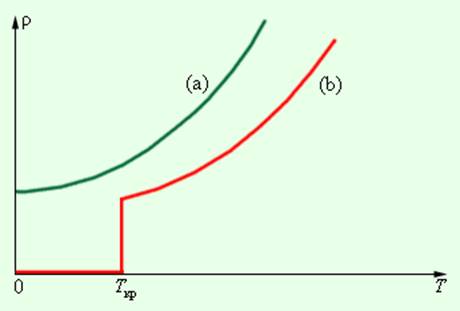
Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах. При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое датским физиком Х.Каммерлинг-Онесом в 1911 году. При некоторой определенной температуре T_кр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni₃Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.

Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник

Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи.

Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.

Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении был сделан в 1986 году, когда было обнаружено, что у одного сложного керамического соединения T_кр = 35 K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью. В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125 К.

В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями T_кр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей.

Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.

Источник

Электропроводность веществ

В этой статье раскроем тему электропроводности, вспомним о том, что такое электрический ток, как он связан с сопротивлением проводника и соответственно с его электропроводностью. Отметим основные формулы для вычисления данных величин, коснемся темы скорости тока и ее связи с напряженностью электрического поля. Также затронем связь электрического сопротивления и температуры.

Для начала вспомним о том, что же такое электрический ток. Если поместить вещество во внешнее электрическое поле, то под действием сил со стороны этого поля, в веществе начнется движение элементарных носителей заряда — ионов или электронов. Это и будет электрическим током. Сила тока I измеряется в амперах, и один ампер — это ток, при котором через поперечное сечение проводника протекает за секунду заряд, равный одному кулону.

Ток бывает постоянным, переменным, пульсирующим. Постоянный ток не меняет своей величины и направления в каждый конкретный момент времени, переменный ток с течением времени меняет свои величину и направление (генераторы переменного тока и трансформаторы дают именно переменный ток), пульсирующий ток меняет свою величину, но не меняет направления (например выпрямленный переменный ток является пульсирующим).

Вещества имеют свойство проводить электрический ток под действием электрического поля, и это свойство называется электропроводностью, которая у разных веществ различна. Электропроводность веществ зависит от концентрации в них свободных заряженных частиц, то есть ионов и электронов, не связанных ни с кристаллической структурой, ни с молекулами, ни с атомами данного вещества. Так, в зависимости от концентрации в веществе свободных носителей заряда, вещества по степени электропроводности подразделяются на: проводники, диэлектрики и полупроводники.

Наиболее высокой электропроводностью обладают проводники электрического тока, и по физической природе, проводники в природе представлены двумя родами: металлами и электролитами. В металлах ток обусловлен перемещением свободных электронов, то есть проводимость у них электронная, а в электролитах (в растворах кислот, солей, щелочей) — перемещением ионов — частей молекул, имеющих положительный и отрицательный заряд, то есть проводимость у электролитов ионная. Ионизированные пары и газы отличаются смешанной проводимостью, в них ток обусловлен движением и электронов и ионов.

Электронная теория отлично объясняет высокую электропроводность металлов. Связь валентных электронов с их ядрами в металлах слаба, потому эти электроны свободно перемещаются от атома к атому по объему проводника.

Получается, что свободные электроны в металлах заполняют пространство между атомами подобно газу, электронному газу, и находятся в хаотичном движении. Но при внесении металлического проводника в электрическое поле, свободные электроны станут двигаться упорядоченно, они переместятся по направлению к положительному полюсу, чем создадут ток. Таким образом, упорядоченное движение свободных электронов в металлическом проводнике называется электрическим током.

Известно, что скорость распространения электрического поля в пространстве примерно равна 300000000 м/с, то есть скорости света. Это та же скорость, с которой ток проходит по проводнику.

Что это значит? Это не значит, что каждый электрон в металле движется с такой огромной скоростью, электроны в проводнике напротив — имеют скорость от нескольких миллиметров в секунду до нескольких сантиметров в секунду, в зависимости от напряженности электрического поля, а вот скорость распространения электрического тока по проводнику как раз равна скорости света.

Все дело в том, что каждый свободный электрон оказывается в общем электронном потоке того самого «электронного газа», и во время прохождения тока, электрическое поле оказывает действие на весь этот поток, в итоге электроны непрерывно друг другу передают это действие поля — от соседа к соседу.

Но движутся электроны на своих местах очень медленно, несмотря на то, что скорость распространения электрической энергии по проводнику оказывается огромной. Так, когда на электростанции включают рубильник, ток мгновенно возникает во всей сети, а электроны при этом практически стоят на местах.

Однако, когда свободные электроны движутся по проводнику, они испытывают многочисленные столкновения на своем пути, они сталкиваются с атомами, ионами, молекулами, передавая им часть своей энергии. Энергия движущихся электронов, преодолевающих такое сопротивление, частично рассеивается в виде тепла, и проводник нагревается.

Эти столкновения служат сопротивлением движению электронов, потому свойство проводника препятствовать движению заряженных частиц и называют электрическим сопротивлением. При малом сопротивлении проводника проводник нагревается током слабо, при значительном — намного сильнее, и даже до бела, этот эффект применяется в нагревательных приборах и в лампах накаливания.

Единица изменения сопротивления — Ом. Сопротивление R = 1 Ом — это сопротивление такого проводника, при прохождении по которому постоянного тока в 1 ампер, разность потенциалов на концах проводника равна 1 вольту. Эталон сопротивления в 1 Ом — столб ртути высотой 1063 мм, сечением 1 кв.мм при температуре 0°С.

Поскольку проводникам характерно электрическое сопротивление, то можно сказать, что в какой-то степени проводник способен проводить электрический ток. В связи с этим введена величина, называемая проводимостью или электропроводностью. Электропроводность — это способность проводника проводить электрический ток, то есть величина, обратная электрическому сопротивлению.

Единица измерения электропроводности G (проводимости) — Сименс (См), и 1 См = 1/(1 Ом). G = 1/R.

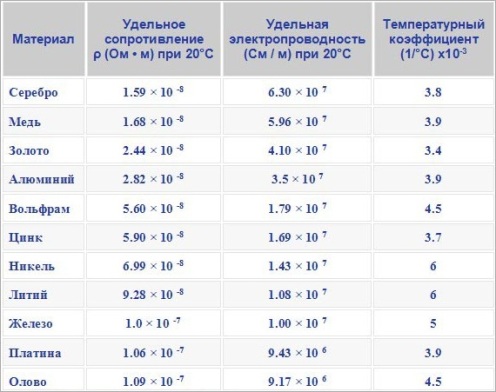
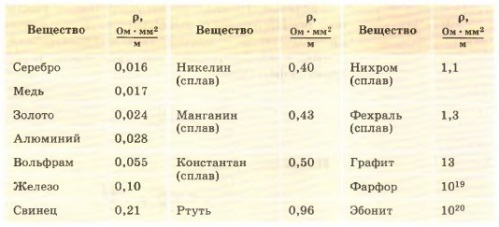
Так как атомы различных веществ в разной степени препятствуют прохождению электрического тока, то и электрическое сопротивление у различных веществ разное. По этой причине введено понятие удельное электрическое сопротивление, величина которого «р» характеризует проводящие свойства того или иного вещества.

Сегодня проводящие материалы в электротехнике используют в основном в виде лент, шин, проволок, с определенной площадью поперечного сечения и определенной длины, но не в виде метровых кубов. И для более удобных расчетов электрического сопротивления и электропроводности проводников конкретных размеров были введены более приемлемые единицы измерения как для удельного электрического сопротивления, так и для удельной электропроводности. Ом*мм2/м — для удельного сопротивления, и См*м/мм2 — для удельной электропроводности.

Теперь можно говорить, что удельное электрическое сопротивление и удельная электропроводность характеризуют проводящие свойства проводника площадью поперечного сечения в 1 кв.мм, длиной в 1 метр при температуре 20°C, это более удобно.

Лучшей электропроводностью обладают такие металлы как: золото, медь, серебро, хром, алюминий. Сталь и железо проводят ток хуже. Чистые металлы всегда обладают лучшей электропроводностью, чем их сплавы, поэтому чистая медь в электротехнике предпочтительней. Если нужно специально высокое сопротивление, то используют вольфрам, нихром, константан.

Зная величину удельного электрического сопротивления или удельной электропроводности, можно легко вычислить сопротивление или электропроводность конкретного проводника, изготовленного из данного материала, приняв в расчет длину l и площадь поперечного сечения S этого проводника.

При понижении температуры — наоборот, колебания атомов кристаллической решетки становятся меньше, сопротивление уменьшается (возрастает электропроводность). У одних веществ зависимость сопротивления от температуры выражена слабее, у других — сильнее. Например такие сплавы как константан, фехраль и манганин слабо меняют удельное сопротивление в определенном интервале температур, поэтому из них делают термостабильные резисторы.

Зная температурный коэффициент сопротивления и приращение температуры, можно легко вычислить удельное сопротивление вещества при заданной температуре.

Источник