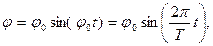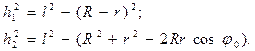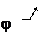Чем обусловлено возникновение возвращающего момента при повороте трифилярного подвеса

МЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА

Цель работы: определение момента инерции некоторых тел относительно оси вращения, проходящей через центр масс, иссле­дование влияния на момент инерции переноса осей вращения (про­верка теоремы Штейнера методом крутильных колебаний).

Принадлежности: трифилярный подвес, секундомер, штан­ген­циркуль, тела для измерения момента инерции.

Вопросы, знание которых необходимо для допуска к выполнению работы

1. Угловая скорость. Связь между угловой скоростью тела и ли­нейной скоростью его точек. Единицы измерения.

2. Угловое ускорение. Связь между угловым ускорением тела и линейным ускорением его точек. Единицы измерения.

3. Что называется плечом силы?

4. Что называется моментом силы? Чем обусловлены его величина и направление? Единицы измерения.

5. Что называется моментом инерции твердого тела? Единицы из­мерения. От чего зависит величина момента инерции?

6. Напишите и поясните основное уравнение динамики вращательного движения. Какова роль момента инерции в этом уравнении?

7. Сформулируйте теорему Штейнера.

8. В чем отличие крутильных колебаний от колебаний физического маятника?

9. Почему натяжение нитей трифилярного подвеса должно быть одинаково?

10. Под действием какой силы трифилярный подвес совершает кру­тильные колебания?

11. Расскажите порядок выполнения работы.

. (1)

Величина момента инерции тела зависит от характера распределения масс относительно оси вращения и поэтому одно и то же тело может иметь разные моменты инерции относительно разных осей.

Если тело может вращаться вокруг неподвижной оси, то изменение его движения зависит от действующего на него момента силы. Моментом силы относительно неподвижной оси называется величина, численно равная произведению силы F на ее плечо h. Плечо силы – есть кратчайшее расстояние от центра вращения до линии действия силы.

Вращательное движение тела характеризуется угловой скоростью w и угловым ускорением b:

w = ; b = , (3)

Основной закон динамики вращательного движения, выражающий зависимость углового ускорения от момента силы, записывается в виде:

. (4)

Так как момент инерции зависит от расстояния массы относитель­но оси вращения, то при смеще­нии оси момент инерции изменяется. Момент инерции тела относительно оси, проходящей через центр масс (J₀), в большинстве случаев определить нетруд­но. В этом случае, зная момент инерции относительно оси вращения, проходящей через центр масс, можно найти момент относительно любой оси, параллельной первой.

Для случая параллельных осей применима теорема Штейнера: момент инерции относительно любой оси вращения равен сумме момента инерции относительно оси вращения, проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями (d):

.

На практике момент инерции тела мож­но определить методом трифилярного подвеса.

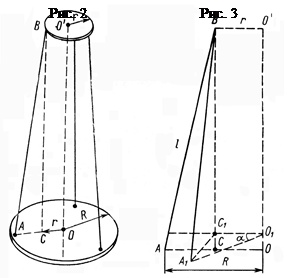
Трифилярный под­вес представляет собой круглую платформу, подвешенную на трех симметрично расположенных нитях, укреплен­ных у краев этой платформы. Наверху эти нити также симметрично прикреплены к диску несколько меньшего диаметра, чем диаметр платформы (рис. 2).

. (6)

Считая, что платформа совершает гармонические колебания, можем написать зависимость углового смещения j платформы от времени в виде:

, (7)

. (8)

В момент прохождения через положение равновесия (t = 0; (1/2)T; (3/2)Т и т.д.) абсолютное значение этой величины будет

. (9)

. (10)

.

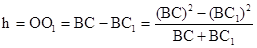
то .

Источник

Определение момента инерции твердых тел методом трифилярного подвеса

В природе и технике весьма распространенным является вращательное движение, которое описывается в физике основным законом вращательного движения. Этот закон в случае неподвижной оси вращения можно рассматривать как аналог II закона Ньютона, в котором роль меры инертности играет момент инерции абсолютно твердого тела. Расчет момента инерции твердого тела относительно произвольной оси является в общем случае сложной математической задачей. В данной лабораторной работе приводятся методы решения таких задач экспериментальным путем и расчетным относительно главных (свободных) осей вращения твердых тел. Расчеты приведены в Приложении к работе.

Цель работы. Экспериментальное определение момента инерции диска, цилиндра, кольца и параллелепипеда относительно главных (свободных) осей инерции этих твердых тел; исследование зависимости момента инерции от распределения массы тела относительно оси вращения.

Практическая ценность. В работе изучается используемый в практике метод измерения момента инерции твердых тел. В процессе работы студенты получают навыки измерения момента инерции твердых тел методом крутильных колебаний трифилярного подвеса и умение рассчитывать момент инерции относительно осей симметрии тела.

1. Теоретическая часть

Рассмотрим твердое тело, которое может вращаться около оси . Разобьем его на большое число (n) малых объемов с массами и будем рассматривать каждый такой элемент в виде материальной точки. Через обозначим соответствующее расстояние от материальной точки до оси (рис.1). Величина называется моментом инерции данной материальной точки относительно оси вращения . Момент инерции всего тела относительно будет равен сумме моментов инерции всех материальных точек, на которые мы разбили твердое тело:

.

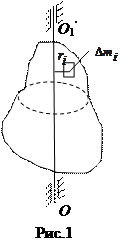
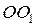
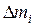
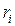
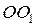
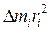
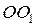
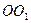
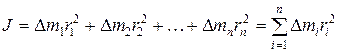
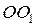
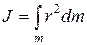
Следует заметить, что величина момента инерции твердого тела зависит не только от величины массы тела, но также от распределения массы тела относительно оси вращения. Если вещество в теле распределено непрерывно, то сумма заменяется интегралом и момент инерции тела относительно запишется:

, (1)

где 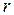— расстояние от элементарной массы dm до оси вращения.

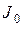
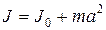
Если известен момент инерции тела относительно оси, проходящей через его центр масс , то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:

, (2)

где 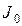— момент инерции тела относительно оси, проходящей через центр масс; m – масса тела, а – расстояние между осями.

2. Экспериментальная часть

2.1. Выбор методики эксперимента:

Если платформа массой m, вращаясь в одном направлении, поднялась на высоту h, то потенциальная энергия в крайнем верхнем положении

,

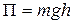
где g – ускорение свободного падения тела.

Вращаясь в другом направлении, платформа придет в положение равновесия с кинетической энергией, равной

,

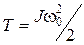
где J – момент инерции платформы, 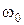— угловая скорость в момент достижения ею положения равновесия.

Пренебрегая работой сил трения, на основании закона сохранения механической энергии имеем

. (3)

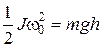
Считая, что платформа совершает гармонические колебания, можно написать зависимость угла поворота платформы от времени:

,

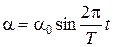
где α – мгновенное значение угла поворота платформы; — амплитудное значение угла поворота, Т – период полного колебания; t— время.

Угловая скорость ω является первой производной от угла поворота α по времени:

.

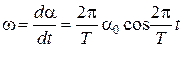
В момент прохождения через положение равновесия абсолютное значение угловой скорости будет максимальным:

. (4)

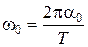
Подставляя это значение в уравнение (3), получим

. (5)

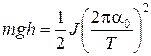
Учитывая, что при малых углах поворота

,

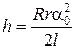
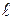
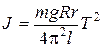
где R – расстояние от оси платформы до точек закрепления проволок на платформе; r – расстояние от оси платформы до точек закрепления проволоки на треноге; – длина каждой проволоки подвеса, окончательно получаем

. (6)

По этой формуле может быть определен момент инерции платформы и тела, положенного на нее, так как все величины в правой части могут быть непосредственно измерены. В случае нагруженной платформы массу m берут равной сумме масс платформы и тела. Вычисленный момент инерции системы складывается из момента инерции пустой платформы и тела:

, (7)

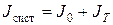
где 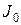— момент инерции платформы; — момент инерции тела.

Из соотношения (7) определяется момент инерции тела

. (8)

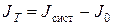
2.2. Работа на экспериментальной установке

Платформа в нерабочем положении арретирована, т.е. покоится на столике, который можно опускать и поднимать, закрепляя на нужной высоте с помощью специального винта на штативе. Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем поворота треноги вокруг ее оси с помощью шнура, приводящего в движение рычажок, связанный с треногой. Этим достигается почти полное отсутствие других, некрутильных колебаний, затрудняющих измерения.

2.3. Задание 1. Определение момента инерции ненагруженной платформы

1. Разарретировав платформу (опустив столик под платформой), плавным натяжением шнура сообщают ей вращательный импульс, в результате чего платформа придет в колебательное движение.

3. Усредняют результат измерения времени:

(9)

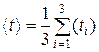
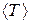
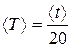
и находят период колебаний ненагруженной платформы по формуле

. (10)

4. По формуле (6) рассчитывают момент инерции пустой платформы .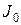

2.4. Задание 2. Определение моментов инерции конкретных тел опытным путем.

1. Нагружают платформу таким образом, чтобы конкретное тело (диск, цилиндр, кольцо или параллелепипед выбирается по указанию преподавателя) вписалось в соответствующие контуры, изображенные на платформе трифилярного подвеса.

2. Нагруженную платформу разарретируют и измеряют время 20 полных колебаний. Измерение повторяют 3 раза.

3. Аналогично из соотношений (9,10) определяют средний период колебаний нагруженной платформы.

4. Рассчитывают момент инерции нагруженной платформы по формуле (6).

5. По формуле (8) находят момент инерции конкретного тела .

2.5. Задание 3. Определение моментов инерции конкретных тел теоретическим путем.

1. Измеряют штангенциркулем все необходимые размеры предложенных тел (диска, цилиндра, кольца, параллелепипеда, пустой платформы).

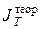
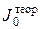
2. Моменты инерции конкретного тела и пустой платформы теоретически рассчитывают по формулам, указанным в Приложении.

3. Результаты расчетов для анализа сводят в следующую таблицу.

Конкретное тело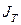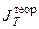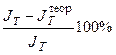
пустая платформа
диск
кольцо
параллелепипед

Измерения и расчет момента инерции параллелепипеда производится в трех плоскостях.

Последняя графа дает возможность оценить относительное расхождение теоретических и экспериментальных результатов. Проанализируйте и объясните полученные результаты.

1. Что называется моментом инерции абсолютно твердого тела относительно оси вращения? От чего он зависит? Теорема Штейнера (на примере решения задачи 3-2).

2. Как теоретически подсчитать момент инерции тела (параллелепипеда, цилиндра, стержня, шара, конуса) относительно главных осей?

3. Угловая скорость и угловое ускорение. Направление и модуль каждой из этих величин (на примере данной работы).

4. Основной закон динамики вращательного движения (в векторном виде) для твердого тела, ось вращения которого закреплена в подшипнике. Как он запишется для крутильных колебаний платформы?

5. Направление углового ускорения и угловой скорости при подъеме и спуске платформы?

6. В чем сущность закона сохранения механической энергии? При каких условиях справедлив закон сохранения механической энергии? В какой форме он записывается в данной работе?

7. Метод определения момента инерции тела, помещенного на платформу.

Источник

Определение момента инерции твердого тела методом трифилярного подвеса

На правах рукописи

Министерство образования Российской Федерации

Волгоградская государственная архитектурно-строительная академия

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ

МЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА

Волгоград 2010

Определение удельной теплоемкости металлов методом охлаждения: Методические указания к лабораторной работе №6 / Сост. ; ВолгГАСА. – Волгоград, 2002. – 8 с.

Целью работы является определение удельной и молярной теплоемкостей алюминия, проверка закона Дюлонга и Пти. Приводится краткая теория явления стационарной теплопроводности. Дано описание экспериментальной установки, а также порядок выполнения работы, способ расчета и графического представления результатов, сформулировано задание для учебно-исследовательской работы.

Для студентов всех специальностей.

Ил. 1. Табл. 1. Библиогр. 4 назв.

© Волгоградская государственная архитектурно-строительная академия, 2002

Цель работы — определение момента инерции твердого тела, проверка теоремы Штейнера.

Приборы и принадлежности: трифилярный подвес, электронный секундомер, тело для измерения момента инерции в виде разрезанного на две части диска.

1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Моментом инерции материальной точки называется произведение массы точки на квадрат расстояния до оси вращения J=mr2. Момент инерции системы материальных точек равен сумме моментов инерции всех точек системы относительно оси вращения

что, по определению, при Dm® 0 представляет собой интеграл

Интеграл легко вычисляется для однородных тел симметричной формы относительно оси, проходящей через центр инерции. Например, для диска радиусом R и массой m момент инерции относительно оси, проходящей через центр инерции перпендикулярно плоскости диска, равен J=mR2/2.

На практике момент инерции тела можно определить методом трифилярного подвеса, который представляет собой круглую платформу радиусом r1 и массой m, подвешенную к неподвижному диску радиусом r2 на трех симметрично расположенных нитях длиной l (см. рисунок).

Если повернуть платформу вокруг вертикальной оси ОО на угол j, то возникает момент сил, обусловленный суммарным действием силы тяжести и натяжения нити и стремящийся вернуть платформу в положение равновесия. Платформа начнет совершать крутильные колебания вокруг оси ОО. Полная механическая энергия платформы E складывается из кинетической энергии Jw2/2 и потенциальной mgh

где h – высота, на которую приподнимается центр тяжести платформы при повороте от положения равновесия,

— угловая скорость платформы.

Выражение для высоты, на которую приподнимается центр тяжести платформы, получим, анализируя рисунок.

Источник

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИМЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА

Лабораторная работа № 4.4

Цель работы: изучение законов динамики вращательного движения и экспериментальное определение момента инерции тел вращения с помощью трифилярного подвеса.

П ринадлежности: трифилярный подвес, секундомер, штангенциркуль, образцы для измерений, линейка.

Описание установки и методика измерений

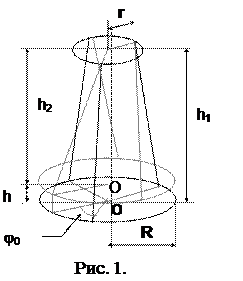
В данной работе для определения момента инерции пользуются методом трифилярного подвеса. Трифилярный подвес представляет собой круглую платформу, подвешенную на трёх симметрично расположенных нитях (рис.1).

Наверху эти нити также прикреплены к диску меньшего, чем у платформы, диаметра. Платформа может совершать крутильные колебания вокруг вертикальной оси. Центр тяжести при этом перемещается по оси вращения. Период колебаний определяется величиной момента инерции платформы. При нагружении платформы период колебаний изменяется, и этим пользуются в данной работе.

Вращаясь в другом направлении, платформа придёт в положение равновесия с кинетической энергией, равной

Пренебрегая работой сил трения, на основании закона сохранения имеем

. (1)

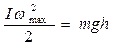
Считая, что платформа совершает гармонические колебания, можно записать зависимость углового смещения платформы от времени в виде

Угловая скорость вращения платформы выразится так

.

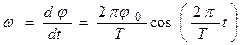
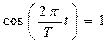
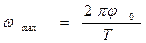
В момент прохождения через положение равновесия ( t = 0; T /2; T ; 3 T /2 и т.д.) и угловая скорость будет максимальной:

. (2)

На основании выражений (1) и (2) имеем

Высота подъёма платформы определяется формулой

. (4)

Подставим в (4) вместо h₁ и h₂ их значения, получим

.

h2

Вследствие малости угла ₀ синус можно заменить аргументом. Тогда получаем

.

h1

(5)

Подставляя (5) в (3), получим

O

R

,

. (6)

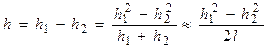
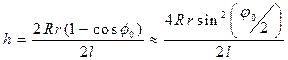
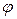
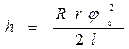
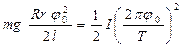
По формуле (6) могут быть определены момент инерции самой платформы и платформы с телом, т.к. все величины в правой части формулы могут быть непосредственно измерены.

Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путём поворота верхнего диска вокруг его оси при помощи натяжения шнура, приводящего в движение рычажок, связанный с диском. Этим и достигается почти полное устранение других некрутильных колебаний, наличие которых вносит погрешность в определение момента инерции.

Порядок выполнения работы

1. Измерить внутренний и внешний диаметры диска. Значения массы диска, его внешний и внутренний радиусы, а также параметры трифилярного подвеса занести в табл. 1.

2. Привести пустую платформу во вращательное движение, измерить время 10 полных колебаний, рассчитать период колебаний. Опыт проделать 3 раза и полученные результаты занести в табл.2.

3. Аналогичные измерения и расчёты сделать для нагруженной платформы.

Номер Опытаt ₀, сnT₀, сt, с NT, с12 …3Ср.

5. Рассчитать теоретическое значение момента инерции:

,

6. Полученные в п. 5 данные сравнить с результатами опыта. Оценить в процентах отклонение значения момента инерции, полученное в опыте, от теоретически рассчитанной величины.

Контрольные вопросы

1. В чём состоит физический смысл момента инерции твёрдого тела?

2. Как рассчитать момент инерции диска относительно оси, проходящей через центр инерции?

3. Как формулируется основной закон динамики вращательного движения?

4. От чего зависит кинетическая энергия вращающегося тела?

5. Как записать закон сохранения механической энергии в условиях данной работы?

6. Как формулируется теорема Штейнера?

7. По какой формуле определяется теоретическое значение момента инерции диска с соосным круглым отверстием?

ОПРЕДЕЛЕНИЕ СКОРОСТИ ПОЛЕТА ПУЛИ

Источник