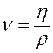Чем обусловлено внутреннее трение в жидкостях
I.6.4 ВНУТРЕННЕЕ ТРЕНИЕ В ЖИДКОСТЯХ
Внутреннее трение возникает в жидкости вследствие взаимодействия молекул. В отличие от внешнего трения, возникающего в месте соприкосновения двух тел, внутреннее трение имеет место внутри движущейся среды между слоями с различными скоростями движения.
При скоростях выше критической скорости слои, близкие к стенкам, заметно отстают вследствие трения от средних, возникают значительные разности скоростей, что влечёт за собой образование вихрей.
Итак, вязкость, или внутреннее трение в жидкостях, обусловливает не только потери энергии на трение, но ещё и новые образования – вихри.
Ньютон установил, что сила вязкости, или внутреннего трения, 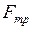
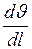
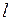
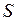
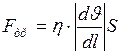
где 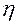
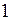
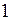
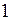
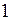
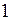
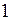
Единица, допускавшаяся к применению до 1980 г.: пуаз (П), по имени французского учёного Пуазейля, который один из первых (1842 г.) начал точные исследования вязкости при течении жидкостей в тонких трубках (соотношение между единицами динамической вязкости: 1 П = 0,1 Па·с)
Пуазейль, наблюдая движение жидкостей в капиллярных трубках, вывел закон, согласно которому:
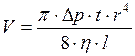
где 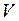
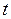
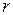
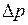
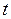
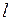
Чем больше вязкость, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причём характер этой зависимости для жидкостей и газов различен:
q динамическая вязкость жидкостей резко уменьшается с повышением температуры;
q динамическая вязкость газов увеличивается с повышением температуры.
Кроме понятия динамической вязкости применяются понятия текучести и кинематической вязкости.
Текучестью 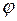
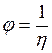
Единица СИ текучести 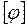
Кинематической вязкостью 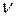
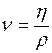
Единица СИ кинематической вязкости 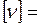
До 1980 г. к применению допускалась единица: стокс (Ст). Соотношение между единицами кинематической вязкости:
1 стокс (Ст) = 10 –4 м 2 /с.
Когда тело шарообразной формы движется в жидкости, ему приходится преодолевать силу трения:
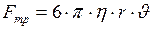
Формула (I.153) представляет собой закон Стокса.
На законе Стокса основано определение вязкости жидкости вискозиметром Гёпплера. В трубу определённого диаметра, заполненную жидкостью, вязкость которой надо определить, опускают шарик и измеряют скорость его падения, которая и является мерой вязкости жидкости.
Английский учёный О. Рейнольдс в 1883 г. в результате своих исследований пришёл к заключению, что критерием характеризующем движение жидкостей и газов, могут служить числа, определяемые безразмерной совокупностью величин, относящихся к данной жидкости и данному её движению. Состав этих отвлечённых чисел, называемых числами Рейнольдса, таков:
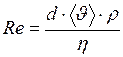
где 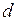
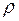
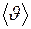
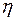
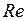
Оказалось, что именно такая совокупность величин, определяющих состояние жидкости или газа, служит надёжной характеристикой их движения. Часто используют другую, более удобную запись числа 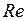
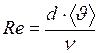
где 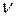
Итак, вычисляя числа Рейнольдса для разных жидкостей и газов, нашли, что переход от ламинарного к турбулентному движению происходит для всех них при определённом значении числа Рейнольдса, именно, если 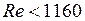
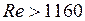
Это условие имеет смысл только тогда, когда обеспечено с самого начала спокойное течение; если же оно механически уже возмущено (например, при падении жидкости из резервуара в трубу), то к его изучению предыдущая теория неприменима.
Дата добавления: 2016-09-06 ; просмотров: 7919 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Явление внутреннего трения (вязкость)



Идеальная жидкость, т.е. жидкость, движущаяся без трения, является абстрактным понятием. Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкость или внутреннее трение. Вязкость (внутреннее трение) наряду с диффузией и теплопроводностью относится к явлениям переноса и наблюдается только в движущихся жидкостях и газах. Вязкость проявляется в том, что возникающее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.
Вязкость (внутреннее трение) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла энергии, затрачиваемой на это перемещение.
Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Молекулярно-кинетическая теория объясняет вязкость движением и взаимодействием молекул.
В жидкостях, где расстояния между молекулами много меньше, чем в газах, вязкость обусловлена в первую очередь межмолекулярным взаимодействием, ограничивающим подвижность молекул. В жидкости молекула может проникнуть в соседний слой лишь при образовании в нём полости, достаточной для перескакивания туда молекулы. На образование полости (на «рыхление» жидкости) расходуется так называемая энергия активации вязкого течения. Энергия активации уменьшается с ростом температуры и понижением давления. В этом состоит одна из причин резкого снижения вязкости жидкостей с повышением температуры и роста её при высоких давлениях. При повышении давления до нескольких тыс. атмосфер вязкость увеличивается в десятки и сотни раз. Строгая теория вязкости жидкостей, в связи с недостаточной разработанностью теории жидкого состояния, ещё не создана.
Вязкость отдельных классов жидкостей и растворов зависит от температуры, давления и химического состава.
Вязкость жидкостей зависит от химической структуры их молекул. В рядах сходных химических соединений (насыщенные углеводороды, спирты, органические кислоты и т.д.) Вязкость изменяется закономерно — возрастает с возрастанием молекулярной массы. Высокая вязкость смазочных масел объясняется наличием в их молекулах циклов. Две жидкости различной вязкости, которые не реагируют друг с другом при смешивании, обладают в смеси средним значением вязкости. Если же при смешивании образуется химическое соединение, то вязкость смеси может быть в десятки раз больше, чем вязкость исходных жидкостей.
Возникновение в жидкостях (дисперсных системах или растворах полимеров) пространственных структур, образуемых сцеплением частиц или макромолекул, вызывает резкое повышение вязкости. При течении «структурированной» жидкости работа внешней силы затрачивается не только на преодоление вязкости, но и на разрушение структуры.
В газах расстояния между молекулами существенно больше радиуса действия молекулярных сил, поэтому Вязкость газов определяется главным образом молекулярным движением. Между движущимися относительно друг друга слоями газа происходит постоянный обмен молекулами, обусловленный их непрерывным хаотическим (тепловым) движением. Переход молекул из одного слоя в соседний, движущийся с иной скоростью, приводит к переносу от слоя к слою определённого импульса. В результате медленные слои ускоряются, а более быстрые замедляются. Работа внешней силы F, уравновешивающей вязкое сопротивление и поддерживающей установившееся течение, полностью переходит в теплоту. Вязкость газа не зависит от его плотности (давления), так как при сжатии газа общее количество молекул, переходящих из слоя в слой, увеличивается, но зато каждая молекула менее глубоко проникает в соседний слой и переносит меньший импульс (закон Максвелла).
Вязкость — важная физико-химическая характеристика веществ. Значение вязкости приходится учитывать при перекачивании жидкостей и газов по трубам (нефтепроводы, газопроводы). Вязкость расплавленных шлаков весьма существенна в доменном и мартеновском процессах. Вязкость расплавленного стекла определяет процесс его выработки. По вязкости во многих случаях судят о готовности или качестве продуктов или полупродуктов производства, поскольку вязкость тесно связана со структурой вещества и отражает те физико-химические изменения материала, которые происходят во время технологических процессов. Вязкость масел имеет большое значение для расчёта смазки машин и механизмов и т.д.
Прибор для измерения вязкости называется вискозиметром.
Савельев И.В. Курс общей физики, том I

Загрузить всю книгу 
Титульный лист
Главная редакция физико-математической литературы
Механика, колебания и волны,
КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I
Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.
Предисловие к четвертому изданию
При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.
Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.
Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.
Ноябрь 1969 г. И. Савельев
Из предисловия к четвертому изданию
Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.
При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.
Коэффициент внутреннего трения или вязкость жидкости



Параметр вязкости выступает одним из основных свойств определяющих характер движения жидкости.
Если текущая жидкость соприкасается с неподвижной поверхностью (например при движении жидкости в трубке) то слой такой жидкости перемещается с различными скоростями. В результате между этими слоями возникает напряжение сдвига: более быстрый слой стремится вытянуться в продольном направлении, а более медленный задерживает его.
Наличие вязкости приводит к рассеиванию (диссипации) энергии внешнего источника, вызывающего движение жидкости, и переходу ее в теплоту. Жидкость без вязкости (так называемая идеальная жидкость) является абстракцией. Всем реальным жидкостям присуща вязкость.
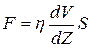
Таким образом сила внутреннего трения тормозит более быстрые слои и ускоряет более медленные слои. Наряду с коэффициентом динамической вязкости рассматривают так называемый коэффициент кинематической вязкости
Жидкости делятся по вязким свойствам на два вида: ньютоновские и неньютоновские.
Ньютоновской называется жидкость, коэффициент вязкости которой зависит только от ее природы и температуры. Для ньютоновских жидкостей сила вязкости прямо пропорциональна градиенту скорости. Для них непосредственно справедлива формула Ньютона (9.1), коэффициент вязкости в которой является постоянным параметром, не зависящим от условий течения жидкости.
Неньютоновской называется жидкость, коэффициент вязкости которой зависит не только от природы вещества и температуры, но также и от условий течения жидкости, в частности от градиента скорости. Коэффициент вязкости в этом случае не является константой вещества. При этом вязкость жидкости характеризуют условным коэффициентом вязкости, который относится к определенным условиям течения жидкости (например, давление, скорость). Зависимость силы вязкости от градиента скорости становится нелинейной:
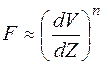
где n характеризует механические свойства при данных условиях течения.
Примером неньютоновских жидкостей являются суспензии. Если имеется жидкость, в которой равномерно распределены твердые невзаимодействующие частицы, то такую среду можно рассматривать как однородную, т.е. мы интересуемся явлениями, характеризующимися расстояниями, большими по сравнению с размером частиц. Свойства такой среды в первую очередь зависят от вязкости жидкости. Система же в целом будет обладать уже другой, большей вязкостью h¢ зависящей от формы и концентрации частиц. Для случая малых концентраций частиц С справедлива формула:
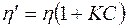
Если структура частиц изменится (например, при изменении условий течения), то и коэффициент К в (9.2), а следовательно, и вязкость такой суспензии h’ также изменится. Подобная суспензия представляет собой неньютоновскую жидкость. Увеличение вязкости всей системы связано с тем, что работа внешней силы при течении суспензий затрачивается не только на преодоление истинной (неньютоновской) вязкости, обусловленной межмолекулярным взаимодействием в жидкости, но и на преодоление взаимодействия между ней и структурными элементами.
Условия образования агрегатов различны в крупных и мелких сосудах. Это связано в первую очередь с соотношением размеров сосуда, агрегата и эритроцита характерные размеры dэр=8 мкм, dагр»10dэр:
1. Крупные сосуды (аорта, артерии):
Диаметр сосуда больше диаметра агрегата и значительно диаметра эритроцита. При этом градиент скорости сдвига небольшой, эритроциты собираются в агрегаты в виде монетных столбиков. В этом случае вязкость крови h = 0,005 Па • с.
2. Мелкие сосуды (мелкие артерии, артериолы):
Диаметр сосуда меньше диаметра агрегата и больше в 5–20 диаметра эритроцита
В них градиент скорости сдвига значительно увеличивается и агрегаты распадаются на отдельные эритроциты, тем самым уменьшая вязкость системы. Для этих сосудов чем меньше диаметр просвета, тем меньше вязкость крови. В сосудах диаметром около 5 d эр вязкость крови составляет примерно 2/3 вязкости крови в крупных сосудах.
3. Микрососуды (капилляры):
Диаметр сосуда меньше диаметра эритроцита
В живом сосуде эритроциты легко деформируются, становясь похожими на купол, и проходят, не разрушаясь, через капилляры даже диаметром 3 мкм. В результате поверхность соприкосновения эритроцитов со стенкой капилляра увеличивается по сравнению с недеформированным эритроцитом, способствуя обменным процессам.
Для описания процессов в микрососудах формула (9.2) не применима, так как в этом случае не выполняются допущения об однородности среды и твердости частиц.
Таким образом, внутренняя структура крови, а следовательно, и ее вязкость (9.2), оказывается неодинаковой вдоль кровеносного русла в зависимости от условий течения. Кровь является неньютоновской жидкостью. Зависимость силы вязкости от градиента скорости для течения крови по сосудам не подчиняется формуле Ньютона (9.1) и является нелинейной.
Как и у любой жидкости, вязкость крови возрастает при снижении температуры. Например, при уменьшении температуры с 37° до 17° вязкость крови возрастает на 10 %.
Жидкостное трение
Типичным примером является шарик, который падает в вязкую жидкость : чем быстрее он движется, тем больше сила трения жидкости, действующая на него (поскольку она пропорциональна скорости), до тех пор, пока любой из них не достигнет режима равновесия, при котором сила трения Архимедова тяга и сила тяжести точно компенсируют друг друга: тогда скорость шара становится постоянной (по закону Стокса ).
Трение жидкости возникает во множестве повседневных проблем: падение давления в трубопроводе, трение воздуха о автомобиль, трение воды о корпус лодки.
Существуют относительно простые формулы, применимые в некоторых основных случаях. Однако, как только геометрия объекта, погруженного в жидкость, становится более сложной, необходимо прибегать к численным расчетам CFD или к физическим испытаниям (например, с использованием аэродинамической трубы).
Резюме
Глобальные выражения сил жидкостного трения
На малой скорости
Когда число Рейнольдса очень мало по сравнению с 1, поток находится в ламинарном режиме. Прохождение жидкости не вызывает турбулентности. В этой ситуации разрешение уравнений Навье-Стокса генерирует выражение сил гидравлического трения, пропорционального скорости.
Например, в случае шара, медленно движущегося в жидкости, мы получаем знаменитое уравнение Стокса :
где мы можем идентифицировать K как равное:
Поскольку сопротивление шара пропорционально его характерной длине, а также скорости жидкости, можно обратиться к размерному коэффициенту сопротивления Лэмба (как его называет Здравкович), этот размерный коэффициент также можно назвать « линейным» ( в отличие от квадратичной, которая важна для самых сильных Рейнольдсов, как описано ниже). ПРОТИВ Икс <\ displaystyle C_ 
Чтобы узнать линейность любого объекта, необходимо провести измерение на подходящем испытательном стенде. Также можно выполнять математические или численные расчеты с помощью специального программного обеспечения (см. По этому вопросу специализированную статью Стокса, в которой приводится линейное значение определенного количества тел). ПРОТИВ Икс <\ displaystyle C_ 
На умеренной скорости
Когда число Рейнольдса составляет от 30 до 800, поток находится в промежуточном состоянии, на полпути между ламинарным и турбулентным потоком. В этом интервале уравнения Навье-Стокса можно упростить (при определенных предположениях), чтобы получить обычно используемую формулу:
Для примера со сферой мы имеем:
На высокой скорости
Во всем диапазоне чисел Рейнольдса для сферы
В качестве примера можно представить квадратичный (или квадратичный) коэффициент сопротивления сферы во всем диапазоне возможных чисел Рейнольдса, хотя этот квадратичный коэффициент не имеет физического значения при очень низких значениях Рейнольдса. ПРОТИВ Икс <\ displaystyle C_ 
Локальное выражение сил жидкостного трения.
Определение
Случай ньютоновских жидкостей
Сила трения жидкости, оказываемая одним слоем жидкости ( ньютоновским ) на другой слой или ньютоновской жидкостью на твердой стенке, локально выражается в форме силы на единицу площади:
Вышеупомянутая производная берется в точке на поверхности. Когда мы имеем дело с твердой стенкой, нас интересует относительная скорость жидкости, и стенка исчезает в точке контакта.
Неньютоновские жидкости
Пример применения в точечной механике
(Общая) сила трения, действующая на движущийся твердый объект (относительно окружающей жидкости), является результатом (местных) сил трения, действующих во всех точках его поверхности, контактирующих с жидкостью.
Общая сила трения зависит от скорости твердого тела (относительно жидкости на большом расстоянии от стенок). В случае ньютоновской жидкости :
Пример гидравлического трения, пропорционального скорости
Уравнение, описывающее перемещение шара, задается фундаментальным принципом динамики :
которое решается как дифференциальное уравнение первого порядка с постоянными коэффициентами и вторым членом, решение которого записывается
взяв в качестве начального условия нулевую скорость (при t = 0). Эта скорость очень отрицательная, так как мяч падает.
По прошествии определенного времени ( t
5 м / k ) скорость стремится к постоянному значению (предельной скорости), определяемому
Таким образом, уравнение можно записать:
Нагрев за счет сверхзвуковых и гиперзвуковых потоков
Как мы знаем, вход в атмосферу природных объектов (метеоров) или созданных руками человека (космических кораблей) всегда происходит с большим выделением тепла (что имеет положительный эффект, заключающийся в значительном уменьшении кинетической энергии этих тел., Следовательно, для их замедления. вниз). Однако, как это ни парадоксально, это большое тепловыделение не связано с усиленным нагревом пограничного слоя, окружающего тело (т. Е. Трением воздуха о его поверхность). Этот нагрев происходит в основном из-за быстрого сжатия воздуха в передней части тела.