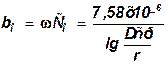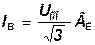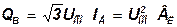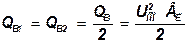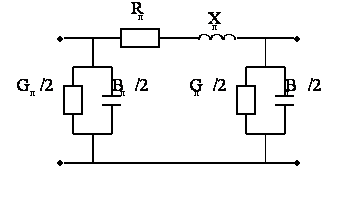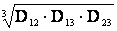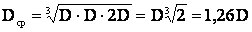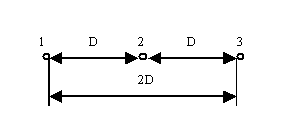Чем обусловлена емкостная проводимость лэп

АКТИВНАЯ И ЕМКОСТНАЯ ПРОВОДИМОСТИ ЛИНИЙ ЭЛЕКТРИЧЕСКОЙ СЕТИ

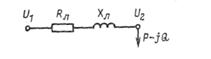
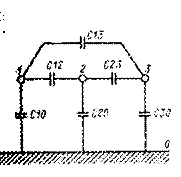
Под действием электростатического поля возникающего между фазовыми проводами линий, а также между этими проводами и землей, в диэлектрике, окружаю­щем токоведущие элементы воздушных или кабельных линий возникают токи смещения. В линиях переменного тока эти токи имеют синусоидальный характер.

Рис. 2.10. Схема замещения линии напряжением 6—35 кВ

Линии более высоких напряжений (110 кВ и выше, рис. 2.11) имеют, как правило, большую протяженность и обла­дают помимо активного и индуктивного сопротивлений еще и активной G_л и реактивной В_л проводимостями, которые необходимо учитывать при расчете этих линий.

Активная проводимость линии G_л обусловлена активны­ми потерями на корону. Коронирование проводов приводит к ряду нежелательных последствий: снижению к. п. д., усиленному окислению поверхности проводов, появлению радиопомех. Поэтому для сооружения воздушных линий применяют только такие провода, диа­метр которых при том или ином номинальном напряжении определяет меньшую напряженность поля, нежели это требуется для заметного развития короны. Увеличение внешнего
диаметра провода сверх предельных значений, позволяет не считаться с короной при расчетах электрических сетей и учитывать соответствующих потерь мощности в расчетных схемах. Одним из факторов, влияющих на уменьшение потерь от короны, является увеличение сечения провода воздуш­ной линии. Поэтому при выборе проводов воздушных линий напряжением 110 кВ и выше из условия допустимых по­терь на корону следует принимать сечения не ниже: АС70—110 кВ; АС120—154 кВ; АС240—220 кВ; АС600—330 кВ.

Приняв указанные минимальные сечения линии, при ко­торых потери на корону будут отсутствовать, т.е. G_л =0, Упрощаем П-образную схему замещения линии (см. рис.2.11б)

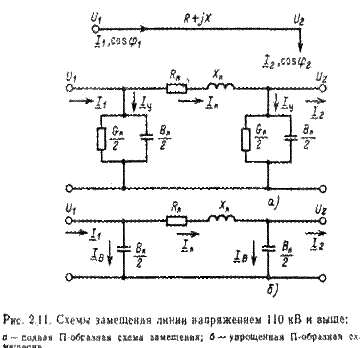
В воздушных линиях переменные токи смешения (зарядные токи линии) практически не имеют активной составляющей, так как потери, связан­ные с переориентацией диполей диэлектрика (в данном случае, воздуха), ничтожно малы. Величина зарядного тока опреде­ляется рабочей емкостью линии, которой отвечает емкостная проводимость b₀ (1/Ом*км),которую можно рассматривать как конденсатор с соответствующей емкостью (рис. 2.12,а, б). Под действием приложенного к линии переменного напряжения в емкости линии возникает переменное электрическое полеи соответственно емкостный переменный ток, называется зарядным током линии I_В. Зарядный ток ц_а единицу длины линии при равномерно распределенной емкости (b₀ =const) зависит от напряжения в каждой точке линии. Обычно принимают вдоль всей длины линии среднее напряжение, равное номинальному напряжению сети U_ном.

Емкостный ток, как видно из рис. 2.13, изменяется вдоль линии пропорционально длине линии. Зарядный ток зави­сит от емкостной проводимости линии В_л.

В расчетах сетей рабочую емкость трехфазной воздушной линии, отнесенную к 1 км длины линии, Ф/км, можно определить:

где D_cp — среднее геометрическое расстояние между проводами, см;

r=d/2 — внешний радиус провода (кабеля),

Емкостная проводимость 1 км В Л и КЛ с учетом (2.42), См (сименс, обратная величина сопротивления)/км

Рис. 2.12. Емкостные проводимости трехфазных линий электропередачи: а —воздушные линии; б — кабельные линии

Рис. 2.13. Изменение емкостного тока по длине линии

Где ω= 2πf=314 Гц –угловая частота переменного тока.

Ёмкостная проводимость линии, См, длиной l, км,

Зарядный ток линии, кА,

При П-образной схеме замещения линии (рис. 2.11, а и б) вся емкостная проводимость линии условно сосредото­чена по концам схемы и, следовательно, проводимость на концах схемы замещения равна В_Л /2.

Емкостная (зарядная) мощность линии, Мвар, с уче­том (2.45)

где Uном — номинальное линейное напряжение линии, кВ. Зарядная мощность, Мвар, по концам П-образной схе­мы замещения линии

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Схемы замещения, параметры воздушных и кабельных линий

Характеристики и параметры элементов электрической сети

В большинстве случаев можно считать, что параметры линии электропередачи (активное и реактивное сопротивление, активная и емкостная проводимости) равномерно распределены по ее длине. Для линий сравнительно небольшой длины распределенность параметров можно не учитывать и использовать рассредоточенные параметры: активное и реактивное сопротивление линии R и Х, и реактивную проводимости G и В.

Воздушные линии электропередачи напряжением 110 кВ и выше длиной до 300-400 км обычно представляются П – образной схемой замещения.

Активное сопротивление проводов и кабелей определяется материалом токоведущих жил и их сечениями. Погонное активное сопротивление (на 1 км длинны) для голых проводов и кабелей при температуре +20°С определяется

r= (3.1)

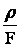
Активное сопротивление линии, длиной l определяется

Активное сопротивление проводов и кабелей при частоте 50 Гц примерно равно омическому сопротивлению. При этом не учитывается влияние поверхностного эффекта. Пренебрегают также тем влиянием, которое оказывают на величину активного сопротивления колебания температуры проводника, и используют в расчетах величины этих сопротивлений при средних температурах (+20°С).

Реактивное сопротивление. Переменный ток, проходя по линии, образует вокруг проводников переменное магнитное поле, которое наводит в про-

воднике электродвижущую силу (э.д.с.) обратного направления – э.д.с. самоиндукции. При данном токе в проводе и отсутствии активного сопротивления в нем э.д.с. самоиндукции полностью уравновешивает приложенное напряжение

I×w×L=U

где L – коэффициент самоиндукции провода.

Сопротивление току, обусловленное противодействием э.д.с. самоиндукции, называется индуктивным сопротивлением. Соседние провода трехфазной линии, являющиеся обратными проводами для тока рассматриваемого провода, в свою очередь наводят в нем э.д.с. согласно с основным током направления, что уменьшает э.д.с. самоиндукции и соответственно реактивное сопротивление. Поэтому, чем дальше друг от друга расположены фазные провода линии, тем влияние соседних проводов будет меньше, а поток рассеяния между проводами и, следовательно, индуктивное сопротивление линии – больше.

На индуктивное сопротивление оказывают влияние также диаметр провода, магнитная проницаемость провода и частота переменного тока.

Величина погонного индуктивного сопротивления линии определяется

х= w×(4,6×lg + 0,5m)×10 (3.2)

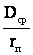
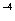
Для проводов из цветного металла (μ=1) при промышленной частоте 50 Гц формула (4.2) примет вид

Среднегеометрическое расстояние между проводами одноцепной трехфазной линии

D=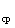

При расположении проводов по вариантам равностороннего треугольника все провода находятся на одинаковом расстоянии относительно друг друга, и среднегеометрическое расстояние D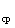=D (см.рисунок 3.2).

При горизонтальном расположении проводов (см.рисунок 3.3).

На линиях 330 кВ и выше применяются расщепленные провода. На таких линиях каждая фаза имеет не один, а несколько проводов. Это приводит к увеличению радиуса фазы, который определяется по выражению

(3.4)

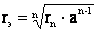
где 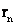— радиус отдельных проводов, входящих в расщепленную фазу линии;

Индуктивное сопротивление линии с расщепленными проводами

.

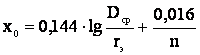
Для линии длиной l индуктивное сопротивление

.

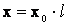
Активная проводимость линий обусловлена потерями активной мощности от токов утечки через изоляцию и от электрической короны на проводах.

Потери электрической энергии от токов утечки через изоляцию возникают при включении линии электропередачи под напряжение. Эти потери незначительны в кабельных и очень малы в воздушных линиях, значит и небольшая активная проводимость.

Потери на корону более значительны. Они связаны с ионизацией воздуха около проводов и возникают, когда напряженность электрического поля у поверхности провода превышает электрическую прочность воздуха. В этом слу-

чае на поверхности провода образуются электрические разряды. Из-за неровностей верхнего повива многопроволочных проводов, загрязнений и заусениц разряды появляются вначале только в отдельных точках провода. Это так называемая местная корона провода. По мере повышения напряжения корона распространяется на большую поверхность провода и в конечном счете охватывает провод целиком по всей его длине, т.е. возникает общая корона.

Кроме потерь электроэнергии, корона вызывает коррозию проводов, арматуры гирлянд изоляторов, оказывает мешающее воздействие на работу высокочастотных каналов связи линий электропередачи и вызывает высокочастотные помехи в проводных линиях связи и радиопомехи.

Если утечкой в линиях пренебречь, то активная проводимость, обусловленная короной определяется

(3.5)

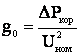
где 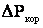— потери мощности на корону, кВт/км;

Основными мерами по снижению потерь на корону является увеличение сечений проводов, расщепление или применение полых проводов.

Реактивная проводимость обусловлена наличием емкости между проводами и землей и имеет емкостной характер. Она определяется известным выражением.

b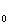=w×С

Рабочая емкость линии зависит от диаметра проводов, их взаимного расположения, расстояния между ними и диэлектрической проницаемости среды.

В практических расчетах электрических сетей рабочую емкость трехфазной воздушной линии с одним проводом на фазу определяют по формуле

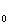
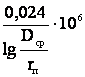
С=. (3.6)

При частоте переменного тока 50 Гц

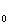
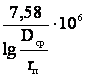
b=. (3.7)

Емкостная проводимость всей линии

B = b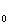×l.

Зарядный ток линии. Под действием приложенного к линии переменного напряжения в емкости линии возникает переменное электрическое поле и возникает реактивный ток. Этот ток называется емкостным или зарядным током линии.

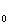
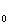
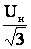
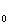
I×b=U×b=b. (3.8)

Зная емкостной ток линии, легко определить емкостную или зарядную мощность линии.

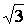
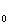
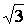
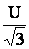
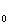
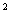
Q_b= ×U×I×b= ×U××b= U×b (3.9)

где U – рабочее линейное напряжение, кВ.

Кабельные линии электропередачи представляются такой же П-образной схемой замещения, что и воздушные линии. Погонные активные и реактивные сопротивления r и x определяют по справочным таблицам, так же как и для воздушных. Из выражений (3.3) и (3.7) видно, что х уменьшается, b растет при сближении фазных проводов. Для кабельных линий расстояние между фазами значительно меньше, чем для воздушных и х очень мало. При расчетах режимов для кабельных сетей напряжением 10 кВ и ниже можно учитывать только активное сопротивление. Емкостной ток и зарядная мощность в кабельных линиях больше, чем в воздушных. В кабельных линиях высокого напряжения учитывают Q. Активную проводимость G учитывают для кабелей 110 кВ и выше.

Источник

Активная и реактивная проводимости воздушных и кабельных линий.

Проводимость, расчет электрических цепей методом проводимостей

Для расчета сложных электрических цепей, и в особенности цепей переменного тока, целесообразно вместо сопротивления использовать проводимость.

Проводимость в цепи постоянного тока

— величина, обратная сопротивлению

В цепях переменного тока, как известно, существует три типа сопротивлений: активное

Для введения активной

и реактивной проводимостей рассмотрим цепь переменного тока из последовательно соединенных активного и индуктивного сопротивлений (рис. 10.4 а).

Построим для нее векторную диаграмму (рис. 10.4 6). Ток в цепи

разложим на активную и реактивную составляющие и от полученного треугольника токов перейдем к треугольнику сопротивлении (рис. 10.4 в). Из последнего имеем:

где — активная проводимость,

где — реактивная проводимость.

Теперь установим взаимосвязь между проводимостями. Для рассматриваемой цепи имеем:

где — полная проводимость цепи.

По аналогии с треугольником сопротивлений (рис. 10.5 в) строим треугольник проводимостей (рис. 10.5 г). По аналогии с индуктивным

и емкостным сопротивлениями различают индуктивную и емкостную проводимости.

Если в цепи больше двух параллельных ветвей, то для рационального расчета используется метод проводимостей, который основан на следующем.

1)Ток в каждой цепи является векторной суммой активной и реактивной составляющих (рис. 10.5).

Например, для рассмотренной выше цепи действующие значения токов в ветвях можно рассчитать по следующим формулам:

2) Активные составляющие совпадают по фазе с напряжением и равны:

и — активные проводимости первой и второй ветвей.

3) Реактивные составляющие токов отличаются по фазе от напряжения на и рассчитываются по формулам:

и — реактивные проводимости первой и второй ветвей. Тогда: где и — полные проводимости обоих ветвей.

Проводимость всей цепи может быть рассчитана по формуле представлена треугольником проводимостей (рис.3.28г), который является следствием векторной диаграммы токов:

4)Общая сила тока в цепи может быть рассчитана как модуль векторной суммы активной и реактивной составляющих

5)Сдвиг фаз между током и напряжением:

6)Активную, реактивную и полную мощность цепи можно рассчитать по формулам:

0.3 Взаимная индуктивность. Согласное, встречное включения катушек

Поток самоиндукции первой катушки

Полное потокосцепление первой катушки:

и направлены одинаково, говорят «согласно». Поэтому в скобках перед стоит (+).

Если изменить направление тока в катушке 2, то потоки будут направлены встречно и будет знак(-). В общем случае:

— индуктивность первой катушки; — взаимная индуктивность. Аналогично для второй катушки:

Полная ЭДС, индуктированная в первом контуре:

Явление наведения ЭДС в каком-либо контуре при изменение тока в другом контуре, называется взаимоиндукцией.

Наведённую ЭДС называют ЭДС взаимоиндукции и обозначают:

— ЭДС взаимоиндукции в первой катушке,

— ЭДС взаимоиндукции во второй катушке.

Степени индуктивной связи катушки определяются с помощью коэффициентов связи:

При расчёте таких цепей необходимо учитывать, как направлены потоки маг-нитносвязанных катушек — согласно или встречно.

Направления потоков можно определить, зная направление намотки катушек на сердечнике и направление тока в катушках (рис. 10.7).

Токи, входящие в одноимённые зажимы магнитосвязанных катушек, дают согласное направление магнитных потоков в этих катушек.

Одноимённые зажимы помечают либо точкой, либо звёздочкой. Если на принципиальной электрической схеме токи ориентированы одинаково относительно одноимённых зажимов катушек, то это согласное включение катушек, иначе — встречное.

Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):

Возможно эти страницы вам будут полезны:

Особенности активного сопротивления

В общем виде данный параметр выглядит, как противодействие определенного участка цепи проходящему по нему току. Полученная в результате такого процесса величина участвует в преобразовании энергии и ее переходе в какое-то другое состояние.

Важно! Это явление наблюдается исключительно в ситуациях с переменным током. Только он способен образовывать в кабелях оба вида противодействия.

Величина активного сопротивления обусловлена эффектом поверхностного типа. Наблюдается процесс своеобразного перемещения тока от центра к поверхности проводника. Сечение кабеля используется не полностью, а возникающее противодействие будет значительно превышать аналогичный омический показатель.

Обратим внимание на такой момент:

Удельная проводимость

Удельной проводимостью (удельной электропроводностью) называют меру способности вещества проводить электрический ток. Согласно закону Ома в линейном изотропном веществе удельная проводимость является коэффициентом пропорциональности между плотностью возникающего тока и величиной электрического поля в среде:

В неоднородной среде σ может зависеть (и в общем случае зависит) от координат, то есть не совпадает в различных точках проводника.

Удельная проводимость анизотропных (в отличие от изотропных) сред является, вообще говоря, не скаляром, а тензором (симметричным тензором ранга 2), и умножение на него сводится к матричному умножению:

Емкостное и индуктивное сопротивление в цепи переменного тока

Если мы включим конденсатор в цепь постоянного тока, то обнаружим, что он оказывает бесконечно большое сопротивление, поскольку постоянный ток просто не может пройти через диэлектрик между обкладками, так как диэлектрик по определению не проводит постоянный электрический ток.

Конденсатор разрывает цепь постоянного тока. Но если тот же конденсатор включить теперь в цепь переменного тока, то окажется, что ее конденсатор будто бы и не разрывает полностью, он просто попеременно заряжается и разряжается, то есть электрический заряд движется, и ток во внешней цепи поддерживается.

Опираясь на теорию Максвелла, в этом случае можно сказать, что переменный ток проводимости внутри конденсатора все же замыкается, только в данном случае — током смещения. Значит конденсатор в цепи переменного тока выступает неким сопротивлением конечной величины. Такое сопротивление называется емкостным

Практика давно показала, что величина переменного тока, текущего через провод, зависит от формы этого провода и от магнитных свойств среды вокруг него. При прямом проводе ток будет наибольшим, а если этот же провод свернуть в катушку с большим количеством витков, то величина тока окажется меньше.

А если в ту же катушку еще и ввести ферромагнитный сердечник, то ток еще сильнее уменьшится. Следовательно проводник оказывает переменному току не только омическое (активное) сопротивление, но еще и некое дополнительное сопротивление, зависящее от индуктивности проводника. Данное сопротивление называется индуктивным

Принцип действия индуктивного сопротивления линий

Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.

Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.

Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение

Плотность тока смещения

В классической электродинамике существует понятие тока смещения, который пропорционально равен быстроте изменения индукции электрического поля. Он не связан с перемещением каких-либо частиц поэтому, по сути, не является электрическим током. Несмотря на то, что природа этих токов разная, единица измерения плотности у них одинаковая — A/м 2

Ток смещения – это поток вектора быстроты изменения электрического поля ∂E/∂t

через
S
— некоторую поверхность. Формула тока смещения выглядит так:

— скорость изменения электрического поля [Н/(Кл·с)]

– площадь поверхности [м 2 ]

Плотность тока смещения определяется по следующей формуле:

— скорость изменения электрического поля [Н/(Кл·с)]

— скорость изменения вектора эл. индукции [Кл/м 2 ·с)]

ВОЗДУШНЫЕ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ

Воздушные линии электропередачи напряжением 110 кВ и выше при длине до 300 — 400 км обычно представляются П-образной схемой замещения (рис. 2.1).

Активное сопротивление определяется по формуле

– удельное сопротивление, Ом/км (при температуре провода +20оС);

Для электрических сетей, выполненных из цветного металла, при частоте fс

= 50 Гц влияние поверхностного эффекта очень незначительно. Поэтому в расчётах таких сетей активное сопротивление проводов принимают равным их омическому сопротивлению (или сопротивлению постоянному току).

Определение активного сопротивления стальных проводов, применяемых для сетей переменного тока, поскольку эти провода представляют собою ферромагнитный материал, отличается от расчётов сопротивления проводов из цветного металла.

Активное удельное сопротивление для сталеалюминиевых проводов определяется по таблицам в зависимости от поперечного сечения. При температуре провода, отличной от +20°С, сопротивление линии уточняется по известным из курса “Электротехнические материалы” формулам.

Реактивное сопротивление определяется следующим образом

– удельное реактивное сопротивление, Ом/км.

Это сопротивление обусловлено переменным магнитным полем, возникающим вокруг проводов линии электропередачи при протекании по ним переменного тока.

Чем больше расстояние между проводами и меньше диаметр провода, тем больше индуктивное сопротивление линии.

Удельные индуктивные сопротивления фаз воздушной линии в общем случае различны. При расчетах симметричных режимов используют среднее значение x0:

– среднегеометрическое расстояние между фазами, определяемое соотношением

– расстояния между проводами соответствующих фаз “a”, “b”, “с”.

Для наиболее распространенных способов расположения фаз характерно одно из двух (рис. 2.2) их размещений.

При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Отличие хо

одной цепи при учёте и не учете влияния другой цепи не превышает 6 % и не учитывается при практических расчётах.

В ЛЭП при Uн ≥ 330 кВ

провод каждой фазы расщепляется на несколько проводов, что соответствует увеличению эквивалентного радиуса провода.

В выражении (2.2) вместо rпр используется

– эквивалентный радиус провода;

– среднеарифметическое расстояние между проводами одной фазы;

– число проводов в одной фазе.

Для линии с расщеплёнными проводами последнее слагаемое в (2.2) уменьшается в “nф

Активное удельное сопротивление расщеплённой фазы определяется так:

– удельное сопротивление провода данного сечения, определённое по справочным таблицам.

Для сталеалюминиевых проводов хо определяется по справочным таблицам в зависимости от сечения, для стальных – в зависимости от сечения и тока.

Интересно отметить, что расщепление проводов фаз в России впервые было применено в пятидесятые годы на ЛЭП Самара – Москва, в каждой фазе которой подвешены три провода марки АСО – 480 с расстоянием между проводами 400 мм. Это позволило снизить индуктивное сопротивление приблизительно на (25-30)%.

Активная проводимость соответствует двум видам потерь мощности: от тока утечки через изоляторы и на корону.

Токи утечки через изоляторы малы и потерями мощности в них можно пренебречь.

Явление короны заключается в том, что, если напряжённость электрического поля вокруг проводов вследствие приложенного к ним напряжения превышает величину электрической прочности воздуха, равную 21,2 кВ/см (2,12 кВ/мм) при температуре +25оС, нормальных давлении и влажности, то вокруг проводов возникает ионизация воздуха, проявляющаяся в виде фиолетового свечения, характерного шипящего треска и сопровождающееся запахом озона.

Ионизация воздуха (явление короны) связано с потерями активной мощности. Напряжение, при котором возникают потери на корону, называются коронным или критическим напряжением короны.

Критическое фазное напряжение короны равно:

Uкр,ф = 48,9 · mo · mn × δ × r · lg

– коэффициент, учитывающий состояние поверхности провода; для одно-проволочных проводов
mo = 0,93…0,98
, а для многопроволочных
mo = 0,83…0,87
;

– коэффициент, учитывающий состояние погоды; при сухой и ясной погоде
mn = 1
; при плохой погоде (туман, иней, гололёд, дождь, снежная буря)
mn = 0,8
;

— коэффициент, учитывающий атмосферное давление
“в”
и температуру воздуха
υ
; при
в
= 76
см. рт. ст
. и
υ = 25оС
коэффициент
δ = 1
;

– наружный диаметр провода (см) (определяется по стандарту на провода);

– расстояние между осями проводов (см).

Критическое междуфазное напряжение короны

Потери на корону наступают при совпадении напряжения линии с критическим напряжением короны и возрастают по мере увеличения напряжения сверх критического.

Поэтому для выяснения, будет ли в данной ЛЭП потеря мощности на корону, необходимо подсчитать величину критического напряжения короны и сравнить её с величиной рабочего напряжения линии U

Из (2.5) следует, что наиболее радикальным средством снижения потерь мощности на корону (по существу, на исключение короны) является увеличение радиуса провода “r

Как уже отмечалось, при U ≥ 330 кВ

практикуется расщепление провода каждой фазы на несколько проводов, что соответствует увеличению эквивалентного радиуса провода.

Как следствие, согласно (2.5), этот приём вызывает увеличение напряжения короны и в соответствии с (2.7) приводит к уменьшению потерь мощности на корону. Эти потери имеют достаточно высокий уровень. В частности, для нерасщеплённых проводов на ВЛ 330 кВ потери достигают 2-4 кВт/км, а на ВЛ 750 кВ (даже при расщеплении фазы на пять проводов) уровень потерь на корону 9-16 кВт/км.

Что касается расстояния между проводами “D

”, то, входя под знак логарифма, оно влияет на коронное напряжение незначительно. Физически это объясняется тем, что при увеличении диаметра провода плотность электрического поля у поверхности провода уменьшается в гораздо большей степени, чем от увеличения расстояния между проводами.

К тому же увеличение расстояния между проводами значительно повышает стоимость ЛЭП и для снижения потерь на корону не применяется.

Величина потерь активной мощности на корону во всех трёх фазах при напряжении U

с частотой
fc = 50 Гц
определяется по эмпирической формуле

Активная проводимость, отнесённая к 1км длины линии, может быть найдена из выражения

Формулы (2.5) и (2.7) для определения Uкр,ф

и
DРк
справедливы для ЛЭП с расположением проводов трёхфазной линии в вершинах равностороннего треугольника.

При расположении проводов в одной плоскости корона на среднем проводе наступает при напряжении на 4% меньшем, а на крайних — на 6% большем, чем Uкр

, подсчитанное по (2.5) для расположения проводов в вершинах равностороннего треугольника. Явление короны недопустимо в ЛЭП не только из-за потерь мощности, которые при определённых условиях могут достигать ощутимых значений, но и из-за вызываемых этим явлением коррозии проводов, радиопомех и вредного влияния на провода связи (здесь можно предположить и наличие проводной связи с использованием проводов самой ЛЭП, полагая, в частности, диспетчерскую связь через провода ЛЭП).

В практике проектирования электрических сетей с U ≤ 220 кВ

потери на корону не учитываются. В сетях с
U > 330 кВ
определение потерь мощности при расчёте оптимальных режимов включает в себя и расчёт потерь на корону.

Ёмкостная проводимость линии обусловлена наличием частичных емкостей у каждого из проводов линии как к другим проводам, так и к земле (рис. 2.3).

Рабочая ёмкость провода составляется из частичных ёмкостей и представляет собой отношение всего количества электричества, соответствующего всем силовым линиям, исходящим от данного провода, к другим проводам и к земле, к потенциалу этого провода или, короче говоря, отношение заряда данного провода к его потенциалу. Понятие рабочей ёмкости справедливо лишь для симметричной системы, какой является трёхфазная ЛЭП с расположением проводов в вершинах равностороннего треугольника при достаточной удалённости проводов от земли.

В несимметричной трёхфазной ЛЭП понятием рабочей ёмкости можно пользоваться лишь при условии, что на линии осуществлён полный цикл транспозиции проводов. При этом влиянием на ёмкость земли, соседних проводов и тросов пренебрегают.

Эти допущения дают погрешность в определении рабочей ёмкости воздушных трёхфазных линий в наиболее неблагоприятном случае не более 5 %, что в большинстве случаев допустимо.

В практических расчётах ёмкость воздушной трехфазной линии определяется по формуле:

и
r
– соответственно среднее расстояние между осями проводов и радиус провода.

Ёмкостная проводимость линии “bл

”, обусловленная ёмкостями между проводами разных фаз и ёмкостью провод-земля, определяется следующим образом

— удельная ёмкостная проводимость, См/км;

” находится по справочным таблицам, либо по формуле

Наличие ёмкости проводов вызывает в линии ток, создаваемый приложенным к линии переменным напряжением и соответственно переменным электрическим полем, под влиянием которого происходит перемещение электрических зарядов. Этот ток называется емкостным или зарядным током линии.

Численно удельный ёмкостный – реактивный – ток может быть определён по формуле

– междуфазное напряжение, В.

Величина ёмкостного тока на единицу длины при равномерно распределённой ёмкости (bо = const)

зависит от величины напряжения в каждой точке линии и поскольку напряжение меняется вдоль линии по величине и по фазе, то также по величине и фазе меняется и ёмкостной ток.

Однако в практических расчётах этим обстоятельством обычно пренебрегают и вместо действительного напряжения принимают номинальное напряжение сети. Ёмкостный ток в начале линии состоит из суммы единичных ёмкостных токов и поэтому ёмкостный ток возрастает от конца к началу линии пропорционально длине линии.

Ток же, обусловленный нагрузкой, не зависит от длины линии. Так как суммарный ток линии определяется геометрическим сложением в каждой точке линии тока нагрузки и ёмкостного тока, то он имеет величину, изменяющуюся по длине линии.

Плотность тока насыщения

В физической электронике используют понятие плотности тока насыщения. Эта величина характеризует эмиссионную способность металла, из которого сделан катод, и зависит от его вида и температуры.

Плотность тока насыщения выражается формулой, которая была выведена на основе квантовой статистики Ричардсоном и Дешманом:

– плотность тока насыщения[А/м 2 ]

— среднее значение коэффициента отражения электронов от потенциального барьера

— термоэлектрическая постоянная со значением 120,4 А/(K 2 ·см 2 )

— значение работы выхода из катода электронов [эВ],
q
– электронный заряд [Кл]

Понравилась статья, расскажите о ней друзьям:

Источник