Чем обозначается значение функции
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
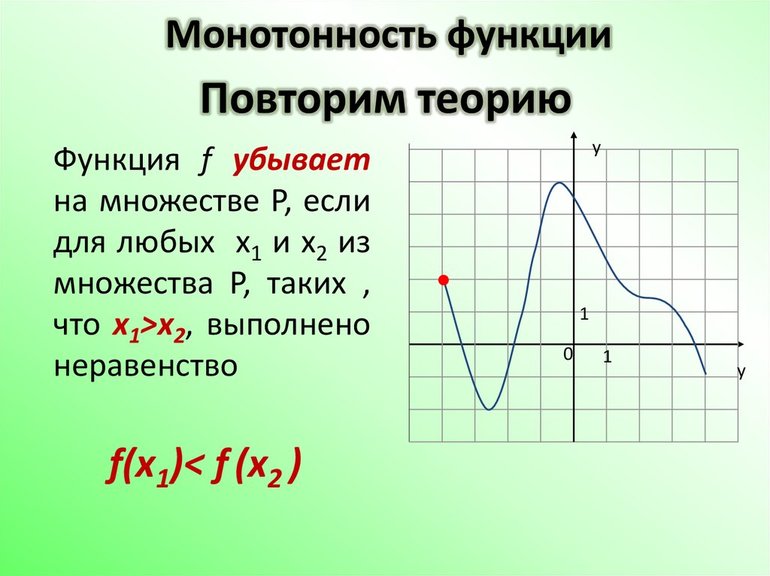
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Основные элементарные функции: их свойства и графики
Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.
Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.
Выделяют следующие виды основных элементарных функций:
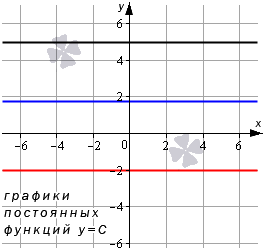
Постоянная функция
Свойства постоянных функций:
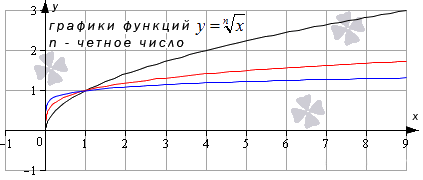
Корень n-й степени
Данная элементарная функция определяется формулой y = x n ( n – натуральное число больше единицы).
Рассмотрим две вариации функции.
Похожий вид у графиков функции четной степени при иных значениях показателя.
Свойства функции корень n-ой степени, n – четное число
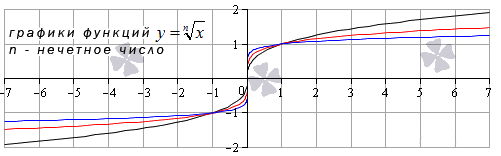
Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида.
Свойства функции корень n-ой степени, n – нечетное число
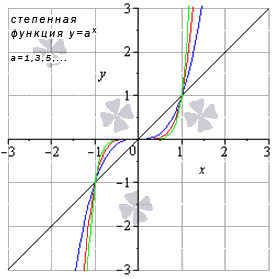
Степенная функция
Вид графиков и свойства функции зависят от значения показателя степени.
Степенная функция при нечетном положительном показателе
Свойства степенной функции, когда показатель степени – нечетный положительный
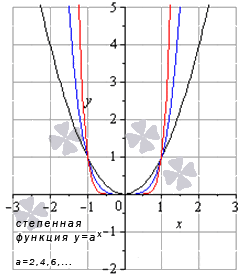
Степенная функция при четном положительном показателе
Свойства степенной функции, когда показатель степени – четный положительный:
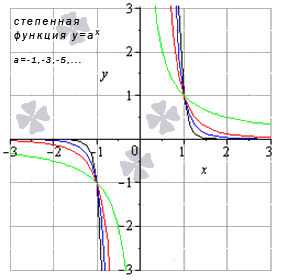
Степенная функция при нечетном отрицательном показателе
Свойства степенной функции, когда показатель степени – нечетный отрицательный:
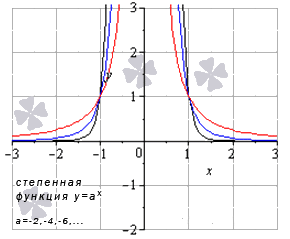
Степенная функция при четном отрицательном показателе степени
Свойства степенной функции, когда показатель степени – четный отрицательный:
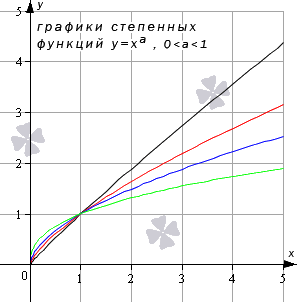
Степенная функция при рациональном или иррациональном показателе (значение больше нуля и меньше единицы)
Иные значения показателя степени a (при условии 0 a 1 ) дадут аналогичный вид графика.
Свойства степенной функции при 0 a 1 :
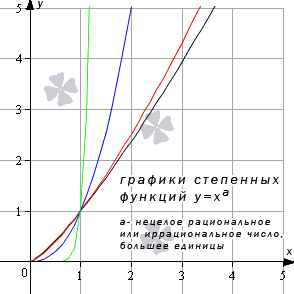
Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)
Иные значения показателя степени а при условии a > 1 дадут похожий вид графика.
Свойства степенной функции при a > 1 :
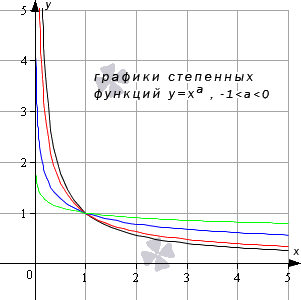
Степенная функция при действительном показателе степени (больше минус единицы и меньше нуля)
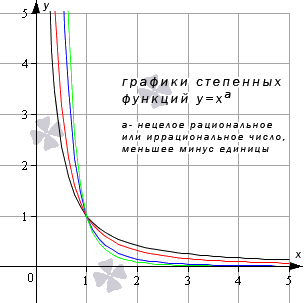
Степенная функция при нецелом действительном показателе степени (меньше минус единицы)
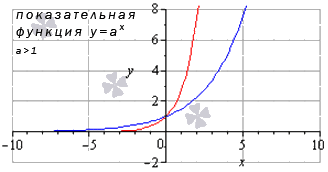
Показательная функция
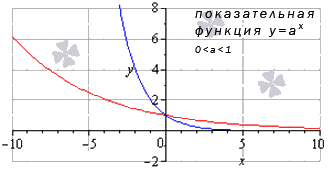
Сначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы ( 0 a 1 ) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).
Свойства показательной функции, когда основание меньше единицы:
Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).
Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции.
Свойства показательной функции, когда основание больше единицы:
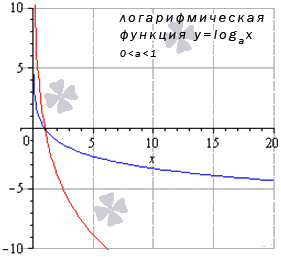
Логарифмическая функция
График логарифмической функции имеет различный вид, исходя из значения основания а.
Иные значения основания, не большие единицы, дадут аналогичный вид графика.
Свойства логарифмической функции, когда основание меньше единицы:
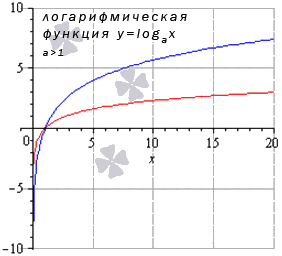
Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже – графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).
Иные значения основания больше единицы дадут аналогичный вид графика.
Свойства логарифмической функции, когда основание больше единицы:
Тригонометрические функции, их свойства и графики
Тригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики.
В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f ( x + T ) = f ( x ) ( T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль.
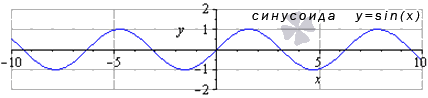
График данной функции называется синусоида.
Свойства функции синус:
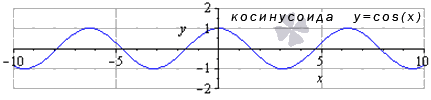
График данной функции называется косинусоида.
Свойства функции косинус:
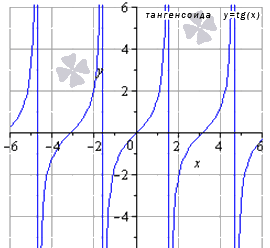
График данной функции называется тангенсоида.
Свойства функции тангенс:
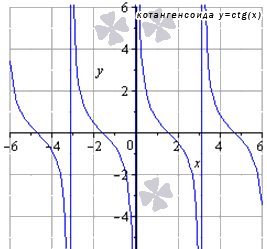
График данной функции называется котангенсоида.
Свойства функции котангенс:
Обратные тригонометрические функции, их свойства и графики
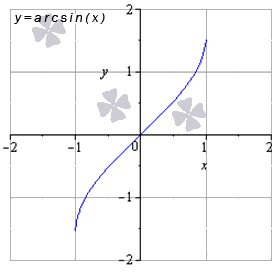
Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.
Свойства функции арксинус:
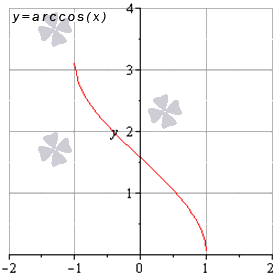
Свойства функции арккосинус:
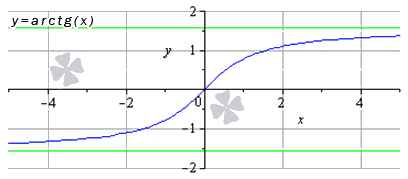
Свойства функции арктангенс:
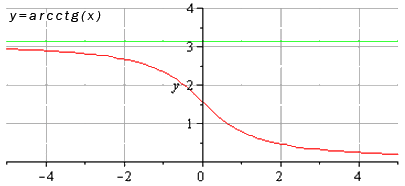
Свойства функции арккотангенс:
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
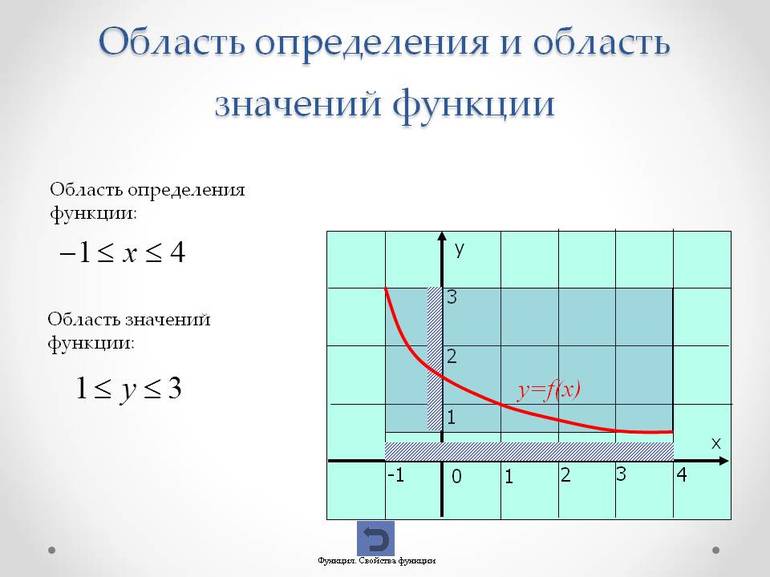
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
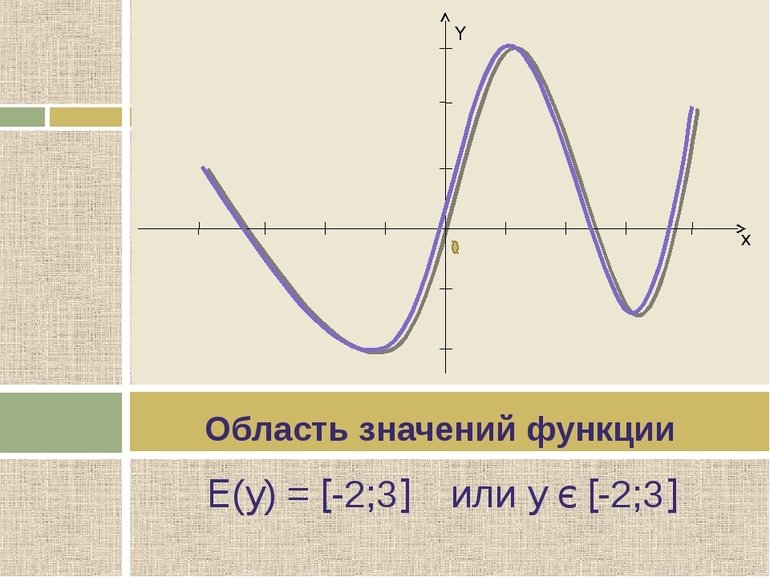
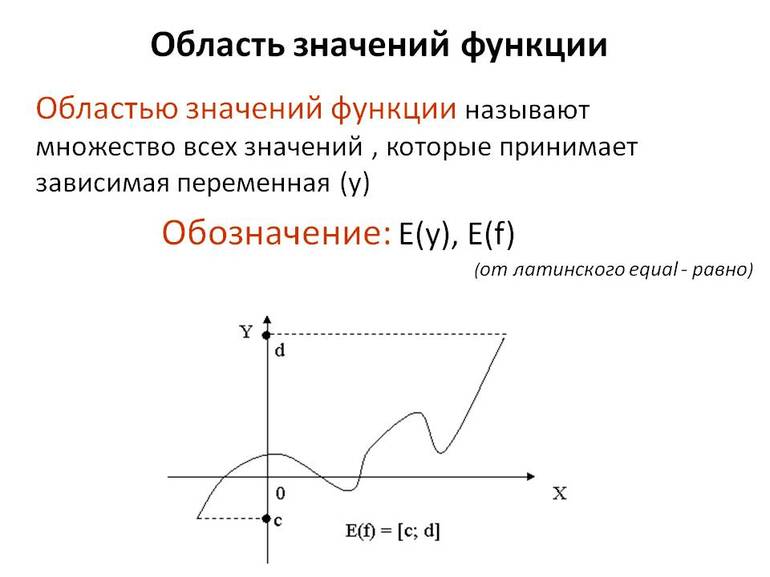
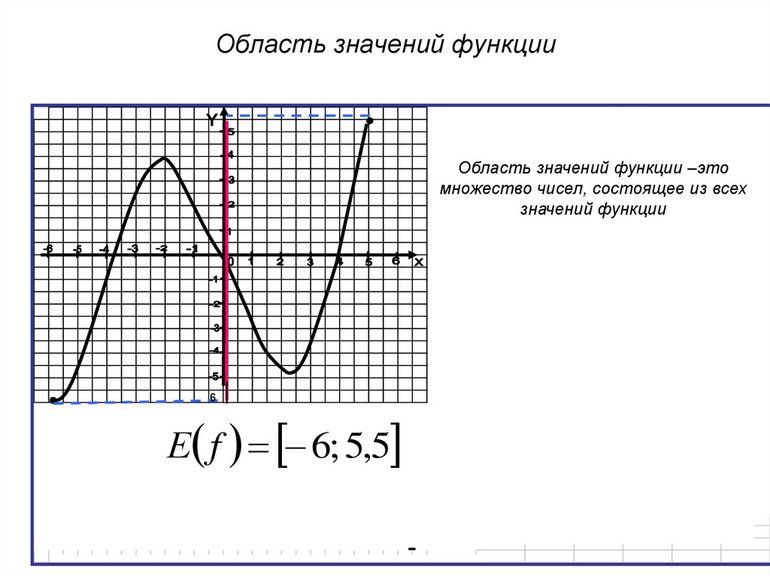
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Общая информация
У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.
Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.
В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.
Основные понятия
Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».
Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.
Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.
Типы функций
Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:
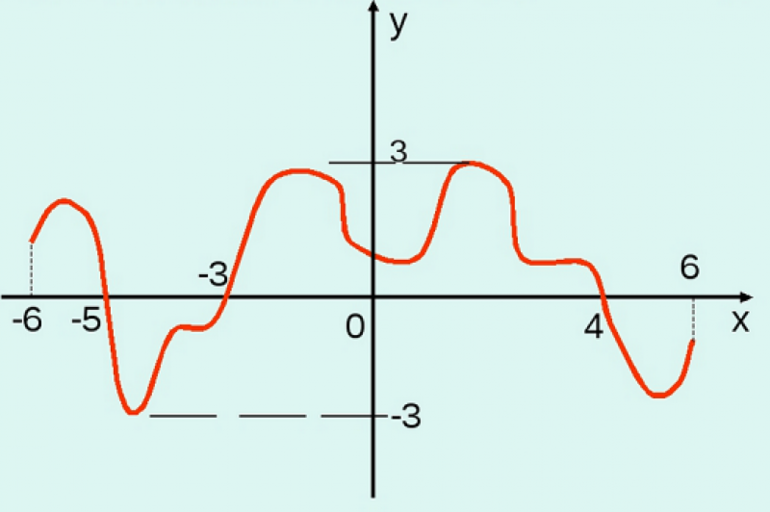
Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.
Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.
Важные свойства
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:
Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.
Методы нахождения
Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:
Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.
Для каждого элемента
Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:
Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:
Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.
Оценочный способ
Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:
Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:
Производная, min и max
Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:
Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:
В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:
Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.
Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.